人教版七年级数学上册3.1.1列方程解应用题-行程问题 课件(共14张PPT)
文档属性
| 名称 | 人教版七年级数学上册3.1.1列方程解应用题-行程问题 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 762.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 13:34:34 | ||
图片预览




文档简介
(共14张PPT)
3.1.1 列一元一次方程解应用题
--------行程问题
温故知新
1. 行程问题的基本等量关系
路程=时间×速度;
时间= 速度=
2. 航行问题中的等量关系:
(1)顺水(风)速度=静水(风)速度____水流(风)速度
(2)逆水(风)速度=静水(风)速度____水流(风)速度
+
-
3. 试一试
(1)小明用了20分钟走了x米,小明的速度是 米/分
(2)甲每小时比乙多走10千米,设乙每小时走x千米,则甲每小时走 千米;
(3)两人登山,甲比乙提前2小时出发,结果两人同时到达山顶,甲用时 x 小时,则乙用时_________.
(x+10)
(x-2)小时
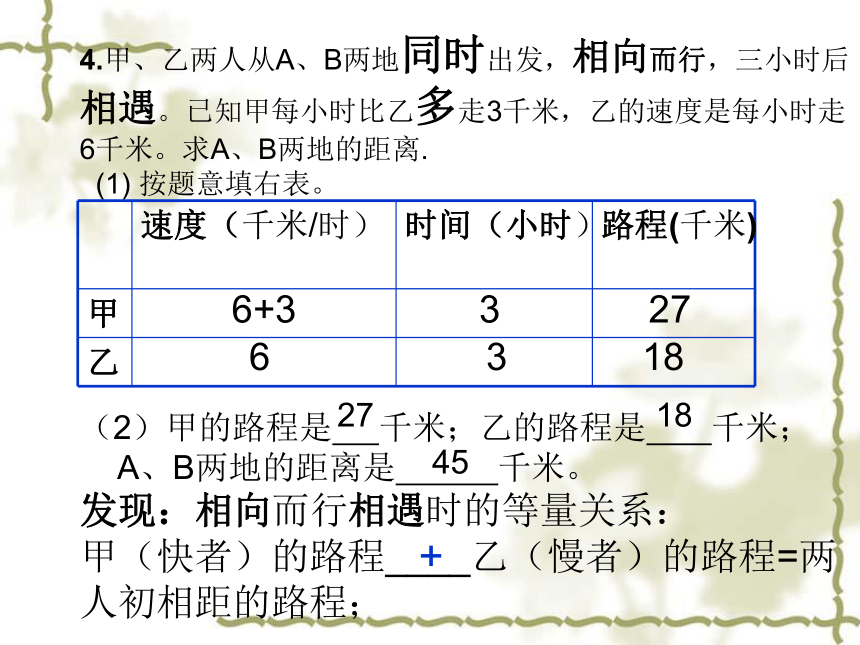
4.甲、乙两人从A、B两地同时出发,相向而行,三小时后相遇。已知甲每小时比乙多走3千米,乙的速度是每小时走6千米。求A、B两地的距离.
(1) 按题意填右表。
(2)甲的路程是 千米;乙的路程是 千米;
A、B两地的距离是 千米。
发现:相向而行相遇时的等量关系:
甲(快者)的路程____乙(慢者)的路程=两人初相距的路程;
速度(千米/时) 时间(小时) 路程(千米)
甲
乙
6+3
6
3
3
27
18
27
18
45
+
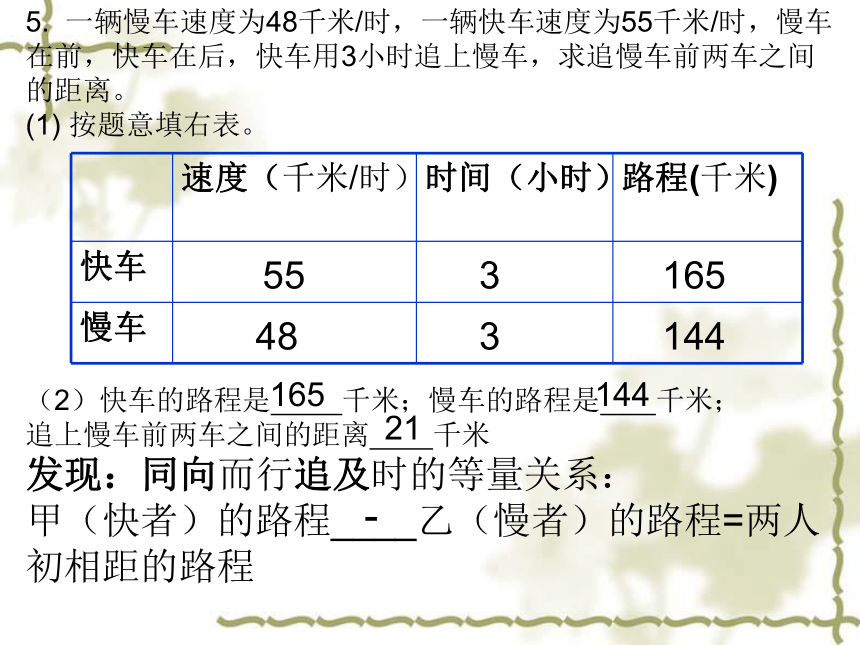
5. 一辆慢车速度为48千米/时,一辆快车速度为55千米/时,慢车在前,快车在后,快车用3小时追上慢车,求追慢车前两车之间的距离。
(1) 按题意填右表。
(2)快车的路程是 千米;慢车的路程是 千米;
追上慢车前两车之间的距离 千米
发现:同向而行追及时的等量关系:
甲(快者)的路程____乙(慢者)的路程=两人初相距的路程
速度(千米/时) 时间(小时) 路程(千米)
快车
慢车
55
48
3
3
165
144
165
144
21
-
例1.甲、乙两人从相距45千米的两地同时出发,相向而 行,三小时后相遇。已知甲每小时比乙多走3千米,求乙的速度。
分析:设乙的速度是 x 千米/时.
等量关系: 的路程 + 的路程=相距路程45千米
解:
速度(千米/时) 时间(小时) 路程(千米)
甲
乙
x
x+3
3
3
3(x+3)
3x
甲
乙
设乙的速度是 x千米/时,列方程:
3(x+3)+3x=45
解得:x=6
答:乙的速度是6千米/时
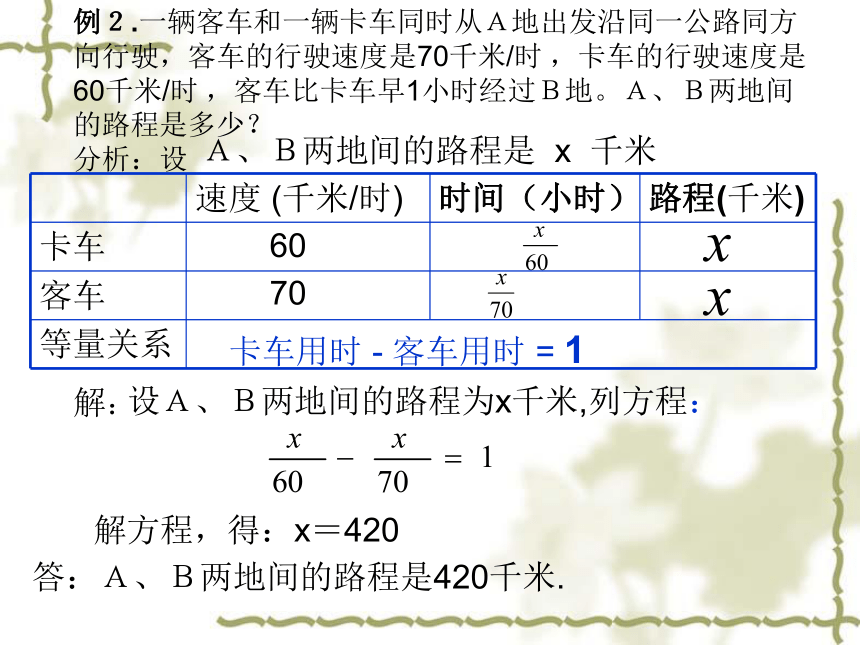
例2.一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70千米/时 ,卡车的行驶速度是60千米/时 ,客车比卡车早1小时经过B地。A、B两地间的路程是多少?
分析:设
解:
速度 (千米/时) 时间(小时) 路程(千米)
卡车
客车
等量关系
60
70
卡车用时 - 客车用时 = 1
设A、B两地间的路程为x千米,列方程:
解方程,得:x=420
答:A、B两地间的路程是420千米.
A、B两地间的路程是 x 千米
速度 (千米/时) 时间(小时) 路程(千米)
卡车
客车
等量关系
60
70
客车行驶路程 = 卡车行驶路程
解:设卡车行驶时间为 x小时,列方程:
答:A、B两地间的路程是420千米.
例2.一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70千米/时 ,卡车的行驶速度是60千米/时 ,客车比卡车早1小时经过B地。A、B两地间的路程是多少?设卡车行驶时间为 x 小时
解方程,得:
路程:
速度 (千米/时) 时间(小时) 路程(千米)
卡车
客车
等量关系
60
70
客车行驶路程 = 卡车行驶路程
解:设客车行驶时间为 x小时,列方程:
答:A、B两地间的路程是420千米.
例2.一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70千米/时 ,卡车的行驶速度是60千米/时 ,客车比卡车早1小时经过B地。A、B两地间的路程是多少?设客车行驶时间为 x 小时
二、课堂练习
1.一辆慢车速度为48千米/时,一辆快车速度为55千米/时,慢车在前,快车在后,两车之间的距离为21千米,快车追上慢车需要多少小时?
分析:设
快车追上慢车需要x小时
时间(小时))
慢车
快车
等量关系:快车的路程____慢车的路程=21.
可列方程为:
速度(千米/时)
路程(千米)
48
-
55
x
x
48 x
55 x
55 x - 48 x = 21
2.轮船在两码头之间航行,顺水航行需要1小时40分,逆水航行需3小时,水流的速度是12千米/时。求轮船在静水中的速度?
轮船在静水中的速度为 x 千米/时
顺水
逆水
顺水航行的路程 =逆水航行的路程
可列方程为:
速度(千米/时)
时间(小时)
路程(千米)
X+12
X-12
3
3(x-12)
等量关系:
分析:设
分析:设
3.甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
甲
乙
速度(千米/时)
时间(小时)
路程(千米)
甲经过 秒可以追上乙
7
6.5
3.甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
解:设甲经过x秒可以追上乙,列方程得:
7x = 6.5(x+1)
解得: x=13
答:甲经过13秒可以追上乙
小结:1.列方程解应用题的步骤:①设元;②列方程;
③解方程;④答数
2.行程问题(相遇问题)中常见的等量关系
(1)相向而行相遇时的等量关系:
快者的路程____慢者的路程=两人初相距的路程
(2)同向而行追及时的等量关系:
快者的路程____慢者的路程=两人初相距的路程.
+
-
反馈案
A组
1.张华和李明同时登一座山,张华每分钟登高10,李明每分钟登高15,结果李明比张华早30分钟到达山顶,求山高.
2..两辆汽车从相距84km的两地同时出发相向而行,甲车的速度比乙车的速度快20km/h,半小时后两车相遇,两车多速度各是多少?
3.在风速为24km/h的条件下,一架飞机顺风从A机场飞到B机场要用2.8小时,它逆风飞行同样多航线要用3小时。求(1)无风时这架飞机在这一航线的平均航速;(2)两机场之间多航程。
B组
4.运动场的跑道一圈长400m,小健练习骑自行车,平均每分钟骑350m;小康练习跑步,平均每分钟跑250m,两人从同一处同时反向出发,经过多少时间首次相遇?又经过多少时间再次相遇?
3.1.1 列一元一次方程解应用题
--------行程问题
温故知新
1. 行程问题的基本等量关系
路程=时间×速度;
时间= 速度=
2. 航行问题中的等量关系:
(1)顺水(风)速度=静水(风)速度____水流(风)速度
(2)逆水(风)速度=静水(风)速度____水流(风)速度
+
-
3. 试一试
(1)小明用了20分钟走了x米,小明的速度是 米/分
(2)甲每小时比乙多走10千米,设乙每小时走x千米,则甲每小时走 千米;
(3)两人登山,甲比乙提前2小时出发,结果两人同时到达山顶,甲用时 x 小时,则乙用时_________.
(x+10)
(x-2)小时
4.甲、乙两人从A、B两地同时出发,相向而行,三小时后相遇。已知甲每小时比乙多走3千米,乙的速度是每小时走6千米。求A、B两地的距离.
(1) 按题意填右表。
(2)甲的路程是 千米;乙的路程是 千米;
A、B两地的距离是 千米。
发现:相向而行相遇时的等量关系:
甲(快者)的路程____乙(慢者)的路程=两人初相距的路程;
速度(千米/时) 时间(小时) 路程(千米)
甲
乙
6+3
6
3
3
27
18
27
18
45
+
5. 一辆慢车速度为48千米/时,一辆快车速度为55千米/时,慢车在前,快车在后,快车用3小时追上慢车,求追慢车前两车之间的距离。
(1) 按题意填右表。
(2)快车的路程是 千米;慢车的路程是 千米;
追上慢车前两车之间的距离 千米
发现:同向而行追及时的等量关系:
甲(快者)的路程____乙(慢者)的路程=两人初相距的路程
速度(千米/时) 时间(小时) 路程(千米)
快车
慢车
55
48
3
3
165
144
165
144
21
-
例1.甲、乙两人从相距45千米的两地同时出发,相向而 行,三小时后相遇。已知甲每小时比乙多走3千米,求乙的速度。
分析:设乙的速度是 x 千米/时.
等量关系: 的路程 + 的路程=相距路程45千米
解:
速度(千米/时) 时间(小时) 路程(千米)
甲
乙
x
x+3
3
3
3(x+3)
3x
甲
乙
设乙的速度是 x千米/时,列方程:
3(x+3)+3x=45
解得:x=6
答:乙的速度是6千米/时
例2.一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70千米/时 ,卡车的行驶速度是60千米/时 ,客车比卡车早1小时经过B地。A、B两地间的路程是多少?
分析:设
解:
速度 (千米/时) 时间(小时) 路程(千米)
卡车
客车
等量关系
60
70
卡车用时 - 客车用时 = 1
设A、B两地间的路程为x千米,列方程:
解方程,得:x=420
答:A、B两地间的路程是420千米.
A、B两地间的路程是 x 千米
速度 (千米/时) 时间(小时) 路程(千米)
卡车
客车
等量关系
60
70
客车行驶路程 = 卡车行驶路程
解:设卡车行驶时间为 x小时,列方程:
答:A、B两地间的路程是420千米.
例2.一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70千米/时 ,卡车的行驶速度是60千米/时 ,客车比卡车早1小时经过B地。A、B两地间的路程是多少?设卡车行驶时间为 x 小时
解方程,得:
路程:
速度 (千米/时) 时间(小时) 路程(千米)
卡车
客车
等量关系
60
70
客车行驶路程 = 卡车行驶路程
解:设客车行驶时间为 x小时,列方程:
答:A、B两地间的路程是420千米.
例2.一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70千米/时 ,卡车的行驶速度是60千米/时 ,客车比卡车早1小时经过B地。A、B两地间的路程是多少?设客车行驶时间为 x 小时
二、课堂练习
1.一辆慢车速度为48千米/时,一辆快车速度为55千米/时,慢车在前,快车在后,两车之间的距离为21千米,快车追上慢车需要多少小时?
分析:设
快车追上慢车需要x小时
时间(小时))
慢车
快车
等量关系:快车的路程____慢车的路程=21.
可列方程为:
速度(千米/时)
路程(千米)
48
-
55
x
x
48 x
55 x
55 x - 48 x = 21
2.轮船在两码头之间航行,顺水航行需要1小时40分,逆水航行需3小时,水流的速度是12千米/时。求轮船在静水中的速度?
轮船在静水中的速度为 x 千米/时
顺水
逆水
顺水航行的路程 =逆水航行的路程
可列方程为:
速度(千米/时)
时间(小时)
路程(千米)
X+12
X-12
3
3(x-12)
等量关系:
分析:设
分析:设
3.甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
甲
乙
速度(千米/时)
时间(小时)
路程(千米)
甲经过 秒可以追上乙
7
6.5
3.甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
解:设甲经过x秒可以追上乙,列方程得:
7x = 6.5(x+1)
解得: x=13
答:甲经过13秒可以追上乙
小结:1.列方程解应用题的步骤:①设元;②列方程;
③解方程;④答数
2.行程问题(相遇问题)中常见的等量关系
(1)相向而行相遇时的等量关系:
快者的路程____慢者的路程=两人初相距的路程
(2)同向而行追及时的等量关系:
快者的路程____慢者的路程=两人初相距的路程.
+
-
反馈案
A组
1.张华和李明同时登一座山,张华每分钟登高10,李明每分钟登高15,结果李明比张华早30分钟到达山顶,求山高.
2..两辆汽车从相距84km的两地同时出发相向而行,甲车的速度比乙车的速度快20km/h,半小时后两车相遇,两车多速度各是多少?
3.在风速为24km/h的条件下,一架飞机顺风从A机场飞到B机场要用2.8小时,它逆风飞行同样多航线要用3小时。求(1)无风时这架飞机在这一航线的平均航速;(2)两机场之间多航程。
B组
4.运动场的跑道一圈长400m,小健练习骑自行车,平均每分钟骑350m;小康练习跑步,平均每分钟跑250m,两人从同一处同时反向出发,经过多少时间首次相遇?又经过多少时间再次相遇?
