人教版七年级数学上册1.2.3相反数 课件(共22张PPT)
文档属性
| 名称 | 人教版七年级数学上册1.2.3相反数 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 566.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
课程名称:1.2.3相反数
学科:中学数学 人教版 七年级 上册
1、数轴:
规定了原点、
正方向
和单位长度的直线.
知识回顾
2、数轴三要素
2、数轴三要素
原点
正方向
单位长度
知识回顾
3、观察如图所示的数轴,回答下列问题。
5
4
3
2
1
0
-1
-2
-3
-4
D
B
A
C
(1)说出数轴上的点A,B,C,D表示的有理数
两侧
对称
(2)数轴上表示-1和1的点分别在原点的 ,关于原点 ,并且到原点的距离都等于
1个单位长度。
(3)数轴上表示-3和3的点分别在原点的 ,关于原点 ,并且到原点的距离都等于
两侧
3个单位长度。
对称
学习目标:
1、借助数轴了解相反数的概念,知道互为相反数的两个数之间的位置关系;
2、能求一个数的相反数;
3、理解和掌握双重符号的化简。
(重点)
(重点)
(难点)
1、数轴上与原点的距离是2的点有____个,这些点表示的数是_______ ;
2、数轴上与原点的距离是5的点有____ 个, 这些点表示的数是_______ ;
3、数轴上与原点的距离是10的点有___ 个, 这些点表示的数是__________ ;
2
+2或-2
+5或-5
2
2
+10或-10
一般地,设a是一个正数,数轴上与原点的距离是a的点有 ,它们分别在原点的 ,表示 ,我们说这两点关于原点对称。
两个
左右
-a和a
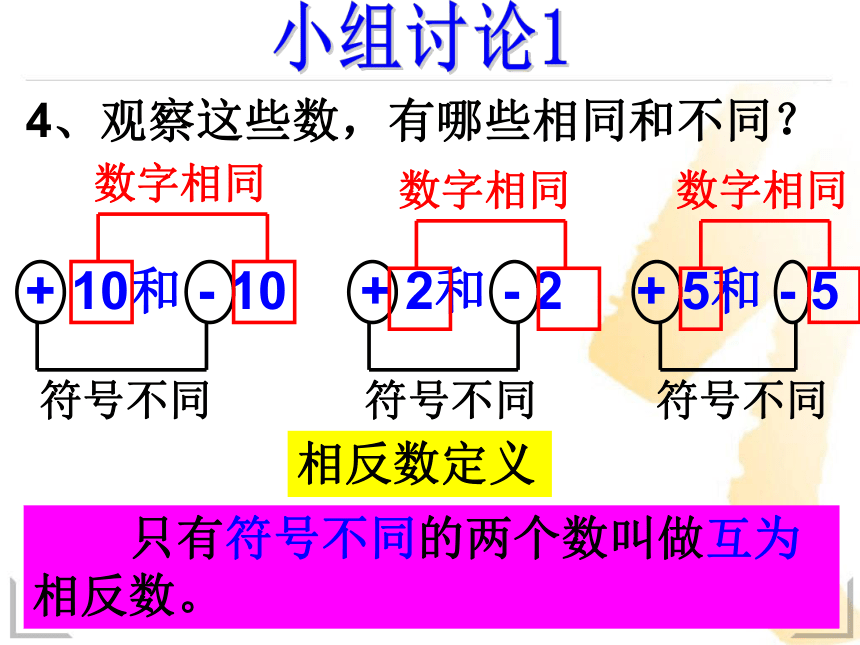
+ 10和 - 10 + 2和 - 2 + 5和 - 5
符号不同
符号不同
符号不同
数字相同
数字相同
数字相同
4、观察这些数,有哪些相同和不同?
相反数定义
只有符号不同的两个数叫做互为相反数。
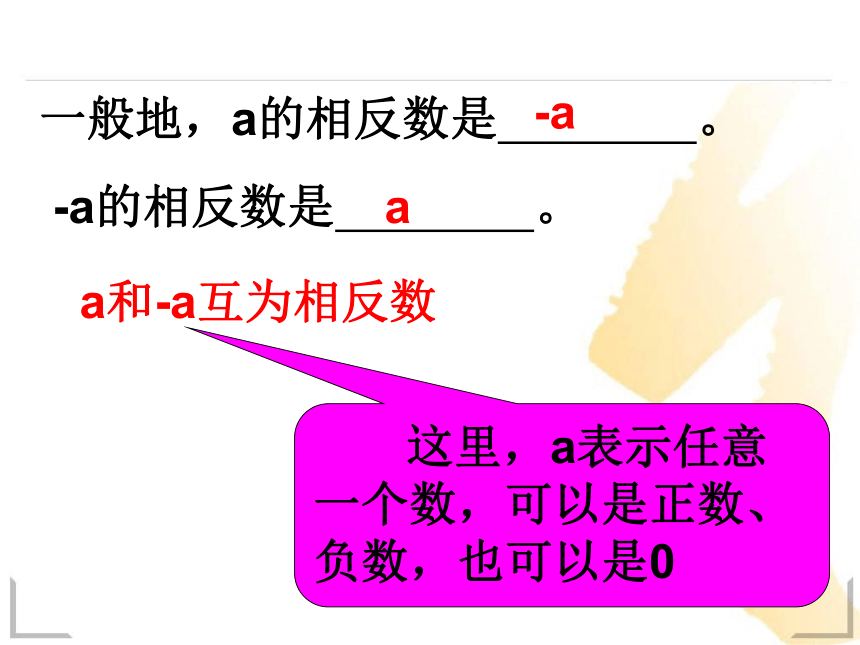
一般地,a的相反数是 。
-a的相反数是 。
-a
a
a和-a互为相反数
这里,a表示任意一个数,可以是正数、负数,也可以是0
概念的理解
判断:
(1)-3和+3都是相反数 ( )
(2)-3是3的相反数( )
(3)-3与+3互为相反数( )
(4)+3是-3的相反数( )
√
√
×
√
(-9,7,0, 0.2)
( 2.4,1.7,-1)
1.分别说出9,-7,0,-0.2的相反数.
2.指出-2.4,-1.7,1各是什么数的相反数?
试一试
0
1
3
-3
7.5
-4.8
E
D
O
A
B
C
2、D,B两点分别在原点的左边和右边,它们还有什么特殊的关系?
到原点的距离都等于3
1、这个图中的点所代表的数中,有没有关系特殊的数呢?
3、数轴上表示相反数的两个点和原点有什么关系?
在数轴上表示互为相反数的两个数的点,分别位于原点的两侧,且到原点的距离相等,这两点关于原点对称 。
(小组讨论2)
思考:如何求一个数的相反数?
8的相反数是 ,
7的相反数是 ,
5的相反数是 。
由此可知,求一个数的相反数就是在这个数的前面添上“-”号
-8
-7
-5
(1)如-5的相反数,可以表示为 。
-(-5)
如+6的相反数,可以表示为 。
-(+6)
(2)a-4的相反数是 ,
-(a-4)
3-x的相反数是 ,
-(3-x)
请说出下列各式表示的含义及其结果:
-(+1.1)表示什么呢?
-(-7)表示什么呢?
-1.1
7
-3.8
(正数的相反数是 )
(负数的相反数是 )
+(-3.8)表示什么呢?
(负数的本身是 )
-0表示什么呢?
0
(0的相反数是 )
负数
正数
负数
0
你发现了括号内外的符号“联手”对结果符号的影响吗?说说你的发现
(3)+(-5)=
(4)-(+4.3)=
(1)+(+2)=
-5
-4.3
2
1
-1
-1
(2)-(-3)=
3
1、简化符号时,同号得正,异号得负;
2、出现多重符号时看“-”的个数。当“-”是奇数个时,结果为 ;当“-”是偶数个时,结果为 。
负
正
(7)+﹝+(-1)﹞=
(5)-﹝-(+1)﹞=
(6)-﹝-(-1)﹞=
同步练习
化简下列各数的符号
课堂小结
学习目标:
1、借助数轴了解相反数的概念,知道互为相反数的两个数之间的位置关系;
2、能求一个数的相反数;
3、理解和掌握双重符号的化简。
(重点)
(重点)
(难点)
作业
教科书P10页 练习:第2题,第4题
教科书P14页 习题1.2:第4题
当堂检测
1、下列几组数中互为相反数的是( )
A.- 和0.7 B. 和-0.333
1
7
1
3
C.- (-6)和6 D. - 和0.25
1
4
D
2、下列化简错误的是( )
A.- (-3)=3 B. +(-3)=-3
C.- 〔+(-3)〕=-3 D. -〔-(-3)〕=-3
C
当堂检测
3、如a=+2.5,那么-a= ;
4、如果a的相反数是-5,b的相反数是它本身,那么a+b= 。
如-a=-4,那么a= ;
-2.5
4
5
√
×
√
×
(4)a的相反数是-a,-a一定是负数。( )
(3)-0.2是相反数。( )
(2)在数轴上,互为相反数的两个数到原点 的距离相等。( )
5、判断:
(1)正数的相反数一定是负数。( )
结束寄语
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现。
下课了!
6、化简下列各数的符号
当堂检测
7、已知在数轴上有表示互为相反数的两个点A、B,它们间的距离是6,若用a、b(a>b)来表示这两个数,求a、b.
解:
A、B两点到原点的距离是
6÷2=3,
∵a>b
∴a=3,
b=-3.
当堂检测
课程名称:1.2.3相反数
学科:中学数学 人教版 七年级 上册
1、数轴:
规定了原点、
正方向
和单位长度的直线.
知识回顾
2、数轴三要素
2、数轴三要素
原点
正方向
单位长度
知识回顾
3、观察如图所示的数轴,回答下列问题。
5
4
3
2
1
0
-1
-2
-3
-4
D
B
A
C
(1)说出数轴上的点A,B,C,D表示的有理数
两侧
对称
(2)数轴上表示-1和1的点分别在原点的 ,关于原点 ,并且到原点的距离都等于
1个单位长度。
(3)数轴上表示-3和3的点分别在原点的 ,关于原点 ,并且到原点的距离都等于
两侧
3个单位长度。
对称
学习目标:
1、借助数轴了解相反数的概念,知道互为相反数的两个数之间的位置关系;
2、能求一个数的相反数;
3、理解和掌握双重符号的化简。
(重点)
(重点)
(难点)
1、数轴上与原点的距离是2的点有____个,这些点表示的数是_______ ;
2、数轴上与原点的距离是5的点有____ 个, 这些点表示的数是_______ ;
3、数轴上与原点的距离是10的点有___ 个, 这些点表示的数是__________ ;
2
+2或-2
+5或-5
2
2
+10或-10
一般地,设a是一个正数,数轴上与原点的距离是a的点有 ,它们分别在原点的 ,表示 ,我们说这两点关于原点对称。
两个
左右
-a和a
+ 10和 - 10 + 2和 - 2 + 5和 - 5
符号不同
符号不同
符号不同
数字相同
数字相同
数字相同
4、观察这些数,有哪些相同和不同?
相反数定义
只有符号不同的两个数叫做互为相反数。
一般地,a的相反数是 。
-a的相反数是 。
-a
a
a和-a互为相反数
这里,a表示任意一个数,可以是正数、负数,也可以是0
概念的理解
判断:
(1)-3和+3都是相反数 ( )
(2)-3是3的相反数( )
(3)-3与+3互为相反数( )
(4)+3是-3的相反数( )
√
√
×
√
(-9,7,0, 0.2)
( 2.4,1.7,-1)
1.分别说出9,-7,0,-0.2的相反数.
2.指出-2.4,-1.7,1各是什么数的相反数?
试一试
0
1
3
-3
7.5
-4.8
E
D
O
A
B
C
2、D,B两点分别在原点的左边和右边,它们还有什么特殊的关系?
到原点的距离都等于3
1、这个图中的点所代表的数中,有没有关系特殊的数呢?
3、数轴上表示相反数的两个点和原点有什么关系?
在数轴上表示互为相反数的两个数的点,分别位于原点的两侧,且到原点的距离相等,这两点关于原点对称 。
(小组讨论2)
思考:如何求一个数的相反数?
8的相反数是 ,
7的相反数是 ,
5的相反数是 。
由此可知,求一个数的相反数就是在这个数的前面添上“-”号
-8
-7
-5
(1)如-5的相反数,可以表示为 。
-(-5)
如+6的相反数,可以表示为 。
-(+6)
(2)a-4的相反数是 ,
-(a-4)
3-x的相反数是 ,
-(3-x)
请说出下列各式表示的含义及其结果:
-(+1.1)表示什么呢?
-(-7)表示什么呢?
-1.1
7
-3.8
(正数的相反数是 )
(负数的相反数是 )
+(-3.8)表示什么呢?
(负数的本身是 )
-0表示什么呢?
0
(0的相反数是 )
负数
正数
负数
0
你发现了括号内外的符号“联手”对结果符号的影响吗?说说你的发现
(3)+(-5)=
(4)-(+4.3)=
(1)+(+2)=
-5
-4.3
2
1
-1
-1
(2)-(-3)=
3
1、简化符号时,同号得正,异号得负;
2、出现多重符号时看“-”的个数。当“-”是奇数个时,结果为 ;当“-”是偶数个时,结果为 。
负
正
(7)+﹝+(-1)﹞=
(5)-﹝-(+1)﹞=
(6)-﹝-(-1)﹞=
同步练习
化简下列各数的符号
课堂小结
学习目标:
1、借助数轴了解相反数的概念,知道互为相反数的两个数之间的位置关系;
2、能求一个数的相反数;
3、理解和掌握双重符号的化简。
(重点)
(重点)
(难点)
作业
教科书P10页 练习:第2题,第4题
教科书P14页 习题1.2:第4题
当堂检测
1、下列几组数中互为相反数的是( )
A.- 和0.7 B. 和-0.333
1
7
1
3
C.- (-6)和6 D. - 和0.25
1
4
D
2、下列化简错误的是( )
A.- (-3)=3 B. +(-3)=-3
C.- 〔+(-3)〕=-3 D. -〔-(-3)〕=-3
C
当堂检测
3、如a=+2.5,那么-a= ;
4、如果a的相反数是-5,b的相反数是它本身,那么a+b= 。
如-a=-4,那么a= ;
-2.5
4
5
√
×
√
×
(4)a的相反数是-a,-a一定是负数。( )
(3)-0.2是相反数。( )
(2)在数轴上,互为相反数的两个数到原点 的距离相等。( )
5、判断:
(1)正数的相反数一定是负数。( )
结束寄语
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现。
下课了!
6、化简下列各数的符号
当堂检测
7、已知在数轴上有表示互为相反数的两个点A、B,它们间的距离是6,若用a、b(a>b)来表示这两个数,求a、b.
解:
A、B两点到原点的距离是
6÷2=3,
∵a>b
∴a=3,
b=-3.
当堂检测
