2021—2022学年苏科版数学九年级下册 第7章 锐角三角函数 综合能力检测题 (word版、含答案)
文档属性
| 名称 | 2021—2022学年苏科版数学九年级下册 第7章 锐角三角函数 综合能力检测题 (word版、含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 184.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 00:00:00 | ||
图片预览

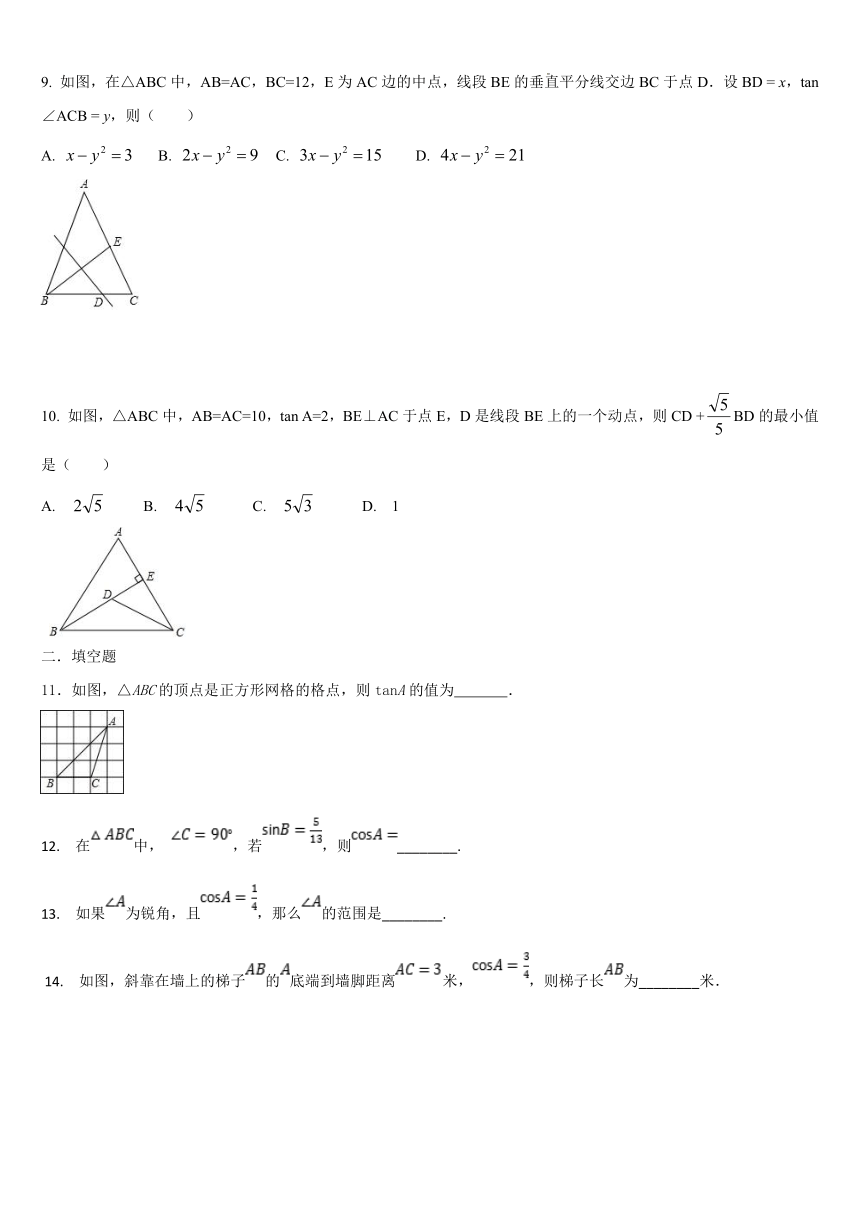
文档简介
《锐角三角函数》综合能力检测题
一.选择题
1.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列等式中,正确的是( )
A. B. C. D.
2.若∠A为锐角,且2cosA<,则∠A( )
A.小于30° B.大于30°
C.大于45°且小于60° D.大于60°
3.在Rt△ABC中,∠C=90°,已知tanA=,那么cosA的值是( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,若m=sinA+sinB,则( )
A.0<m<1 B.0<m≤1 C.m≥1 D.1<m<2
5. 已知为锐角,,则=( )
A. B. C. D.
6. 在中,,下列式子中不一定成立的是( )
A. B.
C. D.
7. 已知:在中,,,则的值为( )
A. B. C. D.
8. 如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )
A.(60+100sinα)cm B.(60+100cosα)cm
C.(60+100tanα)cm D.以上答案都不对
9. 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD = x,tan∠ACB = y,则( )
A. B. C. D.
10. 如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD +BD的最小值是( )
A. B. C. D. 1
二.填空题
11.如图,△ABC的顶点是正方形网格的格点,则tanA的值为 .
12. 在中, ,若,则________.
13. 如果为锐角,且,那么的范围是________.
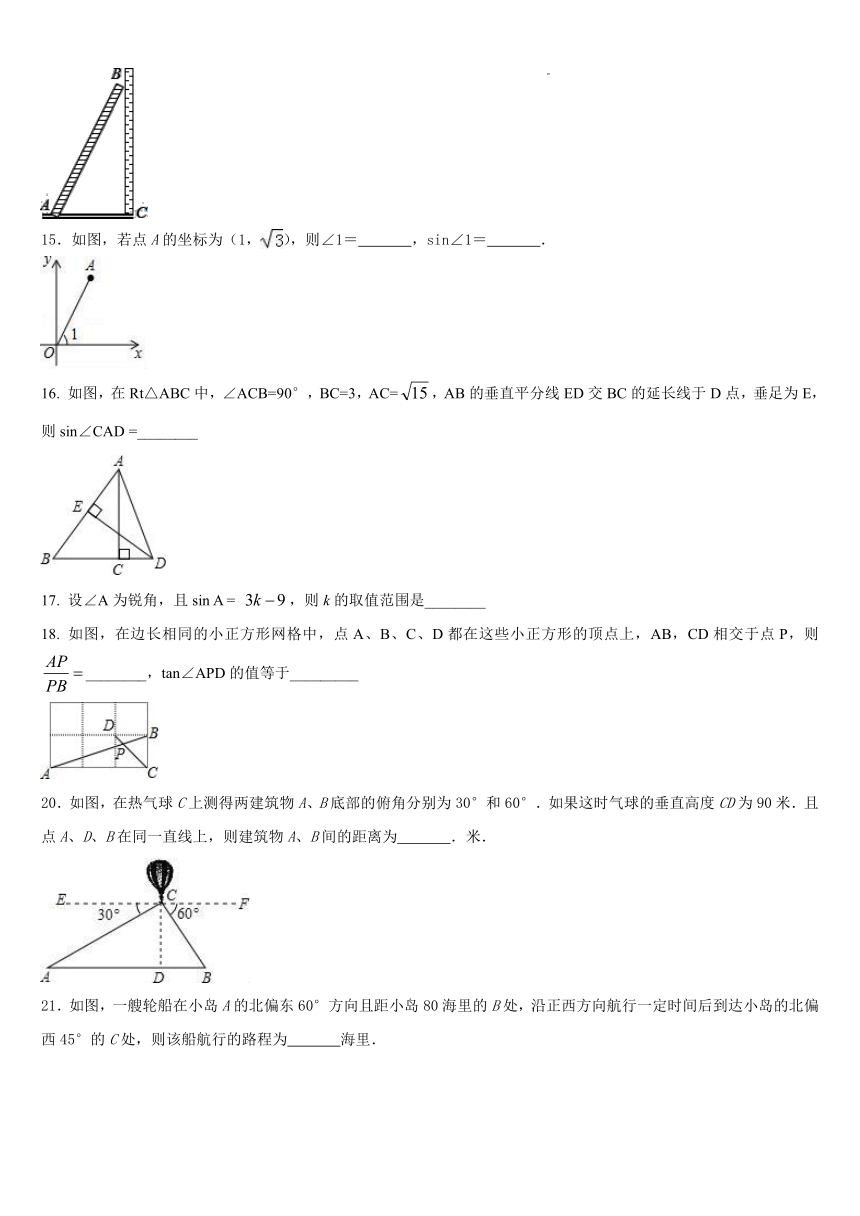
14. 如图,斜靠在墙上的梯子的底端到墙脚距离米,,则梯子长为________米.
15.如图,若点A的坐标为(1,),则∠1= ,sin∠1= .
16. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD =________
17. 设∠A为锐角,且sin A = ,则k的取值范围是________
18. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则________,tan∠APD的值等于_________
20.如图,在热气球C上测得两建筑物A、B底部的俯角分别为30°和60°.如果这时气球的垂直高度CD为90米.且点A、D、B在同一直线上,则建筑物A、B间的距离为 .米.
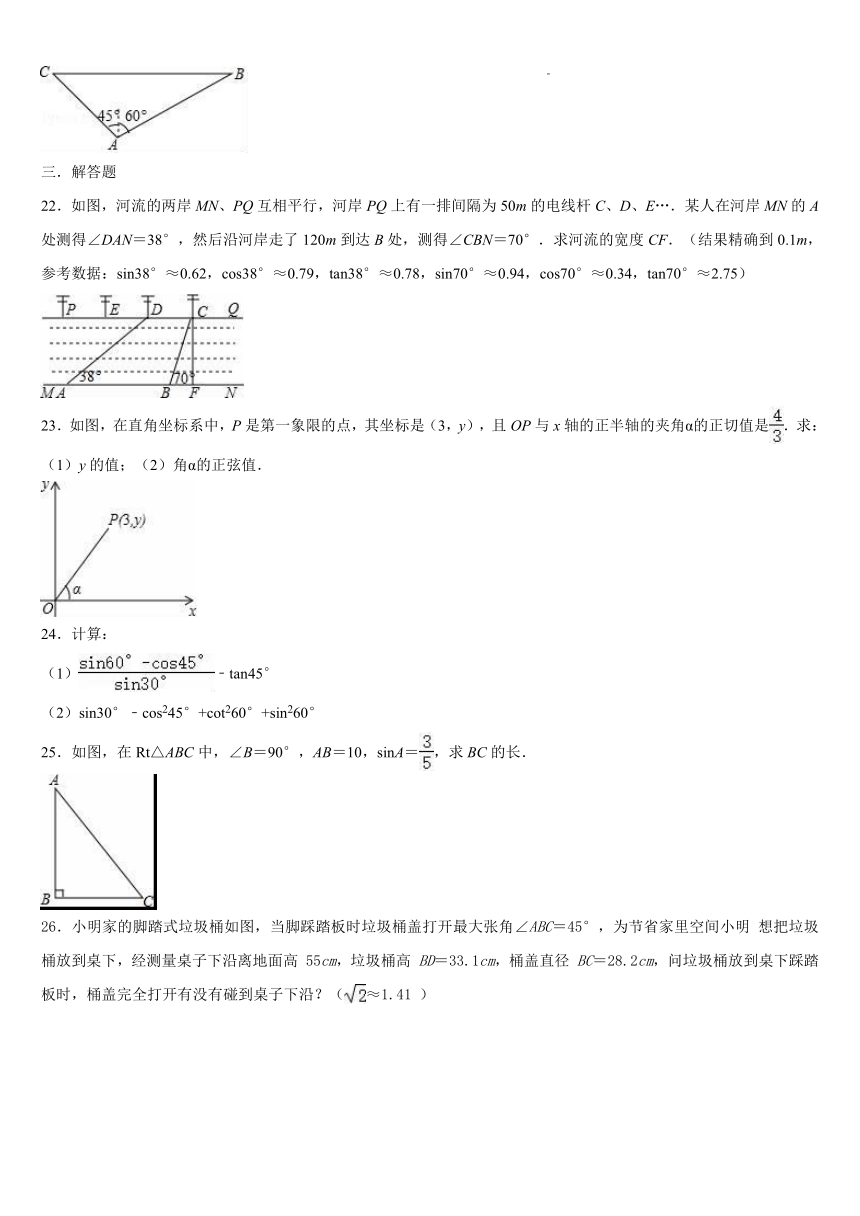
21.如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为 海里.
三.解答题
22.如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E….某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120m到达B处,测得∠CBN=70°.求河流的宽度CF.(结果精确到0.1m,参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
23.如图,在直角坐标系中,P是第一象限的点,其坐标是(3,y),且OP与x轴的正半轴的夹角α的正切值是.求:(1)y的值;(2)角α的正弦值.
24.计算:
(1)﹣tan45°
(2)sin30°﹣cos245°+cot260°+sin260°
25.如图,在Rt△ABC中,∠B=90°,AB=10,sinA=,求BC的长.
26.小明家的脚踏式垃圾桶如图,当脚踩踏板时垃圾桶盖打开最大张角∠ABC=45°,为节省家里空间小明 想把垃圾桶放到桌下,经测量桌子下沿离地面高 55cm,垃圾桶高 BD=33.1cm,桶盖直径 BC=28.2cm,问垃圾桶放到桌下踩踏板时,桶盖完全打开有没有碰到桌子下沿?(≈1.41 )
参考答案
1. C 2. B 3.D 4.D 5.D 6. D 7.B 8. A 9. B 10. B
11..
12..
13..
14.
15.60°、.
16.
17.
18. 3 2
19.30°.
20.120.
21.(40+40)海里.
22.解:过点C作CG∥DA交AB于点G.
∵MN∥PQ,CG∥DA,
∴四边形AGCD是平行四边形.
∴AG=CD=50m,∠CGB=38°.
∴GB=AB﹣AG=120﹣50=70(m).
∴tan38°==0.78,
在Rt△BFC中,
tan70°==2.75,
∴BF=,
∴==0.78,
解得:CF≈76.2(m).
答:河流的宽是76.2米.
23.解:作PC⊥x轴于C.
∵tanα=,OC=3,
∴PC=4,即y=4.
则OP=5.
则sinα=.
24.解:(1)原式=﹣1=﹣1,
(2)原式=++=.
25.解:如图,∵在Rt△ABC中,∠B=90°,AB=10,sinA=,
∴=,
则AC=BC.
又由勾股定理得到:AB2+BC2=AC2,即102+BC2=BC2,
∴BC=7.5.
26解:过点C作CG⊥DE交AB于H.
由题意得:四边形ABDE是矩形,
∴AB∥DE,
∴∠CHB=90°,CH=BD=33.1,
在Rt△CBH中,sin∠CBH=,
∴CH=BC sin∠CBH=28.2×≈20,
∴CG=CH+HG=33.1+20=53.1<55,
答:桶盖完全打开时没有碰到碰到子下沿.
一.选择题
1.在Rt△ABC中,∠C=90°,a、b、c分别是∠A、∠B、∠C的对边,下列等式中,正确的是( )
A. B. C. D.
2.若∠A为锐角,且2cosA<,则∠A( )
A.小于30° B.大于30°
C.大于45°且小于60° D.大于60°
3.在Rt△ABC中,∠C=90°,已知tanA=,那么cosA的值是( )
A. B. C. D.
4.在Rt△ABC中,∠C=90°,若m=sinA+sinB,则( )
A.0<m<1 B.0<m≤1 C.m≥1 D.1<m<2
5. 已知为锐角,,则=( )
A. B. C. D.
6. 在中,,下列式子中不一定成立的是( )
A. B.
C. D.
7. 已知:在中,,,则的值为( )
A. B. C. D.
8. 如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是( )
A.(60+100sinα)cm B.(60+100cosα)cm
C.(60+100tanα)cm D.以上答案都不对
9. 如图,在△ABC中,AB=AC,BC=12,E为AC边的中点,线段BE的垂直平分线交边BC于点D.设BD = x,tan∠ACB = y,则( )
A. B. C. D.
10. 如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD +BD的最小值是( )
A. B. C. D. 1
二.填空题
11.如图,△ABC的顶点是正方形网格的格点,则tanA的值为 .
12. 在中, ,若,则________.
13. 如果为锐角,且,那么的范围是________.
14. 如图,斜靠在墙上的梯子的底端到墙脚距离米,,则梯子长为________米.
15.如图,若点A的坐标为(1,),则∠1= ,sin∠1= .
16. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD =________
17. 设∠A为锐角,且sin A = ,则k的取值范围是________
18. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则________,tan∠APD的值等于_________
20.如图,在热气球C上测得两建筑物A、B底部的俯角分别为30°和60°.如果这时气球的垂直高度CD为90米.且点A、D、B在同一直线上,则建筑物A、B间的距离为 .米.
21.如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为 海里.
三.解答题
22.如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E….某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120m到达B处,测得∠CBN=70°.求河流的宽度CF.(结果精确到0.1m,参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
23.如图,在直角坐标系中,P是第一象限的点,其坐标是(3,y),且OP与x轴的正半轴的夹角α的正切值是.求:(1)y的值;(2)角α的正弦值.
24.计算:
(1)﹣tan45°
(2)sin30°﹣cos245°+cot260°+sin260°
25.如图,在Rt△ABC中,∠B=90°,AB=10,sinA=,求BC的长.
26.小明家的脚踏式垃圾桶如图,当脚踩踏板时垃圾桶盖打开最大张角∠ABC=45°,为节省家里空间小明 想把垃圾桶放到桌下,经测量桌子下沿离地面高 55cm,垃圾桶高 BD=33.1cm,桶盖直径 BC=28.2cm,问垃圾桶放到桌下踩踏板时,桶盖完全打开有没有碰到桌子下沿?(≈1.41 )
参考答案
1. C 2. B 3.D 4.D 5.D 6. D 7.B 8. A 9. B 10. B
11..
12..
13..
14.
15.60°、.
16.
17.
18. 3 2
19.30°.
20.120.
21.(40+40)海里.
22.解:过点C作CG∥DA交AB于点G.
∵MN∥PQ,CG∥DA,
∴四边形AGCD是平行四边形.
∴AG=CD=50m,∠CGB=38°.
∴GB=AB﹣AG=120﹣50=70(m).
∴tan38°==0.78,
在Rt△BFC中,
tan70°==2.75,
∴BF=,
∴==0.78,
解得:CF≈76.2(m).
答:河流的宽是76.2米.
23.解:作PC⊥x轴于C.
∵tanα=,OC=3,
∴PC=4,即y=4.
则OP=5.
则sinα=.
24.解:(1)原式=﹣1=﹣1,
(2)原式=++=.
25.解:如图,∵在Rt△ABC中,∠B=90°,AB=10,sinA=,
∴=,
则AC=BC.
又由勾股定理得到:AB2+BC2=AC2,即102+BC2=BC2,
∴BC=7.5.
26解:过点C作CG⊥DE交AB于H.
由题意得:四边形ABDE是矩形,
∴AB∥DE,
∴∠CHB=90°,CH=BD=33.1,
在Rt△CBH中,sin∠CBH=,
∴CH=BC sin∠CBH=28.2×≈20,
∴CG=CH+HG=33.1+20=53.1<55,
答:桶盖完全打开时没有碰到碰到子下沿.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
