2021-2022学年 苏科版九年级数学下册 第七章 锐角三角函数 单元检测试题 (word版含答案)
文档属性
| 名称 | 2021-2022学年 苏科版九年级数学下册 第七章 锐角三角函数 单元检测试题 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 172.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 00:00:00 | ||
图片预览



文档简介
第七章 锐角三角函数 单元练习题
一、 选择题
1. 在中,,,,则的值为( )
A. B. C. D.
2. 在中,,若,则的值是
A. B. C. D.
3. 若,则的正切值的范围是( )
A. B. C. D.
4. 中,,若,则的长为( )
A. B. C. D.
5. 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
6. 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
A. B. C. D.
7. 身高相等的三名同学甲,乙,丙参加风筝比赛,三人放出风筝的线长,线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
同 学 甲 乙 丙
放出风筝线长 100 m 100 m 90 m
线与地面交角 40° 45° 60°
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
8. 某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价元,则购买这种草皮至少需要( )
A.元 B.元 C.元 D.
9. 如图,已知中,,,,,则的度数为( )
A. B. C. D.
10. 如图,两建筑物的水平距离为米,从点测得点的俯角为,测得点的俯角为,则较低建筑物的高为( )
A.米 B.米 C.米 D.米
二、 填空题
11. 已知三角形的两条边长分别是和,一个内角为,那么满足这一条件且彼此不全等的三角形共有________个.
12.某人在20米高的塔顶测得地面上的一点的俯角是60°,这点到塔底部的距离约为 (精确到0.1米).
13.山坡与地平面成30°的倾斜角,某人上坡走60米,则他上升的最大高度为 米,山坡的坡度是 .
14.将sin20°、cos20°、cos40°、cos80°的值由小到大的顺序排列 .
15. 某人沿着有一定坡度的坡面前进了米,此时他与水平地面的垂直距离为米,则这个坡面的坡度比为________.
16.在平面直角坐标系中,点A的坐标为(m,n),其中m≠0,点B的坐标为(0,5),若AB=3,记||=a,则a的取值范围为 .
17.如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB= m(用计算器计算,结果精确到0.1米)
18.一个小球由地面沿着坡度1:2的坡面向上前进了10米,此时小球距离地面的高度为 米.
19.已知一个斜坡的坡度i=1:,那么该斜坡的坡角的度数是 度.
20. 在中,已知,,则________.
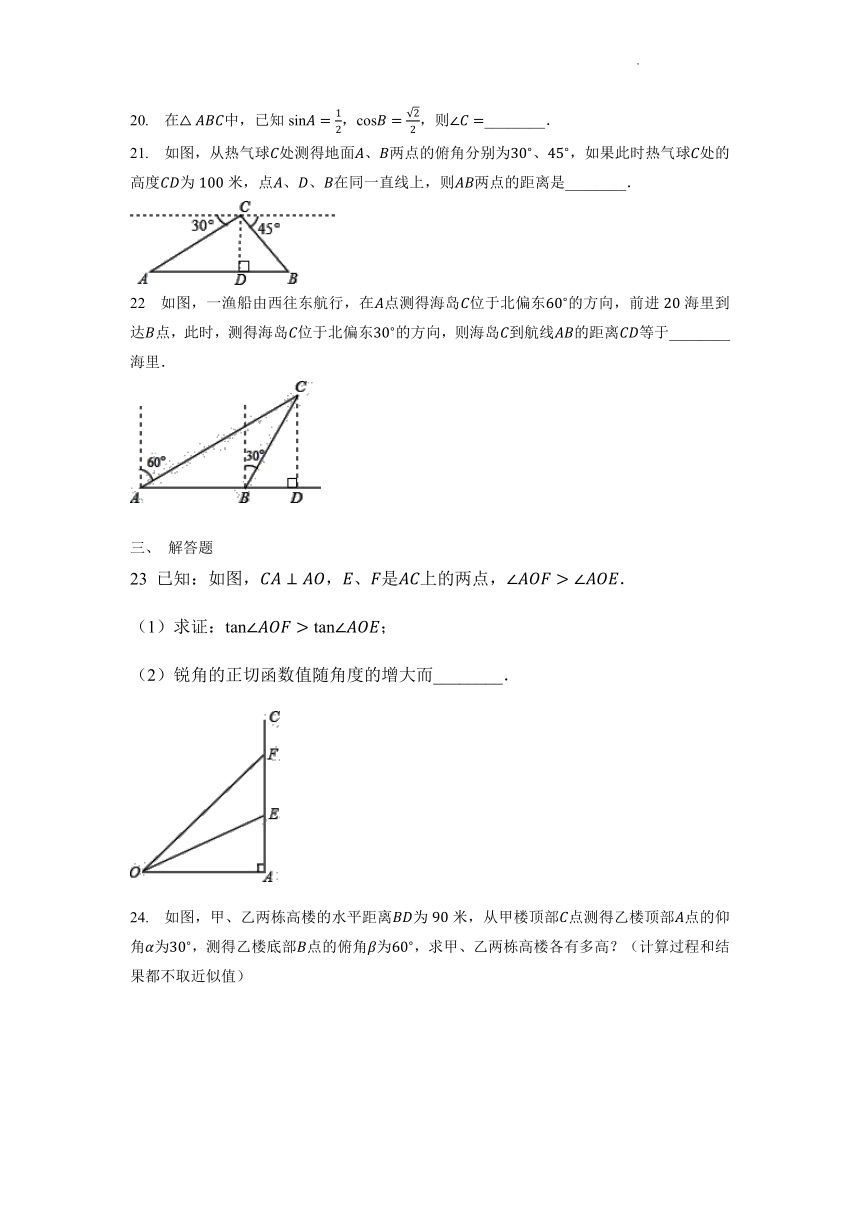
21. 如图,从热气球处测得地面、两点的俯角分别为、,如果此时热气球处的高度为米,点、、在同一直线上,则两点的距离是________.
22 如图,一渔船由西往东航行,在点测得海岛位于北偏东的方向,前进海里到达点,此时,测得海岛位于北偏东的方向,则海岛到航线的距离等于________海里.
三、 解答题
23 已知:如图,,、是上的两点,.
(1)求证:;
(2)锐角的正切函数值随角度的增大而________.
24. 如图,甲、乙两栋高楼的水平距离为米,从甲楼顶部点测得乙楼顶部点的仰角为,测得乙楼底部点的俯角为,求甲、乙两栋高楼各有多高?(计算过程和结果都不取近似值)
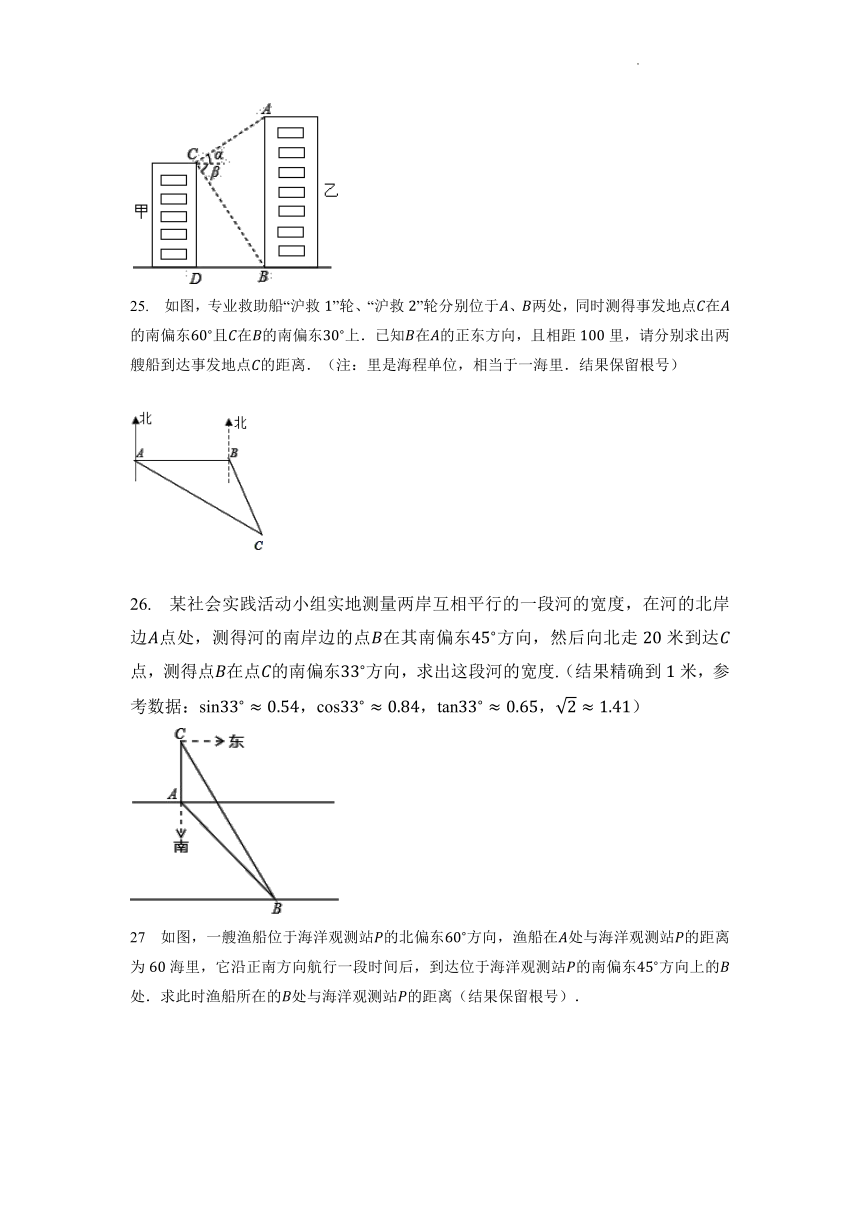
25. 如图,专业救助船“沪救”轮、“沪救”轮分别位于、两处,同时测得事发地点在的南偏东且在的南偏东上.已知在的正东方向,且相距里,请分别求出两艘船到达事发地点的距离.(注:里是海程单位,相当于一海里.结果保留根号)
26. 某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点处,测得河的南岸边的点在其南偏东方向,然后向北走米到达点,测得点在点的南偏东方向,求出这段河的宽度.(结果精确到米,参考数据:,,,)
27 如图,一艘渔船位于海洋观测站的北偏东方向,渔船在处与海洋观测站的距离为海里,它沿正南方向航行一段时间后,到达位于海洋观测站的南偏东方向上的处.求此时渔船所在的处与海洋观测站的距离(结果保留根号).
参考答案与试题解析
1. C 2. B 3.D 4. B 5.C 6. C 7.B 8. B 9. C 10. A
11.
12.11.5(米).
13.1:.
14.∴cos80°<sin20°<cos40°<cos20°.
15.
16.a≥.
17.11.9.
18.2米.
19.
20.米
21.
22.解:(1)∵AB=AC,∠B=36°,
∴∠C=∠B=36°,
∴∠BAC=180°﹣∠B﹣∠C=108°,
∵AB=BD,∠B=36°,
∴∠BAD=∠BDA=(180°﹣∠B)=72°,
∴∠CAD=∠BAC﹣∠BAD=108°﹣72°=36°,
即∠DAC=∠B,
∵∠C=∠C,
∴△CAD∽△CBA,
∴=,
∵AB=AC=BD=2,
∴=,
解得:CD=﹣1(负数舍去);
(2)
延长CB到E,使BE=AB=2,连接AE,
则∠E=∠BAE,
∵∠ABC=36°=∠E+∠BAE,
∴∠E=∠BAE=18°,
∵∠BAD=72°,
∴∠EAD=72°+18°=90°,
∵∠C=∠CAD=36°,
∴AD=CD=﹣1,
在Rt△EAD中,sinE===,
即sin18°=.
23.高楼的高度为,小玲在山坡上走过的距离为.
24.
【答案】
甲楼高为米,乙楼高为米.
【解答】
解:作于点.
∵ ,,且,
∴ 四边形是矩形.
∴ ,.
在中,,米.
∵ ,
∴ (米).
∴ (米).
在中,,米.
∵ ,
∴ (米).
∴ (米).
25.
【答案】
船到达事发地点的距离是里,船到达事发地点的距离是里.
【解答】
解:作于,
∵ 点在的南偏东,
∴ ,
∵ 在的南偏东,
∴ ,
∴ ,
∴ 里,
∴ 里,
里,
∴ 里.
26.
【答案】
解:如图,记河南岸为,延长交于点,则.
由题意知,,,
设米,则米,米,
在中,,
∴ ,
解得.
答:这段河宽约为.
【解答】
解:如图,记河南岸为,延长交于点,则.
由题意知,,,
设米,则米,米,
在中,,
∴ ,
解得.
答:这段河宽约为.
27【答案】
当渔船位于南偏东方向时,渔船与的距离是海里.
【解答】
解:过点作,垂足为,
根据题意可得出:,,,
在中,∵ ,
∴ ,
在中,∵ ,
∴ .
一、 选择题
1. 在中,,,,则的值为( )
A. B. C. D.
2. 在中,,若,则的值是
A. B. C. D.
3. 若,则的正切值的范围是( )
A. B. C. D.
4. 中,,若,则的长为( )
A. B. C. D.
5. 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A. B. C. D.
6. 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
A. B. C. D.
7. 身高相等的三名同学甲,乙,丙参加风筝比赛,三人放出风筝的线长,线与地面夹角如下表(假设风筝线是拉直的),则三人所放的风筝中( )
同 学 甲 乙 丙
放出风筝线长 100 m 100 m 90 m
线与地面交角 40° 45° 60°
A.甲的最高 B.丙的最高 C.乙的最低 D.丙的最低
8. 某市“旧城改造”中,计划在市内一块如图所示的三角形空地上种植某种草皮,以美化环境.已知这种草皮每平方米售价元,则购买这种草皮至少需要( )
A.元 B.元 C.元 D.
9. 如图,已知中,,,,,则的度数为( )
A. B. C. D.
10. 如图,两建筑物的水平距离为米,从点测得点的俯角为,测得点的俯角为,则较低建筑物的高为( )
A.米 B.米 C.米 D.米
二、 填空题
11. 已知三角形的两条边长分别是和,一个内角为,那么满足这一条件且彼此不全等的三角形共有________个.
12.某人在20米高的塔顶测得地面上的一点的俯角是60°,这点到塔底部的距离约为 (精确到0.1米).
13.山坡与地平面成30°的倾斜角,某人上坡走60米,则他上升的最大高度为 米,山坡的坡度是 .
14.将sin20°、cos20°、cos40°、cos80°的值由小到大的顺序排列 .
15. 某人沿着有一定坡度的坡面前进了米,此时他与水平地面的垂直距离为米,则这个坡面的坡度比为________.
16.在平面直角坐标系中,点A的坐标为(m,n),其中m≠0,点B的坐标为(0,5),若AB=3,记||=a,则a的取值范围为 .
17.如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB= m(用计算器计算,结果精确到0.1米)
18.一个小球由地面沿着坡度1:2的坡面向上前进了10米,此时小球距离地面的高度为 米.
19.已知一个斜坡的坡度i=1:,那么该斜坡的坡角的度数是 度.
20. 在中,已知,,则________.
21. 如图,从热气球处测得地面、两点的俯角分别为、,如果此时热气球处的高度为米,点、、在同一直线上,则两点的距离是________.
22 如图,一渔船由西往东航行,在点测得海岛位于北偏东的方向,前进海里到达点,此时,测得海岛位于北偏东的方向,则海岛到航线的距离等于________海里.
三、 解答题
23 已知:如图,,、是上的两点,.
(1)求证:;
(2)锐角的正切函数值随角度的增大而________.
24. 如图,甲、乙两栋高楼的水平距离为米,从甲楼顶部点测得乙楼顶部点的仰角为,测得乙楼底部点的俯角为,求甲、乙两栋高楼各有多高?(计算过程和结果都不取近似值)
25. 如图,专业救助船“沪救”轮、“沪救”轮分别位于、两处,同时测得事发地点在的南偏东且在的南偏东上.已知在的正东方向,且相距里,请分别求出两艘船到达事发地点的距离.(注:里是海程单位,相当于一海里.结果保留根号)
26. 某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点处,测得河的南岸边的点在其南偏东方向,然后向北走米到达点,测得点在点的南偏东方向,求出这段河的宽度.(结果精确到米,参考数据:,,,)
27 如图,一艘渔船位于海洋观测站的北偏东方向,渔船在处与海洋观测站的距离为海里,它沿正南方向航行一段时间后,到达位于海洋观测站的南偏东方向上的处.求此时渔船所在的处与海洋观测站的距离(结果保留根号).
参考答案与试题解析
1. C 2. B 3.D 4. B 5.C 6. C 7.B 8. B 9. C 10. A
11.
12.11.5(米).
13.1:.
14.∴cos80°<sin20°<cos40°<cos20°.
15.
16.a≥.
17.11.9.
18.2米.
19.
20.米
21.
22.解:(1)∵AB=AC,∠B=36°,
∴∠C=∠B=36°,
∴∠BAC=180°﹣∠B﹣∠C=108°,
∵AB=BD,∠B=36°,
∴∠BAD=∠BDA=(180°﹣∠B)=72°,
∴∠CAD=∠BAC﹣∠BAD=108°﹣72°=36°,
即∠DAC=∠B,
∵∠C=∠C,
∴△CAD∽△CBA,
∴=,
∵AB=AC=BD=2,
∴=,
解得:CD=﹣1(负数舍去);
(2)
延长CB到E,使BE=AB=2,连接AE,
则∠E=∠BAE,
∵∠ABC=36°=∠E+∠BAE,
∴∠E=∠BAE=18°,
∵∠BAD=72°,
∴∠EAD=72°+18°=90°,
∵∠C=∠CAD=36°,
∴AD=CD=﹣1,
在Rt△EAD中,sinE===,
即sin18°=.
23.高楼的高度为,小玲在山坡上走过的距离为.
24.
【答案】
甲楼高为米,乙楼高为米.
【解答】
解:作于点.
∵ ,,且,
∴ 四边形是矩形.
∴ ,.
在中,,米.
∵ ,
∴ (米).
∴ (米).
在中,,米.
∵ ,
∴ (米).
∴ (米).
25.
【答案】
船到达事发地点的距离是里,船到达事发地点的距离是里.
【解答】
解:作于,
∵ 点在的南偏东,
∴ ,
∵ 在的南偏东,
∴ ,
∴ ,
∴ 里,
∴ 里,
里,
∴ 里.
26.
【答案】
解:如图,记河南岸为,延长交于点,则.
由题意知,,,
设米,则米,米,
在中,,
∴ ,
解得.
答:这段河宽约为.
【解答】
解:如图,记河南岸为,延长交于点,则.
由题意知,,,
设米,则米,米,
在中,,
∴ ,
解得.
答:这段河宽约为.
27【答案】
当渔船位于南偏东方向时,渔船与的距离是海里.
【解答】
解:过点作,垂足为,
根据题意可得出:,,,
在中,∵ ,
∴ ,
在中,∵ ,
∴ .
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
