【课件】5.1 导数的概念及其意义 数学-RJ·A-选择性必修第二册(67页PPT)
文档属性
| 名称 | 【课件】5.1 导数的概念及其意义 数学-RJ·A-选择性必修第二册(67页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 16:25:18 | ||
图片预览










文档简介
(共67张PPT)
数学-RJ·A-选择性必修第二册
5.1 导数的概念及其意义
第五章 一元函数的导数及其应用
学习目标
1.通过实例分析,经历由平均变化率过渡到瞬时变化率的过程.
2.理解函数平均变化率、瞬时变化率的概念以及它们之间的关系.
3.掌握函数平均变化率、瞬时变化率的求法.
4.掌握导数的概念及其几何意义,会用导数的概念求简单函数在某点处的导数及曲线的切线问题.
重点:平均变化率、瞬时变化率的概念及求法、导数的概念及利用导数概念求导数、导数的几何意义及其应用
难点:平均变化率、瞬时变化率的概念以及两者之间关系的理解、导数概念的理解、导数几何意义的理解
知识梳理
一、变化率问题
问题1 高台跳水运动员的速度
探究:在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
h(t)=-4.9t2+4.8t+11.
如何描述运动员从起跳到入水的过程中运动的快慢程度呢?
提示:在上升阶段运动得越来越慢,在下降阶段运动得越来越快.
我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度近似地描述他的运动状态.
例如,在0≤t≤0.5这段时间里,= =2.35(m/s);
在1≤t≤2这段时间里,= =-9.9(m/s).
一般地,在t1≤t≤t2这段时间里,= =-4.9(t1+t2)+4.8.
思考:计算运动员在0≤t≤这段时间里的平均速度,你发现了什么?你认为用平均速度描述运动员的运动状态有什么问题吗?
提示(m/s).
用平均速度不能准确反映运动员在这一时间段里的运动状态.
瞬时速度的概念:
我们把物体在某一时刻的速度称为瞬时速度.
探究:瞬时速度与平均速度有什么关系?你能利用这种关系求运动员在t=1 s时的瞬时速度吗?
我们在t=1之后或之前,任意取一个时刻1+Δt.
Δt是时间改变量,可以是正值,也可以是负值,但不为0.
当Δt>0时,把运动员在时间段[1,1+Δt]内近似看成做匀速直线运动,计算时间段[1,1+Δt]内的平均速度,
用平均速度近似表示运动员在t=1时的瞬时速度.
当Δt<0时,在时间段[1+Δt,1]内可作类似处理.
提示:设运动员在t0时刻附近某一时间段内的平均速度是,如果不断缩短这一时间段的长度,那么将越来越趋近于运动员在t0时刻的瞬时速度.
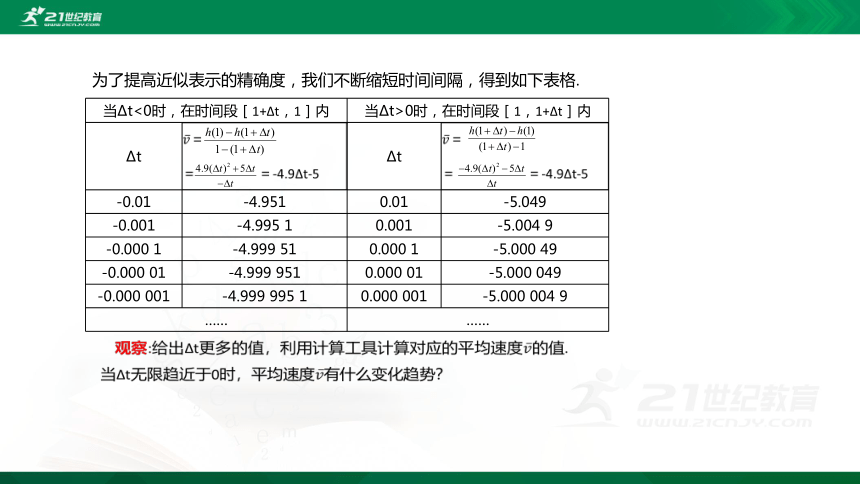
为了提高近似表示的精确度,我们不断缩短时间间隔,得到如下表格.
当Δt<0时,在时间段[1+Δt,1]内 当Δt>0时,在时间段[1,1+Δt]内
Δt = = =-4.9Δt-5 Δt =
= =-4.9Δt-5
-0.01 -4.951 0.01 -5.049
-0.001 -4.995 1 0.001 -5.004 9
-0.000 1 -4.999 51 0.000 1 -5.000 49
-0.000 01 -4.999 951 0.000 01 -5.000 049
-0.000 001 -4.999 995 1 0.000 001 -5.000 004 9
…… ……
观察:给出Δt更多的值,利用计算工具计算对应的平均速度的值.当Δt无限趋近于0时,平均速度有什么变化趋势?
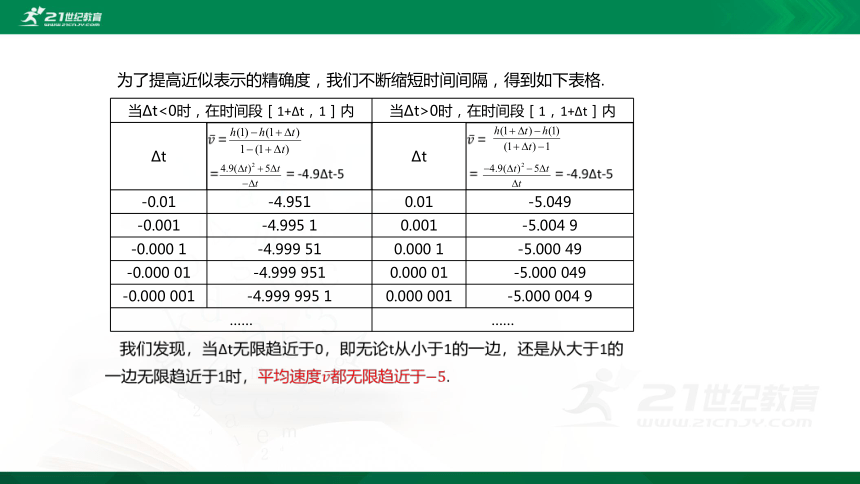
为了提高近似表示的精确度,我们不断缩短时间间隔,得到如下表格.
当Δt<0时,在时间段[1+Δt,1]内 当Δt>0时,在时间段[1,1+Δt]内
Δt = = =-4.9Δt-5 Δt =
= =-4.9Δt-5
-0.01 -4.951 0.01 -5.049
-0.001 -4.995 1 0.001 -5.004 9
-0.000 1 -4.999 51 0.000 1 -5.000 49
-0.000 01 -4.999 951 0.000 01 -5.000 049
-0.000 001 -4.999 995 1 0.000 001 -5.000 004 9
…… ……
我们发现,当Δt无限趋近于0,即无论t从小于1的一边,还是从大于1的一边无限趋近于1时,平均速度都无限趋近于.
事实上,由= =4.9Δt可以发现,当Δt无限趋近于0时,Δt也无限趋近于0,所以无限趋近于.这与前面得到的结论一致.
数学中,我们把叫做“当Δt无限趋近于0时,= 的极限”,
记为 .
从物理的角度看,当时间间隔|Δt|无限趋近于0时,平均速度就无限趋近于t=1时的瞬时速度.
因此,运动员在t=1 s时的瞬时速度v(1)= m/s.
思考: (1)求运动员在t=2 s时的瞬时速度;
(2)如何求运动员从起跳到入水过程中在某一时刻t0的瞬时速度?
问题2 抛物线的切线的斜率
探究:你认为应该如何定义抛物线在点处的切线?
提示:我们通常在点的附近任取一点,考察抛物线的割线的变化情况.
观察: 如图,当点P(x,x2)沿着抛物线f(x)=x2趋近于点P0(1,1)时,割线P0P有什么变化趋势?
提示:我们发现,当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置,
这个确定位置的直线P0T称为抛物线f(x)=x2在点P0(1,1)处的切线.
探究:我们知道,斜率是确定直线的一个要素.如何求抛物线f(x)=x2在点P0(1,1)处的切线P0T的斜率k0呢?
提示:从上述切线的定义可见,抛物线f(x)=x2在点P0(1,1)处的切线P0T的斜率与割线P0P的斜率有内在联系.
割线的斜率:记Δx=x-1,{1}则点P的坐标是(1+Δx,(1+Δx)2).
于是,割线P0P的斜率
我们可以用割线P0P的斜率k近似地表示切线P0T的斜率k0,并且可以通过不断缩短横坐标间隔|Δx|来提高近似表示的精确度,得到如下表格
Δx<0 Δx>0
Δx k=Δx+2 Δx k=Δx+2
-0.01 1.99 0.01 2.01
-0.001 1.999 0.001 2.001
-0.000 1 1.999 9 0.000 1 2.000 1
-0.000 01 1.999 99 0.000 01 2.000 01
-0.000 001 1.999 999 0.000 001 2.000 001
…… ……
观察:利用计算工具计算更多割线P0P的斜率k的值,当Δx无限趋近于0时,割线P0P的斜率k有什么变化趋势?
Δx<0 Δx>0
Δx k=Δx+2 Δx k=Δx+2
-0.01 1.99 0.01 2.01
-0.001 1.999 0.001 2.001
-0.000 1 1.999 9 0.000 1 2.000 1
-0.000 01 1.999 99 0.000 01 2.000 01
-0.000 001 1.999 999 0.000 001 2.000 001
…… ……
割线P0P的斜率k都无限趋近于2.
事实上,由可以直接看出,当无限趋近于0时, +2无限趋近于2.
我们把2叫做“当无限趋近于0时,的极限”,
记为
从几何图形上看,当横坐标间隔|Δx|无限变小时,点P无限趋近于点P0,于是割线P0P无限趋近于点P0处的切线P0T.这时,割线P0P的斜率k无限趋近于点P0处的切线P0T的斜率k0.因此,切线P0T的斜率k0=2.
思考:你认为应该怎样定义抛物线f(x)=x2在点(x0,x02)处的切线?试求抛物线f(x)=x2在点(-1,1)处切线的斜率.
提示:在点P0(x0,x02)的附近任取一点P(x,x2),当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置P0T,这个确定位置P0T称为抛物线f(x)=x2在点(x0,x02)处的切线.
抛物线f(x)=x2在点(-1,1)处的切线的斜率为
平均变化率的概念:
对于函数y=f(x),设自变量x从x0变化到x0+Δx,相应地,函数值y就从f(x0)变化到f(x0+Δx).这时,x的变化量为Δx,y的变化量为.
我们把比值,即叫做函数y=f(x)从x0到x0+Δx的平均变化率.
(1)一般地,在式子==中,当x1取定值,Δx取不同数值时,函数的平均变化率不一定相同;当Δx取定值,x1取不同数值时,函数的平均变化率也不一定相同.特别地,当函数f(x)为常数函数时,Δy=0,则=0.
(2)平均变化率=的几何意义就是函数y=f(x)图象上的两点(x0,f(x0))与(x0+Δx,f(x0+Δx))所在直线的斜率.
(3)利用平均变化率可以刻画变量平均变化的趋势和快慢程度,但效果是“粗糙、不精确的”.只有当Δx=x2-x1无限趋近于0时,这种量化才由“粗糙”趋近“精确”.
理解平均变化率要注意以下三点:
二、导数的概念
如果当Δx→0时,平均变化率无限趋近于一个确定的值,即有极限,则称y=f(x)在x=x0处可导,并把这个确定的值叫做y=f(x)在x=x0处的导数(derivative)(也称为瞬时变化率),记作f ′(x0)或,即
由导数的定义可知,
问题1中运动员在t=1时的瞬时速度v(1),就是函数h(t)=
-4.9t2+4.8t+11在t=1处的导数h ′(1);
问题2中抛物线f(x)=x2在点P0(1,1)处的切线P0T的斜率k0,就是函数f(x)=x2在x=1处的导数f ′(1).
实际上,导数可以描述任何运动变化事物的瞬时变化率,如效率、国内生产总值(GDP)的增长率等.
对于y=f(x)在x=x0处的导数的理解要注意以下三点:
(1)y=f(x)在x=x0处的导数即为函数y=f(x)在x=x0处的瞬时变化率,导数可以描述任何事物的瞬时变化率,应用非常广泛.
(2)y=f(x)在x=x0处的导数表示为f ′(x0)或,函数在x=x0处的导数f ′(x0)只与x0有关,与Δx无关.函数在某点处的导数是一个定值,是函数在该点的函数值的改变量与自变量的改变量比值的极限,不是变量.
(3)若极限 不存在,则称函数y=f(x)在x=x0处不可导.
三、导数的几何意义
思考:观察函数y=f(x)的图象,平均变化率 表示什么?瞬时变化率 表示什么?
平均变化率 表示割线P0P的斜率.
如图,在曲线上任取一点如果当点沿着曲线无限趋近于点时,割线无限趋近于一个确定的位置,这个确定位置的直线P0T称为曲线在点P0处的切线.
与问题2中抛物线的割线和切线之间的关系类似,容易知道,割线P0P的斜率k=.
记Δx=x-x0,当点P沿着曲线y=f(x)无限趋近于点P0时,即当Δx→0时,k无限趋近于函数y=f(x)在x=x0处的导数.因此,函数y=f(x)在x=x0处的导数f ′(x0)就是切线P0T的斜率k0,即
这就是导数的几何意义.
继续观察上图,可以发现点P0处的切线P0T比任何一条割线更贴近点P0附近的曲线.
进一步地,利用信息技术工具将点P0附近的曲线不断放大(如图),可以发现点P0附近的曲线越来越接近于直线.因此,在点P0附近,曲线y=f(x)可以用点P0处的切线P0T近似代替.
理解导数的几何意义应注意以下三点:
(1)函数y=f(x)在x=x0处的导数即为曲线 y=f(x)在点(x0,f(x0))处的切线的斜率,即曲线y=f(x)在点(x0,f(x0)处的切线的斜率k=f ′(x0).此时曲线y=f(x)在点(x0,f(x0))处的切线方程为y-f(x0)=f ′(x0)(x-x0).如果切线的倾斜角为α,则tan α=f ′(x0).
(2)若函数y=f(x)在点P(x0,f(x0))处的导数不存在,表明曲线在该点处有切线,且切线与x轴垂直或曲线在该点处无切线.
(3)利用以直代曲以及导数的几何意义可知:当曲线y=f(x)在点(x0,f(x0))处的切线的斜率f ′(x0)>0时,函数y=f(x)在x0附近单调递增;当曲线y=f(x)在点(x0,f(x0))处的切线的斜率f ′(x0)<0时,函数y=f(x)在x0附近单调递减;当曲线y=f(x)在点(x0,f(x0))处的切线的斜率f ′(x0)=0时,函数y=f(x0)在x0附近不增不减.
四、导函数的概念
从求函数在处导数的过程可以看到,当时,是一个唯一确定的数.这样,当x变化时,就是x的函数,我们称它为的导函数(derived function)(简称导数).y=f(x)的导函数有时也记作y′,即
函数f(x)在x=x0处的导数f ′(x0)、导函数f ′(x)之间的区别与联系:
(1)区别:①f ′(x0)是在x=x0处函数值的改变量与自变量的改变量之比的极限,是一个常数,不是变量.
② f ′(x)是函数f(x)的导函数,是对某一区间内任意x而言的.
(2)联系:函数f(x)在x=x0处的导数f ′(x0)就是导函数f ′(x)在x=x0处的函数值.
常考题型
一、求平均速度与瞬时速度
例1 若一物体运动方程如下(位移s的单位:m,时间t的单位:s):
求:(1)物体在t∈[3,5]内的平均速度;
(2)物体的初速度v0;
(3)物体在t=1时的瞬时速度.
【解】(1)∵ 当t∈[3,5]时,时间变化量Δt=5-3=2,
位移变化量Δs=3×52+2-(3×32+2)=3×(52-32)=48,
∴ 物体在t∈[3,5]内的平均速度为==24(m/s).
(2)求物体的初速度v0,即求物体在t=0时的瞬时速度.
∵ 物体在t=0附近的平均速度为
∴ 物体在t=0时的瞬时速度为 (m/s).
(3)物体在t=1时的瞬时速度即为函数在t=1处的瞬时变化率.
∵ 函数在t=1处的平均变化率为
∴ 物体在t=1时的瞬时速度为 (m/s).
◆求瞬时速度的三个步骤
1.求位移变化量,给出时间的一个变化量Δt,求相应位移的变化量Δs.
2.求平均速度,.
3.求极限,得瞬时速度,即
训练题
1.(1)已知某质点的运动方程为s(t)=t2+3,则t从3到3.3,该质点运动的平均速度为 ( )
A.6.3 B.36.3 C.3.3 D.9.3
(2)甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图所示,则从0到t0这段时间内甲、乙两人的平均速度较大的是 (填甲或乙).
2.[2020·吉林省实验中学高二期末]已知某物体的运动方程是s=+t,则当t=3时,该物体的瞬时速度是 ( )
A.2 B.3 C.4 D.5
A
乙
C
3.已知物体的运动方程为s=v0t+at2,试求该物体在t=1时的瞬时速度.
解:∵ Δs=v0(1+Δt)+a(1+Δt)2-
=v0Δt+aΔt+a(Δt)2,
∴=v0+a+aΔt,
∴ 该物体在t=1时的瞬时速度为
二、求函数的平均变化率、导数(瞬时变化率)
1.求函数在某一区间的平均变化率
例2 求函数y=f(x)=在区间[1,1+Δx]内的平均变化率.
◆求函数的平均变化率的三个步骤
1.作差求自变量的变化量Δx=x2-x1;
2.作差求函数值的变化量Δy=f(x2)-f(x1);
3.作商求平均变化率
训练题
1.[2020·安徽高二期末]在曲线y=x2上取一点(1,1)及附近一点(1+Δx,1+Δy),则为 ( )
A.Δx++2 B.Δx--2 C.Δx+2 D.2+Δx-
2.[2020·山西应县一中高二期末]在x=1附近,取Δx=0.3,在四个函数①f(x)=x;②f(x)=x2;③f(x)=x3;④f(x)=中,平均变化率最大的是 (填序号).
3.[2020·山东临沂一中月考]已知函数f (x)=ax2在区间 [1,2]上的平均变化率为,则f(x)在区间[-2,-1]上的平均变化率为 .
C
③
2.求函数在某一点处的导数
例3 求f (x)=x3-x在x=2处的导数.
【解】∵ Δy=f(2+Δx)-f(2)=(2+Δx)3-(2+Δx)-(23-2)
=(Δx)3+6(Δx)2+11Δx,
∴=(Δx)2+6Δx+11,
即f ′(2)=11.
训练题 [2019·吉林长春外国语学校高二检测]函数f(x)=x2-3在x=1处的瞬时变化率为 ( )
A. (Δx)2+2Δx B.Δx+2 C.2 D.4
C
3.根据导数定义求参数
例4 已知f (x)=ax3+3x2+2,若f ′(-1)=4,则a的值为( )
A. B. C. D.
【解析】因为Δy=f(x+Δx)-f(x)
=a(x+Δx)3+3(x+Δx)2+2-(ax3+3x2+2)
=3ax2·Δx+3ax(Δx)2+a(Δx)3+6x·Δx+3(Δx)2,
所以=3ax2+3ax·Δx+a(Δx)2+6x+3Δx,
所以 =3ax2+6x,即f ′(x)=3ax2+6x,
所以f ′(-1)=3a-6=4,解得a=.
【答案】C
4.根据导数定义求极限值
例5 [2020·山东兰陵二中高二检测]已知函数f (x)在x0处的导数为f ′(x0),则 等于 ( )
A.mf ′(x0) B.mf ′(x0)
C.f ′(x0) D.f ′(x0)
【答案】B
◆根据导数定义求极限值的方法
1.将已知极限式配凑成定义式的形式;
2.根据导数的定义得极限式的值.
C
2a
B
三、平均变化率、导数(瞬时变化率)的几何意义
1.曲线的割线及其应用
例6 已知曲线y=x2-1上两点A(2,3),B(2+Δx,3+Δy),当Δx=1时,割线AB的斜率是 ;当Δx=0.1时,割线AB的斜率是 .
【答案】5 4.1
训练题 设a=,b=2-,c=-2,则a,b,c的大小顺序为 ( )
A.a>b>c B.b>c>a C.c>a>b D.a>c>b
A
2.利用导数的几何意义描述函数图象
例7 一堆雪在融化过程中,其体积V(单位:m3)与融化时间t(单位:h)近似满足函数关系:V(t)=(H为常数),其图象如图所示.记这堆雪从融化开始到结束的平均融化速度为(m3/h).那么t1,t2,t3,t4中,瞬时融化速度等于(m3/h)的时刻是 .
【解析】由题意,可得平均融化速度
反映的是V(t)的图象与坐标轴交点连线的斜率,
观察可知t3处瞬时融化速度与平均融化速度一致.
【答案】t3
◆导数的几何意义
函数y=f(x)在x0处的导数f ′(x0)的几何意义,就是曲线y=f(x)在
点(x0,f(x0))处切线的斜率k,即k=f ′(x0)=
训练题
1.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f ′(x)的图象可能为 ( )
D
A B C D
2.[2020·安徽合肥高二期末]函数y=f(x)的图象如图所示,
f ′(x)是函数f(x)的导函数,下列数值排序正确的是 ( )
A.f ′(2)B.f ′(3)C.f(3)-f(2)D.f ′(2)3. f ′(x)是函数y=f(x)的导函数,若y=f ′(x)的图象
如图所示,则函数y=f(x)的图象可能是 ( )
A B C D
D
D
◆判断导函数的图象和函数图象的关系的方法
1.正则升,负则降.导数值为正时,函数图象呈上升趋势;导数值为负时,函数图象呈下降趋势.
2.大则陡,小则缓.导数的绝对值越大,函数图象越陡峭;导数的绝对值越小,函数图象越平缓.
3.求曲线的切线方程
例8 [2020·江西南昌二中高二期末]已知函数f(x)=x3+x-2.
(1)求曲线y=f(x)在点(2,8)处的切线方程;
(2)直线为曲线y=f(x)的切线,且经过原点,求直线的方程及切点坐标.
【解】
(1)因为f ′(2)=13,
所以曲线y=f(x)在点(2,8)处的切线方程为y-8=13(x-2),即13x-y-18=0.
(2)设切点为(x0, +x0-2),则f ′(x0)=3+1,
所以切线方程为y-(+x0-2)=(3+1)(x-x0).
因为切线过原点,
所以-(+x0-2)=-x0(3+1).
所以2=-2,解得x0=-1.
所以切点坐标为(-1,-4).
因为f ′(-1)=4,所以所求切线方程为y=4x.
◆利用导数的几何意义求曲线的切线方程的步骤
1. 求曲线y=f(x)在点P(x0,f(x0))处的切线方程的步骤
(1)求出函数y=f(x)在x0处的导数f ′(x0);
(2)根据直线方程的点斜式,得切线方程为
y-f(x0)=f ′(x0)(x-x0).
2. 求曲线y=f(x)过点P(x0,y0)的切线方程的步骤
(1)设切点为P′(x′,f(x′)),求切线的斜率k=f ′(x′),
写出切线方程(含参);
(2)把点P(x0,y0)的坐标代入切线方程,建立关于x′的方程,
解得x′的值,进而求出切线方程.
训练题
1.[2020·山东兰陵一中高二期末]已知f (x)=2x2,则曲线y=f(x)在点P(1,2)处的切线的倾斜角的正切值为 .
2.已知直线ax-by-2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则的值为 ( )
A. B. C. D.
3.[2020·安徽合肥高二检测]如图所示,函数y=f(x)的图象在点P处的切线方程是,则=( )
A.1 B.2 C.3 D.4
D
4
A
4.已知曲线f(x)=.
(1)求曲线过点A(1,0)的切线方程;
(2)求曲线的斜率为的切线的方程.
5.已知直线l1为曲线y=x2+x-2在点(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2.
(1)求直线l2的方程;
(2)求由直线l1,l2和x轴所围成的三角形的面积.
4.已知函数图象上某点处的切线方程求参数
例9 已知直线l:y=4x+a和曲线C:y=f (x)=x3-2x2+3相切,求a的值及切点坐标.
◆已知函数图象上某点处的切线方程求参数的方法
解题的关键是得到关于参数的方程(组),常根据以下结论列方程(组):
1.利用切点在曲线上可得关于参数的方程;
2.利用函数y=f(x)在x=x0处的导数即为曲线y=f(x)在点(x0,f(x0))处切线的斜率可得参数方程;
3.利用切点坐标满足切线方程可得参数方程.
训练题 [2020·广东东莞高二期末]若曲线y=x2+ax+b在点(1,1)处的切线为3x-y-2=0,则有 ( )
A.a=-1,b=1 B.a=1,b=-1
C.a=-2,b=1 D.a=2,b=-1
B
5.利用切线求最值问题
例10 已知直线x+2y-4=0与抛物线y2=2x相交于A,B两点,O是坐标原点,试在抛物线的曲线AOB上求一点P,使△ABP的面积最大.
◆利用切线求最值的一般思路
1.利用导数的几何意义可以解决一些与距离、面积相关的几何最值问题;
2.解决此类问题的关键是准确确定所求切线的位置,进而求出切点坐标;
3.曲线上点到直线的距离的最值问题常常转化为两平行线间的距离;
4.求切点可利用导数与待定系数法.
训练题 [2020·安徽芜湖高二期末]已知A,B,C三点在曲线y=上,其横坐标依次为1,m,4(1A.3 B. C. D.
B
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-选择性必修第二册
5.1 导数的概念及其意义
第五章 一元函数的导数及其应用
学习目标
1.通过实例分析,经历由平均变化率过渡到瞬时变化率的过程.
2.理解函数平均变化率、瞬时变化率的概念以及它们之间的关系.
3.掌握函数平均变化率、瞬时变化率的求法.
4.掌握导数的概念及其几何意义,会用导数的概念求简单函数在某点处的导数及曲线的切线问题.
重点:平均变化率、瞬时变化率的概念及求法、导数的概念及利用导数概念求导数、导数的几何意义及其应用
难点:平均变化率、瞬时变化率的概念以及两者之间关系的理解、导数概念的理解、导数几何意义的理解
知识梳理
一、变化率问题
问题1 高台跳水运动员的速度
探究:在一次高台跳水运动中,某运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系
h(t)=-4.9t2+4.8t+11.
如何描述运动员从起跳到入水的过程中运动的快慢程度呢?
提示:在上升阶段运动得越来越慢,在下降阶段运动得越来越快.
我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度近似地描述他的运动状态.
例如,在0≤t≤0.5这段时间里,= =2.35(m/s);
在1≤t≤2这段时间里,= =-9.9(m/s).
一般地,在t1≤t≤t2这段时间里,= =-4.9(t1+t2)+4.8.
思考:计算运动员在0≤t≤这段时间里的平均速度,你发现了什么?你认为用平均速度描述运动员的运动状态有什么问题吗?
提示(m/s).
用平均速度不能准确反映运动员在这一时间段里的运动状态.
瞬时速度的概念:
我们把物体在某一时刻的速度称为瞬时速度.
探究:瞬时速度与平均速度有什么关系?你能利用这种关系求运动员在t=1 s时的瞬时速度吗?
我们在t=1之后或之前,任意取一个时刻1+Δt.
Δt是时间改变量,可以是正值,也可以是负值,但不为0.
当Δt>0时,把运动员在时间段[1,1+Δt]内近似看成做匀速直线运动,计算时间段[1,1+Δt]内的平均速度,
用平均速度近似表示运动员在t=1时的瞬时速度.
当Δt<0时,在时间段[1+Δt,1]内可作类似处理.
提示:设运动员在t0时刻附近某一时间段内的平均速度是,如果不断缩短这一时间段的长度,那么将越来越趋近于运动员在t0时刻的瞬时速度.
为了提高近似表示的精确度,我们不断缩短时间间隔,得到如下表格.
当Δt<0时,在时间段[1+Δt,1]内 当Δt>0时,在时间段[1,1+Δt]内
Δt = = =-4.9Δt-5 Δt =
= =-4.9Δt-5
-0.01 -4.951 0.01 -5.049
-0.001 -4.995 1 0.001 -5.004 9
-0.000 1 -4.999 51 0.000 1 -5.000 49
-0.000 01 -4.999 951 0.000 01 -5.000 049
-0.000 001 -4.999 995 1 0.000 001 -5.000 004 9
…… ……
观察:给出Δt更多的值,利用计算工具计算对应的平均速度的值.当Δt无限趋近于0时,平均速度有什么变化趋势?
为了提高近似表示的精确度,我们不断缩短时间间隔,得到如下表格.
当Δt<0时,在时间段[1+Δt,1]内 当Δt>0时,在时间段[1,1+Δt]内
Δt = = =-4.9Δt-5 Δt =
= =-4.9Δt-5
-0.01 -4.951 0.01 -5.049
-0.001 -4.995 1 0.001 -5.004 9
-0.000 1 -4.999 51 0.000 1 -5.000 49
-0.000 01 -4.999 951 0.000 01 -5.000 049
-0.000 001 -4.999 995 1 0.000 001 -5.000 004 9
…… ……
我们发现,当Δt无限趋近于0,即无论t从小于1的一边,还是从大于1的一边无限趋近于1时,平均速度都无限趋近于.
事实上,由= =4.9Δt可以发现,当Δt无限趋近于0时,Δt也无限趋近于0,所以无限趋近于.这与前面得到的结论一致.
数学中,我们把叫做“当Δt无限趋近于0时,= 的极限”,
记为 .
从物理的角度看,当时间间隔|Δt|无限趋近于0时,平均速度就无限趋近于t=1时的瞬时速度.
因此,运动员在t=1 s时的瞬时速度v(1)= m/s.
思考: (1)求运动员在t=2 s时的瞬时速度;
(2)如何求运动员从起跳到入水过程中在某一时刻t0的瞬时速度?
问题2 抛物线的切线的斜率
探究:你认为应该如何定义抛物线在点处的切线?
提示:我们通常在点的附近任取一点,考察抛物线的割线的变化情况.
观察: 如图,当点P(x,x2)沿着抛物线f(x)=x2趋近于点P0(1,1)时,割线P0P有什么变化趋势?
提示:我们发现,当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置,
这个确定位置的直线P0T称为抛物线f(x)=x2在点P0(1,1)处的切线.
探究:我们知道,斜率是确定直线的一个要素.如何求抛物线f(x)=x2在点P0(1,1)处的切线P0T的斜率k0呢?
提示:从上述切线的定义可见,抛物线f(x)=x2在点P0(1,1)处的切线P0T的斜率与割线P0P的斜率有内在联系.
割线的斜率:记Δx=x-1,{1}则点P的坐标是(1+Δx,(1+Δx)2).
于是,割线P0P的斜率
我们可以用割线P0P的斜率k近似地表示切线P0T的斜率k0,并且可以通过不断缩短横坐标间隔|Δx|来提高近似表示的精确度,得到如下表格
Δx<0 Δx>0
Δx k=Δx+2 Δx k=Δx+2
-0.01 1.99 0.01 2.01
-0.001 1.999 0.001 2.001
-0.000 1 1.999 9 0.000 1 2.000 1
-0.000 01 1.999 99 0.000 01 2.000 01
-0.000 001 1.999 999 0.000 001 2.000 001
…… ……
观察:利用计算工具计算更多割线P0P的斜率k的值,当Δx无限趋近于0时,割线P0P的斜率k有什么变化趋势?
Δx<0 Δx>0
Δx k=Δx+2 Δx k=Δx+2
-0.01 1.99 0.01 2.01
-0.001 1.999 0.001 2.001
-0.000 1 1.999 9 0.000 1 2.000 1
-0.000 01 1.999 99 0.000 01 2.000 01
-0.000 001 1.999 999 0.000 001 2.000 001
…… ……
割线P0P的斜率k都无限趋近于2.
事实上,由可以直接看出,当无限趋近于0时, +2无限趋近于2.
我们把2叫做“当无限趋近于0时,的极限”,
记为
从几何图形上看,当横坐标间隔|Δx|无限变小时,点P无限趋近于点P0,于是割线P0P无限趋近于点P0处的切线P0T.这时,割线P0P的斜率k无限趋近于点P0处的切线P0T的斜率k0.因此,切线P0T的斜率k0=2.
思考:你认为应该怎样定义抛物线f(x)=x2在点(x0,x02)处的切线?试求抛物线f(x)=x2在点(-1,1)处切线的斜率.
提示:在点P0(x0,x02)的附近任取一点P(x,x2),当点P无限趋近于点P0时,割线P0P无限趋近于一个确定的位置P0T,这个确定位置P0T称为抛物线f(x)=x2在点(x0,x02)处的切线.
抛物线f(x)=x2在点(-1,1)处的切线的斜率为
平均变化率的概念:
对于函数y=f(x),设自变量x从x0变化到x0+Δx,相应地,函数值y就从f(x0)变化到f(x0+Δx).这时,x的变化量为Δx,y的变化量为.
我们把比值,即叫做函数y=f(x)从x0到x0+Δx的平均变化率.
(1)一般地,在式子==中,当x1取定值,Δx取不同数值时,函数的平均变化率不一定相同;当Δx取定值,x1取不同数值时,函数的平均变化率也不一定相同.特别地,当函数f(x)为常数函数时,Δy=0,则=0.
(2)平均变化率=的几何意义就是函数y=f(x)图象上的两点(x0,f(x0))与(x0+Δx,f(x0+Δx))所在直线的斜率.
(3)利用平均变化率可以刻画变量平均变化的趋势和快慢程度,但效果是“粗糙、不精确的”.只有当Δx=x2-x1无限趋近于0时,这种量化才由“粗糙”趋近“精确”.
理解平均变化率要注意以下三点:
二、导数的概念
如果当Δx→0时,平均变化率无限趋近于一个确定的值,即有极限,则称y=f(x)在x=x0处可导,并把这个确定的值叫做y=f(x)在x=x0处的导数(derivative)(也称为瞬时变化率),记作f ′(x0)或,即
由导数的定义可知,
问题1中运动员在t=1时的瞬时速度v(1),就是函数h(t)=
-4.9t2+4.8t+11在t=1处的导数h ′(1);
问题2中抛物线f(x)=x2在点P0(1,1)处的切线P0T的斜率k0,就是函数f(x)=x2在x=1处的导数f ′(1).
实际上,导数可以描述任何运动变化事物的瞬时变化率,如效率、国内生产总值(GDP)的增长率等.
对于y=f(x)在x=x0处的导数的理解要注意以下三点:
(1)y=f(x)在x=x0处的导数即为函数y=f(x)在x=x0处的瞬时变化率,导数可以描述任何事物的瞬时变化率,应用非常广泛.
(2)y=f(x)在x=x0处的导数表示为f ′(x0)或,函数在x=x0处的导数f ′(x0)只与x0有关,与Δx无关.函数在某点处的导数是一个定值,是函数在该点的函数值的改变量与自变量的改变量比值的极限,不是变量.
(3)若极限 不存在,则称函数y=f(x)在x=x0处不可导.
三、导数的几何意义
思考:观察函数y=f(x)的图象,平均变化率 表示什么?瞬时变化率 表示什么?
平均变化率 表示割线P0P的斜率.
如图,在曲线上任取一点如果当点沿着曲线无限趋近于点时,割线无限趋近于一个确定的位置,这个确定位置的直线P0T称为曲线在点P0处的切线.
与问题2中抛物线的割线和切线之间的关系类似,容易知道,割线P0P的斜率k=.
记Δx=x-x0,当点P沿着曲线y=f(x)无限趋近于点P0时,即当Δx→0时,k无限趋近于函数y=f(x)在x=x0处的导数.因此,函数y=f(x)在x=x0处的导数f ′(x0)就是切线P0T的斜率k0,即
这就是导数的几何意义.
继续观察上图,可以发现点P0处的切线P0T比任何一条割线更贴近点P0附近的曲线.
进一步地,利用信息技术工具将点P0附近的曲线不断放大(如图),可以发现点P0附近的曲线越来越接近于直线.因此,在点P0附近,曲线y=f(x)可以用点P0处的切线P0T近似代替.
理解导数的几何意义应注意以下三点:
(1)函数y=f(x)在x=x0处的导数即为曲线 y=f(x)在点(x0,f(x0))处的切线的斜率,即曲线y=f(x)在点(x0,f(x0)处的切线的斜率k=f ′(x0).此时曲线y=f(x)在点(x0,f(x0))处的切线方程为y-f(x0)=f ′(x0)(x-x0).如果切线的倾斜角为α,则tan α=f ′(x0).
(2)若函数y=f(x)在点P(x0,f(x0))处的导数不存在,表明曲线在该点处有切线,且切线与x轴垂直或曲线在该点处无切线.
(3)利用以直代曲以及导数的几何意义可知:当曲线y=f(x)在点(x0,f(x0))处的切线的斜率f ′(x0)>0时,函数y=f(x)在x0附近单调递增;当曲线y=f(x)在点(x0,f(x0))处的切线的斜率f ′(x0)<0时,函数y=f(x)在x0附近单调递减;当曲线y=f(x)在点(x0,f(x0))处的切线的斜率f ′(x0)=0时,函数y=f(x0)在x0附近不增不减.
四、导函数的概念
从求函数在处导数的过程可以看到,当时,是一个唯一确定的数.这样,当x变化时,就是x的函数,我们称它为的导函数(derived function)(简称导数).y=f(x)的导函数有时也记作y′,即
函数f(x)在x=x0处的导数f ′(x0)、导函数f ′(x)之间的区别与联系:
(1)区别:①f ′(x0)是在x=x0处函数值的改变量与自变量的改变量之比的极限,是一个常数,不是变量.
② f ′(x)是函数f(x)的导函数,是对某一区间内任意x而言的.
(2)联系:函数f(x)在x=x0处的导数f ′(x0)就是导函数f ′(x)在x=x0处的函数值.
常考题型
一、求平均速度与瞬时速度
例1 若一物体运动方程如下(位移s的单位:m,时间t的单位:s):
求:(1)物体在t∈[3,5]内的平均速度;
(2)物体的初速度v0;
(3)物体在t=1时的瞬时速度.
【解】(1)∵ 当t∈[3,5]时,时间变化量Δt=5-3=2,
位移变化量Δs=3×52+2-(3×32+2)=3×(52-32)=48,
∴ 物体在t∈[3,5]内的平均速度为==24(m/s).
(2)求物体的初速度v0,即求物体在t=0时的瞬时速度.
∵ 物体在t=0附近的平均速度为
∴ 物体在t=0时的瞬时速度为 (m/s).
(3)物体在t=1时的瞬时速度即为函数在t=1处的瞬时变化率.
∵ 函数在t=1处的平均变化率为
∴ 物体在t=1时的瞬时速度为 (m/s).
◆求瞬时速度的三个步骤
1.求位移变化量,给出时间的一个变化量Δt,求相应位移的变化量Δs.
2.求平均速度,.
3.求极限,得瞬时速度,即
训练题
1.(1)已知某质点的运动方程为s(t)=t2+3,则t从3到3.3,该质点运动的平均速度为 ( )
A.6.3 B.36.3 C.3.3 D.9.3
(2)甲、乙两人走过的路程s1(t),s2(t)与时间t的关系如图所示,则从0到t0这段时间内甲、乙两人的平均速度较大的是 (填甲或乙).
2.[2020·吉林省实验中学高二期末]已知某物体的运动方程是s=+t,则当t=3时,该物体的瞬时速度是 ( )
A.2 B.3 C.4 D.5
A
乙
C
3.已知物体的运动方程为s=v0t+at2,试求该物体在t=1时的瞬时速度.
解:∵ Δs=v0(1+Δt)+a(1+Δt)2-
=v0Δt+aΔt+a(Δt)2,
∴=v0+a+aΔt,
∴ 该物体在t=1时的瞬时速度为
二、求函数的平均变化率、导数(瞬时变化率)
1.求函数在某一区间的平均变化率
例2 求函数y=f(x)=在区间[1,1+Δx]内的平均变化率.
◆求函数的平均变化率的三个步骤
1.作差求自变量的变化量Δx=x2-x1;
2.作差求函数值的变化量Δy=f(x2)-f(x1);
3.作商求平均变化率
训练题
1.[2020·安徽高二期末]在曲线y=x2上取一点(1,1)及附近一点(1+Δx,1+Δy),则为 ( )
A.Δx++2 B.Δx--2 C.Δx+2 D.2+Δx-
2.[2020·山西应县一中高二期末]在x=1附近,取Δx=0.3,在四个函数①f(x)=x;②f(x)=x2;③f(x)=x3;④f(x)=中,平均变化率最大的是 (填序号).
3.[2020·山东临沂一中月考]已知函数f (x)=ax2在区间 [1,2]上的平均变化率为,则f(x)在区间[-2,-1]上的平均变化率为 .
C
③
2.求函数在某一点处的导数
例3 求f (x)=x3-x在x=2处的导数.
【解】∵ Δy=f(2+Δx)-f(2)=(2+Δx)3-(2+Δx)-(23-2)
=(Δx)3+6(Δx)2+11Δx,
∴=(Δx)2+6Δx+11,
即f ′(2)=11.
训练题 [2019·吉林长春外国语学校高二检测]函数f(x)=x2-3在x=1处的瞬时变化率为 ( )
A. (Δx)2+2Δx B.Δx+2 C.2 D.4
C
3.根据导数定义求参数
例4 已知f (x)=ax3+3x2+2,若f ′(-1)=4,则a的值为( )
A. B. C. D.
【解析】因为Δy=f(x+Δx)-f(x)
=a(x+Δx)3+3(x+Δx)2+2-(ax3+3x2+2)
=3ax2·Δx+3ax(Δx)2+a(Δx)3+6x·Δx+3(Δx)2,
所以=3ax2+3ax·Δx+a(Δx)2+6x+3Δx,
所以 =3ax2+6x,即f ′(x)=3ax2+6x,
所以f ′(-1)=3a-6=4,解得a=.
【答案】C
4.根据导数定义求极限值
例5 [2020·山东兰陵二中高二检测]已知函数f (x)在x0处的导数为f ′(x0),则 等于 ( )
A.mf ′(x0) B.mf ′(x0)
C.f ′(x0) D.f ′(x0)
【答案】B
◆根据导数定义求极限值的方法
1.将已知极限式配凑成定义式的形式;
2.根据导数的定义得极限式的值.
C
2a
B
三、平均变化率、导数(瞬时变化率)的几何意义
1.曲线的割线及其应用
例6 已知曲线y=x2-1上两点A(2,3),B(2+Δx,3+Δy),当Δx=1时,割线AB的斜率是 ;当Δx=0.1时,割线AB的斜率是 .
【答案】5 4.1
训练题 设a=,b=2-,c=-2,则a,b,c的大小顺序为 ( )
A.a>b>c B.b>c>a C.c>a>b D.a>c>b
A
2.利用导数的几何意义描述函数图象
例7 一堆雪在融化过程中,其体积V(单位:m3)与融化时间t(单位:h)近似满足函数关系:V(t)=(H为常数),其图象如图所示.记这堆雪从融化开始到结束的平均融化速度为(m3/h).那么t1,t2,t3,t4中,瞬时融化速度等于(m3/h)的时刻是 .
【解析】由题意,可得平均融化速度
反映的是V(t)的图象与坐标轴交点连线的斜率,
观察可知t3处瞬时融化速度与平均融化速度一致.
【答案】t3
◆导数的几何意义
函数y=f(x)在x0处的导数f ′(x0)的几何意义,就是曲线y=f(x)在
点(x0,f(x0))处切线的斜率k,即k=f ′(x0)=
训练题
1.设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f ′(x)的图象可能为 ( )
D
A B C D
2.[2020·安徽合肥高二期末]函数y=f(x)的图象如图所示,
f ′(x)是函数f(x)的导函数,下列数值排序正确的是 ( )
A.f ′(2)
如图所示,则函数y=f(x)的图象可能是 ( )
A B C D
D
D
◆判断导函数的图象和函数图象的关系的方法
1.正则升,负则降.导数值为正时,函数图象呈上升趋势;导数值为负时,函数图象呈下降趋势.
2.大则陡,小则缓.导数的绝对值越大,函数图象越陡峭;导数的绝对值越小,函数图象越平缓.
3.求曲线的切线方程
例8 [2020·江西南昌二中高二期末]已知函数f(x)=x3+x-2.
(1)求曲线y=f(x)在点(2,8)处的切线方程;
(2)直线为曲线y=f(x)的切线,且经过原点,求直线的方程及切点坐标.
【解】
(1)因为f ′(2)=13,
所以曲线y=f(x)在点(2,8)处的切线方程为y-8=13(x-2),即13x-y-18=0.
(2)设切点为(x0, +x0-2),则f ′(x0)=3+1,
所以切线方程为y-(+x0-2)=(3+1)(x-x0).
因为切线过原点,
所以-(+x0-2)=-x0(3+1).
所以2=-2,解得x0=-1.
所以切点坐标为(-1,-4).
因为f ′(-1)=4,所以所求切线方程为y=4x.
◆利用导数的几何意义求曲线的切线方程的步骤
1. 求曲线y=f(x)在点P(x0,f(x0))处的切线方程的步骤
(1)求出函数y=f(x)在x0处的导数f ′(x0);
(2)根据直线方程的点斜式,得切线方程为
y-f(x0)=f ′(x0)(x-x0).
2. 求曲线y=f(x)过点P(x0,y0)的切线方程的步骤
(1)设切点为P′(x′,f(x′)),求切线的斜率k=f ′(x′),
写出切线方程(含参);
(2)把点P(x0,y0)的坐标代入切线方程,建立关于x′的方程,
解得x′的值,进而求出切线方程.
训练题
1.[2020·山东兰陵一中高二期末]已知f (x)=2x2,则曲线y=f(x)在点P(1,2)处的切线的倾斜角的正切值为 .
2.已知直线ax-by-2=0与曲线y=x3在点P(1,1)处的切线互相垂直,则的值为 ( )
A. B. C. D.
3.[2020·安徽合肥高二检测]如图所示,函数y=f(x)的图象在点P处的切线方程是,则=( )
A.1 B.2 C.3 D.4
D
4
A
4.已知曲线f(x)=.
(1)求曲线过点A(1,0)的切线方程;
(2)求曲线的斜率为的切线的方程.
5.已知直线l1为曲线y=x2+x-2在点(1,0)处的切线,l2为该曲线的另一条切线,且l1⊥l2.
(1)求直线l2的方程;
(2)求由直线l1,l2和x轴所围成的三角形的面积.
4.已知函数图象上某点处的切线方程求参数
例9 已知直线l:y=4x+a和曲线C:y=f (x)=x3-2x2+3相切,求a的值及切点坐标.
◆已知函数图象上某点处的切线方程求参数的方法
解题的关键是得到关于参数的方程(组),常根据以下结论列方程(组):
1.利用切点在曲线上可得关于参数的方程;
2.利用函数y=f(x)在x=x0处的导数即为曲线y=f(x)在点(x0,f(x0))处切线的斜率可得参数方程;
3.利用切点坐标满足切线方程可得参数方程.
训练题 [2020·广东东莞高二期末]若曲线y=x2+ax+b在点(1,1)处的切线为3x-y-2=0,则有 ( )
A.a=-1,b=1 B.a=1,b=-1
C.a=-2,b=1 D.a=2,b=-1
B
5.利用切线求最值问题
例10 已知直线x+2y-4=0与抛物线y2=2x相交于A,B两点,O是坐标原点,试在抛物线的曲线AOB上求一点P,使△ABP的面积最大.
◆利用切线求最值的一般思路
1.利用导数的几何意义可以解决一些与距离、面积相关的几何最值问题;
2.解决此类问题的关键是准确确定所求切线的位置,进而求出切点坐标;
3.曲线上点到直线的距离的最值问题常常转化为两平行线间的距离;
4.求切点可利用导数与待定系数法.
训练题 [2020·安徽芜湖高二期末]已知A,B,C三点在曲线y=上,其横坐标依次为1,m,4(1
B
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
