【课件】5.3 导数在研究函数中的应用 5.3.2 函数的极值与最大(小)值 第1课时(46页PPT) 数学-RJ·A-选择性必修第二册
文档属性
| 名称 | 【课件】5.3 导数在研究函数中的应用 5.3.2 函数的极值与最大(小)值 第1课时(46页PPT) 数学-RJ·A-选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 16:54:25 | ||
图片预览










文档简介
(共46张PPT)
数学-RJ·A-选择性必修第二册
5.3 导数在研究函数中的应用
5.3.2 函数的极值与最大(小)值
第1课时
第五章 一元函数的导数及其应用
学习目标
1.了解函数在某点取得极值的必要条件和充分条件.
2.能利用导数求某些函数的极大值、极小值.
3.体会导数与极值的关系.
重点:利用导数求函数的极值
难点:函数在某点取得极值的充要条件、含参问题
知识梳理
一、函数的极值
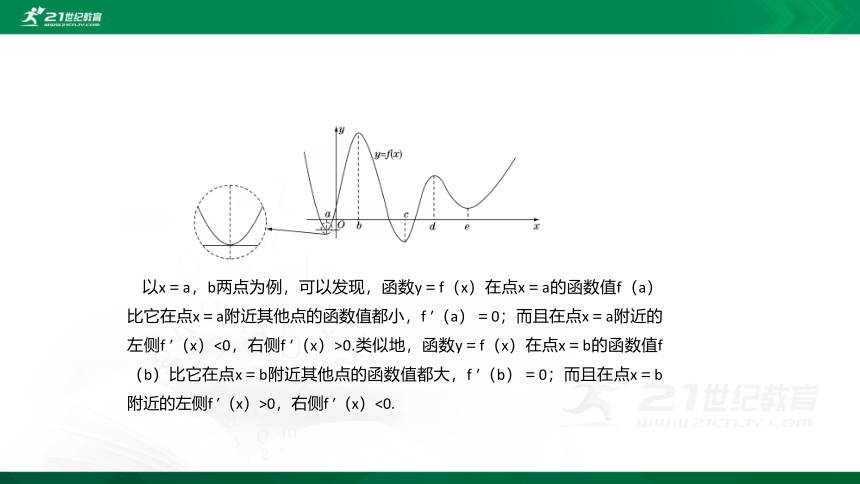
探究:如图所示,函数y=f(x)在x=a,b,c,d,e等点的函数值与这些点附近的函数值有什么关系?y=f(x)在这些点的导数值是多少?在这些点附近,y=f(x)的导数的正负性有什么规律?
以x=a,b两点为例,可以发现,函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f ′(a)=0;而且在点x=a附近的左侧f ′(x)<0,右侧f ′(x)>0.类似地,函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f ′(b)=0;而且在点x=b附近的左侧f ′(x)>0,右侧f ′(x)<0.
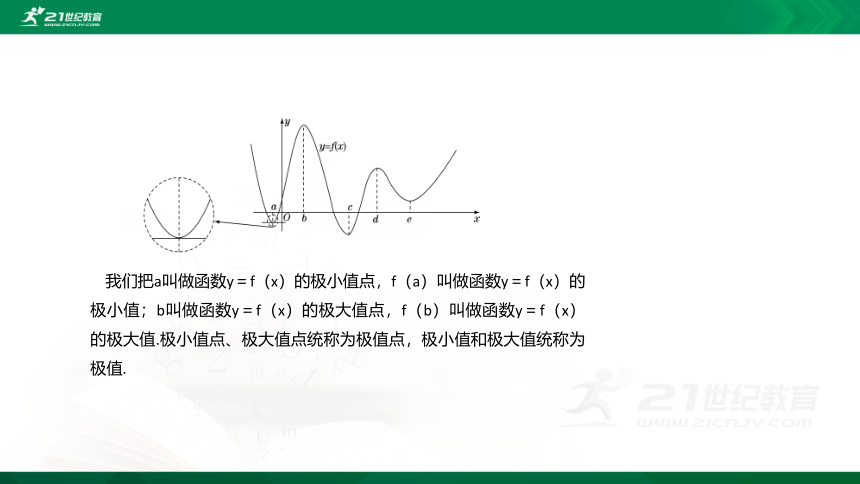
我们把a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值;b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.极小值点、极大值点统称为极值点,极小值和极大值统称为极值.
【注意】
(1)极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
(2)如果函数f(x)在[a,b]上有极值,那么它的极值点的分布是有规律的.相邻两个极大值点之间必有一个极小值点.同样,相邻两个极小值点之间必有一个极大值点.一般地,当函数f(x)在[a,b]上的图象连续且有有限个极值点时,函数f(x)在[a,b]内的极大值点、极小值点是交替出现的.
(3)极值点是单调性的转折点,因此若f(x)在(a,b)内有极值,则f(x)在(a,b)内不是单调函数.
思考:导数值为0的点一定是函数的极值点吗?
提示:导数值为0的点不一定是函数的极值点.例如,对于函数f(x)=x3,我们有f ′(x)=3x2.虽然f ′(0)=0,但由于无论x>0,还是x<0,恒有f ′(x)>0,即函数f(x)=x3是增函数,所以0不是函数=x3的极值点.一般地,函数y=f(x)在一点的导数值为0是函数y=f(x)在这点取极值的必要条件,而非充分条件.
一般地,可按如下方法求函数y=f(x)的极值:
解方程f ′(x)=0,当f ′(x0)=0时:
(1)如果在x0附近的左侧f ′(x)>0,右侧f ′(x)<0,那么f(x0)是极大值;
(2)如果在x0附近的左侧f ′(x)<0,右侧f ′(x)>0,那么f(x0)是极小值.
二、求函数极值的方法步骤
常考题型
一、函数极值的概念及判断
1.极值的概念
例1 (多选题)下列说法正确的是 ( )
A.若f(x)≥f(x0),则称f(x0)为f(x)的极小值,若f(x)≤f(x0),
则称f(x0)为f(x)的极大值
B.若f(x0)为f(x)的极大值,f(a)是函数的最大值,则f(x0)=f(a)
C.可导函数极值点的导数值为0,但导数值为0的点可能不是函数的极值点
D.极值点一定出现在定义区间的内部
E.若f(x)在区间(a,b)内有极值,则f(x)在(a,b)内一定不是单调函数
【解析】对于A,反例:设f(x)=,f(x)≥f(0)=0,因为0是区间[0,+∞)的端点,所以f(0)不是f(x)的极小值;设f(x)=-,f(x)≤f(0)=0,同理f(0)不是f(x)的极大值.所以A不正确.
对于B,由极值的定义知极大值不一定等于最大值,甚至有可能小于极小值,根据最大值的定义应该有f(x0)≤f(a),所以B不正确.
对于C,正确.
对于D,函数的极值是某个点的函数值,与它附近的函数值相比较是最大的或是最小的,端点不是函数的极值点,D正确.
对于E,在区间上单调的函数没有极值,E正确.
【答案】CDE
训练题 下列说法正确的是 ( )
A.若f ′(x0)=0,则f(x0)是函数f(x)的极值
B.若f(x0)是函数f(x)的极值,则f(x)在x0处有导数
C.函数f(x)至多有一个极大值和一个极小值
D.定义在R上的可导函数f(x),若方程f′(x)=0无实数解,则f(x)无极值
D
2.极值的判断
例2 已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),给出以下说法:
①函数f(x)在区间(1,+∞)上是增函数;
②函数f(x)在区间(-1,1)上单调递增;
③函数f(x)在x=-处取得极大值;
④函数f(x)在x=1处取得极小值.
其中正确的说法是 .
【解析】说法①,由图象知,当x∈(1,+∞)时,xf ′(x)>0,故f ′(x)>0,∴ f(x)在区间(1,+∞)上单调递增,①正确.
说法②,当x∈(-1,0)时,xf′(x)>0,故f′(x)<0;当x∈(0,1)时,xf′(x)<0,故f′(x)<0,故f(x)在(-1,0),(0,1)上是减函数,②不正确.
说法③,由②知f(x)在(-1,0)上单调递减,∴ x=-不是极值点,③不正确.
说法④,由①②知④是正确的.故填①④.
【答案】①④
◆极值的判断方法
1.若函数y=f(x)在区间(a,x0)上是增加的,在区间(x0,b)上是减少的,则x0是极大值点,f(x0)是极大值;若函数y=f(x)在区间(a,x0)上是减少的,在区间(x0,b)上是增加的,则x0是极小值点,f(x0)是极小值.
2.可导函数的导数值为0是函数有极值的必要不充分条件.可导函数y=f(x)在极值点处的导数值为0,但导数值为0的点不一定是极值点.
3.可导函数f(x)在x0取得极值的充要条件是f ′(x0)=0,且在x0左侧与右侧,f′(x)的符号不同.
4.若函数y=f(x)在(a,b)内单调,则y=f(x)在(a,b)内没有极值.
训练题
1.[2020·北京八中高二检测]如图是函数y=f(x)的
导函数y=f′(x)的图象,给出下列结论:
①-2是函数f(x)的极值点;②1是函数f(x)的极值点;
③f(x)在x=0处切线的斜率小于零;④f(x)在区间
(-2,2)上单调递增.其中正确结论的序号是 .(写出所有正确命题的序号)
2.已知函数y=x-ln(1+x2),则函数y=x-ln(1+x2)的极值情况是 ( )
A.有极小值 B.有极大值
C.既有极大值又有极小值 D.无极值
①④
D
二、求函数的极值
◆求函数的极值的一般步骤
(1)考虑函数的定义域并求导函数f′(x).
(2)解方程f′(x)=0,得方程的根x0(可能不止一个).
(3)检验方程f′(x)=0的每一个解x0左右两侧导函数的符号(即f(x)的单调性).
(4)确定极值点.
①若f′(x)在x0两侧的符号“左正右负”,则x0为极大值点;
②若f′(x)在x0两侧的符号“左负右正”,则x0为极小值点;
③若f′(x)在x0两侧的符号相同,则x0不是极值点.
训练题
1.设函数f(x)=xex,则 ( )
A.x=1为f(x)的极大值点
B.x=1为f(x)的极小值点
C.x=-1为f(x)的极大值点
D.x=-1为f(x)的极小值点
D
2.[2020·山东菏泽一中高二月考]已知二次函数f(x)=ax2+bx-1在x=-1处取得极值,且在点(0,-1)处的切线与直线2x-y=0平行.
(1)求f(x)的解析式;
(2)求函数g(x)=xf(x)+2x的极值.
2.讨论含参数的函数的极值
例4 设函数f(x)=ln(x+1)+a(x2-x),其中a∈R.讨论函数f(x)极值点的个数.
◆讨论含参数的函数的极值的一般思路
1.求函数定义域.
2.求导函数.
3.讨论导函数f′(x)的零点,若有零点,通过解方程f′(x)=0,得导函数的零点x0(可能不止一个),其中有的零点含参数.
4.在定义域内,讨论零点x0左右两侧的符号,得出函数单调性,讨论的依据有两个:
(1)看参数对f′(x)的零点是否有影响;
(2)看f′(x)在其零点附近的符号是否与参数有关.
5.得出函数的极值点.
训练题
1.[2020·安徽高三检测]已知函数f(x)=x2+(1+2a)ln x-(2a+2)x,若-≤a<0,则函数f(x)极值点的个数为 ( )
A.0或1 B.0或2 C.1或2 D.不确定
C
2.[2020·河南开封高二检测]已知函数f(x)=ln(x+1)+(a∈R).
(1)当a=1时,求函数f(x)的图象在点(0,f(0))处的切线方程;
(2)讨论函数f(x)的极值.
3.已知函数极值求参数值
例5 [2020·安徽六安一中高二检测]函数f(x)=x3+ax2+bx+a2+a在x=1处有极值7,则a= ( )
A.-3或3 B.3或-9 C.3 D.-3
【解析】f ′(x)=3x2+2ax+b,∴
解得
当a=3,b=-9时,f′(x)=3x2+6x-9=3(x-1)(x+3),当-31时,f′(x)>0,x=1是极小值点;当a=-3,b=3时,f′(x)=3x2-6x+3=3(x-1)2≥0,x=1不是极值点.∴ a=3.
【答案】C
◆已知函数极值求参数的方法
对于已知可导函数的极值求参数的问题,解题的切入点是极值存在的条件:极值点处的导数值为0;极值点两侧的导数值异号.具体步骤如下:
(1)求函数的导数f′(x);
(2)由极值点处的导数值为0和极值两个条件列出方程组,求解参数.
训练题
1.[2020·山东日照一中高三检测]等差数列{an}中的a1,a4039是函数f(x)=x3-4x2+6x-1的极值点,则log2a2020等于 .
2
2.[2015·广东中山一中等七校高三联考]已知函数f(x)=x(x-a)2,g(x)=-x2+(a-1)x+a(其中a∈R).如果函数y=f(x)和y=g(x)有相同的极值点,求a的值,并直接写出函数f(x)的单调区间.
4.已知函数极值求参数的取值范围
例6 [2014·湖南卷]已知常数a>0,函数f(x)=ln(1+ax).
(1)讨论f(x)在区间(0,+∞)上的单调性;
(2)若f(x)存在两个极值点x1,x2,且f(x1)+f(x2)>0,求a的取值范围.
◆已知函数极值求参数的取值范围的方法
1.已知一个函数,可以用单调性研究它的极值.反过来,已知函数的极值,可以确定函数解析式中的参数.
2.解这类问题,通常是围绕函数的导数等于零来建立关于参数的方程或不等式,从而求出参数的取值(范围).
3.需注意的是,可导函数在某点处的导数值等于零只是函数在该点处取得极值的必要条件,所以必须对求出的参数值进行检验,看是否符合函数取得极值的条件.
训练题
1.若函数f(x)=x2-2x+aln x有两个不同的极值点,则实数a的取值范围是 ( )
A.a>1 B.-1D
2.[2020·江苏南通高三期末]已知函数f(x)=ax3+3xln x-1(a∈R).
(1)当a=0时,求f(x)的极值;
(2)若f(x)在区间上有且只有一个极值点,求实数a的取值范围.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-选择性必修第二册
5.3 导数在研究函数中的应用
5.3.2 函数的极值与最大(小)值
第1课时
第五章 一元函数的导数及其应用
学习目标
1.了解函数在某点取得极值的必要条件和充分条件.
2.能利用导数求某些函数的极大值、极小值.
3.体会导数与极值的关系.
重点:利用导数求函数的极值
难点:函数在某点取得极值的充要条件、含参问题
知识梳理
一、函数的极值
探究:如图所示,函数y=f(x)在x=a,b,c,d,e等点的函数值与这些点附近的函数值有什么关系?y=f(x)在这些点的导数值是多少?在这些点附近,y=f(x)的导数的正负性有什么规律?
以x=a,b两点为例,可以发现,函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f ′(a)=0;而且在点x=a附近的左侧f ′(x)<0,右侧f ′(x)>0.类似地,函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f ′(b)=0;而且在点x=b附近的左侧f ′(x)>0,右侧f ′(x)<0.
我们把a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值;b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.极小值点、极大值点统称为极值点,极小值和极大值统称为极值.
【注意】
(1)极值反映了函数在某一点附近的大小情况,刻画了函数的局部性质.
(2)如果函数f(x)在[a,b]上有极值,那么它的极值点的分布是有规律的.相邻两个极大值点之间必有一个极小值点.同样,相邻两个极小值点之间必有一个极大值点.一般地,当函数f(x)在[a,b]上的图象连续且有有限个极值点时,函数f(x)在[a,b]内的极大值点、极小值点是交替出现的.
(3)极值点是单调性的转折点,因此若f(x)在(a,b)内有极值,则f(x)在(a,b)内不是单调函数.
思考:导数值为0的点一定是函数的极值点吗?
提示:导数值为0的点不一定是函数的极值点.例如,对于函数f(x)=x3,我们有f ′(x)=3x2.虽然f ′(0)=0,但由于无论x>0,还是x<0,恒有f ′(x)>0,即函数f(x)=x3是增函数,所以0不是函数=x3的极值点.一般地,函数y=f(x)在一点的导数值为0是函数y=f(x)在这点取极值的必要条件,而非充分条件.
一般地,可按如下方法求函数y=f(x)的极值:
解方程f ′(x)=0,当f ′(x0)=0时:
(1)如果在x0附近的左侧f ′(x)>0,右侧f ′(x)<0,那么f(x0)是极大值;
(2)如果在x0附近的左侧f ′(x)<0,右侧f ′(x)>0,那么f(x0)是极小值.
二、求函数极值的方法步骤
常考题型
一、函数极值的概念及判断
1.极值的概念
例1 (多选题)下列说法正确的是 ( )
A.若f(x)≥f(x0),则称f(x0)为f(x)的极小值,若f(x)≤f(x0),
则称f(x0)为f(x)的极大值
B.若f(x0)为f(x)的极大值,f(a)是函数的最大值,则f(x0)=f(a)
C.可导函数极值点的导数值为0,但导数值为0的点可能不是函数的极值点
D.极值点一定出现在定义区间的内部
E.若f(x)在区间(a,b)内有极值,则f(x)在(a,b)内一定不是单调函数
【解析】对于A,反例:设f(x)=,f(x)≥f(0)=0,因为0是区间[0,+∞)的端点,所以f(0)不是f(x)的极小值;设f(x)=-,f(x)≤f(0)=0,同理f(0)不是f(x)的极大值.所以A不正确.
对于B,由极值的定义知极大值不一定等于最大值,甚至有可能小于极小值,根据最大值的定义应该有f(x0)≤f(a),所以B不正确.
对于C,正确.
对于D,函数的极值是某个点的函数值,与它附近的函数值相比较是最大的或是最小的,端点不是函数的极值点,D正确.
对于E,在区间上单调的函数没有极值,E正确.
【答案】CDE
训练题 下列说法正确的是 ( )
A.若f ′(x0)=0,则f(x0)是函数f(x)的极值
B.若f(x0)是函数f(x)的极值,则f(x)在x0处有导数
C.函数f(x)至多有一个极大值和一个极小值
D.定义在R上的可导函数f(x),若方程f′(x)=0无实数解,则f(x)无极值
D
2.极值的判断
例2 已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),给出以下说法:
①函数f(x)在区间(1,+∞)上是增函数;
②函数f(x)在区间(-1,1)上单调递增;
③函数f(x)在x=-处取得极大值;
④函数f(x)在x=1处取得极小值.
其中正确的说法是 .
【解析】说法①,由图象知,当x∈(1,+∞)时,xf ′(x)>0,故f ′(x)>0,∴ f(x)在区间(1,+∞)上单调递增,①正确.
说法②,当x∈(-1,0)时,xf′(x)>0,故f′(x)<0;当x∈(0,1)时,xf′(x)<0,故f′(x)<0,故f(x)在(-1,0),(0,1)上是减函数,②不正确.
说法③,由②知f(x)在(-1,0)上单调递减,∴ x=-不是极值点,③不正确.
说法④,由①②知④是正确的.故填①④.
【答案】①④
◆极值的判断方法
1.若函数y=f(x)在区间(a,x0)上是增加的,在区间(x0,b)上是减少的,则x0是极大值点,f(x0)是极大值;若函数y=f(x)在区间(a,x0)上是减少的,在区间(x0,b)上是增加的,则x0是极小值点,f(x0)是极小值.
2.可导函数的导数值为0是函数有极值的必要不充分条件.可导函数y=f(x)在极值点处的导数值为0,但导数值为0的点不一定是极值点.
3.可导函数f(x)在x0取得极值的充要条件是f ′(x0)=0,且在x0左侧与右侧,f′(x)的符号不同.
4.若函数y=f(x)在(a,b)内单调,则y=f(x)在(a,b)内没有极值.
训练题
1.[2020·北京八中高二检测]如图是函数y=f(x)的
导函数y=f′(x)的图象,给出下列结论:
①-2是函数f(x)的极值点;②1是函数f(x)的极值点;
③f(x)在x=0处切线的斜率小于零;④f(x)在区间
(-2,2)上单调递增.其中正确结论的序号是 .(写出所有正确命题的序号)
2.已知函数y=x-ln(1+x2),则函数y=x-ln(1+x2)的极值情况是 ( )
A.有极小值 B.有极大值
C.既有极大值又有极小值 D.无极值
①④
D
二、求函数的极值
◆求函数的极值的一般步骤
(1)考虑函数的定义域并求导函数f′(x).
(2)解方程f′(x)=0,得方程的根x0(可能不止一个).
(3)检验方程f′(x)=0的每一个解x0左右两侧导函数的符号(即f(x)的单调性).
(4)确定极值点.
①若f′(x)在x0两侧的符号“左正右负”,则x0为极大值点;
②若f′(x)在x0两侧的符号“左负右正”,则x0为极小值点;
③若f′(x)在x0两侧的符号相同,则x0不是极值点.
训练题
1.设函数f(x)=xex,则 ( )
A.x=1为f(x)的极大值点
B.x=1为f(x)的极小值点
C.x=-1为f(x)的极大值点
D.x=-1为f(x)的极小值点
D
2.[2020·山东菏泽一中高二月考]已知二次函数f(x)=ax2+bx-1在x=-1处取得极值,且在点(0,-1)处的切线与直线2x-y=0平行.
(1)求f(x)的解析式;
(2)求函数g(x)=xf(x)+2x的极值.
2.讨论含参数的函数的极值
例4 设函数f(x)=ln(x+1)+a(x2-x),其中a∈R.讨论函数f(x)极值点的个数.
◆讨论含参数的函数的极值的一般思路
1.求函数定义域.
2.求导函数.
3.讨论导函数f′(x)的零点,若有零点,通过解方程f′(x)=0,得导函数的零点x0(可能不止一个),其中有的零点含参数.
4.在定义域内,讨论零点x0左右两侧的符号,得出函数单调性,讨论的依据有两个:
(1)看参数对f′(x)的零点是否有影响;
(2)看f′(x)在其零点附近的符号是否与参数有关.
5.得出函数的极值点.
训练题
1.[2020·安徽高三检测]已知函数f(x)=x2+(1+2a)ln x-(2a+2)x,若-≤a<0,则函数f(x)极值点的个数为 ( )
A.0或1 B.0或2 C.1或2 D.不确定
C
2.[2020·河南开封高二检测]已知函数f(x)=ln(x+1)+(a∈R).
(1)当a=1时,求函数f(x)的图象在点(0,f(0))处的切线方程;
(2)讨论函数f(x)的极值.
3.已知函数极值求参数值
例5 [2020·安徽六安一中高二检测]函数f(x)=x3+ax2+bx+a2+a在x=1处有极值7,则a= ( )
A.-3或3 B.3或-9 C.3 D.-3
【解析】f ′(x)=3x2+2ax+b,∴
解得
当a=3,b=-9时,f′(x)=3x2+6x-9=3(x-1)(x+3),当-3
【答案】C
◆已知函数极值求参数的方法
对于已知可导函数的极值求参数的问题,解题的切入点是极值存在的条件:极值点处的导数值为0;极值点两侧的导数值异号.具体步骤如下:
(1)求函数的导数f′(x);
(2)由极值点处的导数值为0和极值两个条件列出方程组,求解参数.
训练题
1.[2020·山东日照一中高三检测]等差数列{an}中的a1,a4039是函数f(x)=x3-4x2+6x-1的极值点,则log2a2020等于 .
2
2.[2015·广东中山一中等七校高三联考]已知函数f(x)=x(x-a)2,g(x)=-x2+(a-1)x+a(其中a∈R).如果函数y=f(x)和y=g(x)有相同的极值点,求a的值,并直接写出函数f(x)的单调区间.
4.已知函数极值求参数的取值范围
例6 [2014·湖南卷]已知常数a>0,函数f(x)=ln(1+ax).
(1)讨论f(x)在区间(0,+∞)上的单调性;
(2)若f(x)存在两个极值点x1,x2,且f(x1)+f(x2)>0,求a的取值范围.
◆已知函数极值求参数的取值范围的方法
1.已知一个函数,可以用单调性研究它的极值.反过来,已知函数的极值,可以确定函数解析式中的参数.
2.解这类问题,通常是围绕函数的导数等于零来建立关于参数的方程或不等式,从而求出参数的取值(范围).
3.需注意的是,可导函数在某点处的导数值等于零只是函数在该点处取得极值的必要条件,所以必须对求出的参数值进行检验,看是否符合函数取得极值的条件.
训练题
1.若函数f(x)=x2-2x+aln x有两个不同的极值点,则实数a的取值范围是 ( )
A.a>1 B.-1
2.[2020·江苏南通高三期末]已知函数f(x)=ax3+3xln x-1(a∈R).
(1)当a=0时,求f(x)的极值;
(2)若f(x)在区间上有且只有一个极值点,求实数a的取值范围.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
