【课件】5.3 导数在研究函数中的应用 5.3.2 函数的极值与最大(小)值 第2课时(73页PPT) 数学-RJ·A-选择性必修第二册
文档属性
| 名称 | 【课件】5.3 导数在研究函数中的应用 5.3.2 函数的极值与最大(小)值 第2课时(73页PPT) 数学-RJ·A-选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 17:16:49 | ||
图片预览











文档简介
(共73张PPT)
数学-RJ·A-选择性必修第二册
5.3 导数在研究函数中的应用
5.3.2 函数的极值与最大(小)值
第2课时
第五章 一元函数的导数及其应用
学习目标
1. 能利用导数求给定闭区间上不超过三次的多项式函数的最大值、最小值.
3.体会导数与最(大)小值的关系.
重点:利用导数求函数的最值
难点:含参问题、恒成立问题、用导数解决函数与方程问题
一、函数的最大(小)值
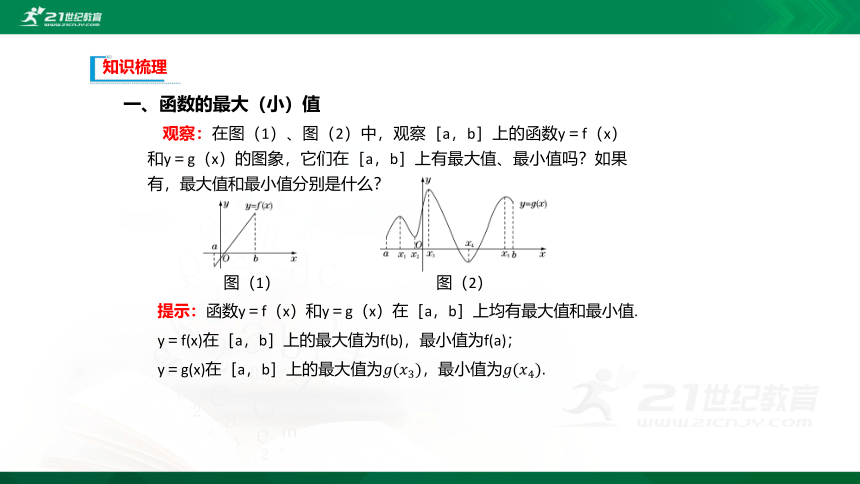
观察:在图(1)、图(2)中,观察[a,b]上的函数y=f(x)和y=g(x)的图象,它们在[a,b]上有最大值、最小值吗?如果有,最大值和最小值分别是什么?
图(1) 图(2)
提示:函数y=f(x)和y=g(x)在[a,b]上均有最大值和最小值.
y=f(x)在[a,b]上的最大值为f(b),最小值为f(a);
y=g(x)在[a,b]上的最大值为,最小值为.
知识梳理
一般地,如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
结合图(1)、图(2),以及函数极值中的例子,不难看出,只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值.
【注意】函数f(x)的图象在区间[a,b]上连续不断是f(x)在[a,b] 上存在最大值和最小值的充分不必要条件.如函数f(x)= 的图象(如图所示)虽然在[-1,1]上有间断点,但存在最大值和最小值.
在开区间(a,b)上函数的最值常见的有以下几种情况:
图(1)中的函数y=f(x)在(a,b)上有最大值而无最小值;
图(2)中的函数y=f(x)在(a,b)上有最小值而无最大值;
图(3)中的函数y=f(x)在(a,b)上既无最大值又无最小值;
图(4)中的函数y=f(x)在(a,b)上既有最大值又有最小值.
(1) (2) (3) (4)
一般地,求函数y=f(x)在区间[a,b]上的最大值与最小值的步骤如下:
(1)求函数y=f(x)在区间(a,b)上的极值;
(2)将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
二、求函数最值的方法步骤
一、求函数的最大(小)值
1.求函数的最大(小)值
例1 函数f(x)=ln(1+x)-x2在[0,2]上的最大值为 ,最小值为 .
【答案】ln 2- 0
常考题型
◆求函数f(x)在[a,b]上的最值的步骤
求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下:
1.求f(x)在[a,b]上的极值;
2.将f(x)的各极值与f(a),f(b)比较,其中最大的一个为最大值,最小的一个为最小值.
D
C
2.含参数函数的最值问题
例2 求函数f(x)=x3-4x+4在[0,a](a>0)上的最大值和最小值.
【解】f ′(x)=x2-4.令f′(x)=0,得x=2或x=-2(舍去).
因为0≤x≤a,所以当0所以f(x)在区间[0,a]上是减函数.
所以当x=a时,f(x)取得最小值f(a)=a3-4a+4;
当x=0时,f(x)取得最大值f(0)=4.
当a>2时,x,f′(x),f(x)的变化情况如下表:
x 0 (0,2) 2 (2,a)
f′(x) -4 - 0 +
f(x) 4 ? ?
从上表可知当x=2时,f(x)取得最小值f(2)=,f(x)的最大值为f(0)与f(a)中较大的一个.
所以当2当a>时,f(x)的最大值为f(a)=a3-4a+4.
综上,当0当2当a>时,f(x)min=,f(x)max=a3-4a+4.
◆含参数函数的最值问题
解决含参数函数的最值问题,明确参数的分类标准是关键,可以从导数为零时自变量的大小或通过比较函数值的大小等方面进行参数分界的确定.
训练题
1.已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a2=4b时,求函数f(x)+g(x)的单调区间,并求其在区间(-∞,-1]上的最大值.
解:(1)f ′(x)=2ax,g′(x)=3x2+b,
因为曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,所以f(1)=g(1),且f ′(1)=g′(1).
即a+1=1+b,且2a=3+b.解得a=3,b=3.
◆已知函数的最值求参数的值或参数范围的一般思路
(1)利用导数研究函数的单调性、极值和端点值;
(2)通过讨论和比较得出函数的最值;
(3)可以依据条件得含参数的方程或不等式,进而求得参数的值或取值范围,也可以通过分类讨论得出参数值或参数的取值范围.
2.设函数f(x)=ln x+ln(2-x)+ax(a>0).
(1)当a=1时,求f(x)的单调区间;
(2)若f(x)在(0,1]上的最大值为,求a的值.
二、利用导数研究不等式
◆构造函数法证明不等式
一般地,待证不等式的两边都含有同一个变量,可通过构造函数,转化为函数的最值问题来证明,其一般步骤如下:
1.移项,使不等式的一边为0,将另一边构造为“左减右”或“右减左”的函数;
2.利用导数研究所构造的函数的单调性;
3.借助构造函数的单调性可证结论成立.
训练题 1.已知函数f(x)=x--4ln x.
(1)求f(x)的单调递增区间;
(2)当02.[2020·河北石家庄高三模拟]已知函数f(x)=(x+b)(ex-a)(b>0),在点(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
(1)求a,b; (2)若m≤0,证明:f(x)≥mx2+x.
(1)解:a=1,b=1;
(2)证明:由(1)可知f(x)=(x+1)(ex-1),f(0)=0,
f(-1)=0,由m≤0,可得x≥mx2+x,
令g(x)=(x+1)(ex-1)-x,则g′(x)=(x+2)ex-2,
当x≤-2时,g′(x)=(x+2)ex-2<-2<0,
当x>-2时,设h(x)=g′(x)=(x+2)ex-2,
则h′(x)=(x+3)ex>0,
故函数g′(x)在(-2,+∞)上单调递增.
又g′(0)=0,所以当x∈(-∞,0)时,g′(x)<0,当x∈(0,+∞)时,g′(x)>0,
所以函数g(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增,
故g(x)≥g(0)=0,即(x+1)(ex-1)≥x≥mx2+x.
故f(x)≥mx2+x.
2.已知不等式恒成立求参数
例5 已知函数f(x)=ln x-ax2+x,a∈R.
(1)若a=2,求函数f(x)的单调递减区间;
(2)若关于x的不等式f(x)≤ax-1恒成立,求整数a的最小值.
◆已知不等式恒成立求参数的一般思路
1.一般将求解不等式恒成立问题转化为求函数最值问题;
2.含参数的函数不等式的恒成立问题,可构建新函数,再以导数为工具讨论新函数的单调性从而得到新函数的最值,最后由最值得到不等式成立;
3.求参数常用的方法有两种:
(1)移项合并构造新函数,求得新函数含有参数的最值,进而建立含参数的不等式求解;
(2)参变分离,把问题归结为不含参数的函数的值域问题.
A
【答案】
◆双变量恒成立与能成立问题的类型及解法
1.多变量不等式要先化为单变量不等式,然后构造新函数,转化为函数的最值问题,利用导数进行求解.
2.双变量的恒成立与能成立问题包含以下四种基本类型:
记区间D1,D2分别是函数y=f(x),y=g(x)定义域的子区间.
(1)x1∈D1, x2∈D2,f(x1)>g(x2)?f(x)min>g(x)max.其等价转化的基本思想是:函数y=f(x)的任一函数值均大于函数y=g(x)的任一函数值,只需f(x)min>g(x)max即可.
(2) x1∈D1,x2∈D2,f(x1)>g(x2)?f(x)min>g(x)min.其等价转化的基本思想是:函数y=f(x)的任一函数值大于函数y=g(x)的某些函数值,但并不要求大于函数y=g(x)的所有函数值,故只需f(x)min>g(x)min即可.
(3) x1∈D1, x2∈D2,f(x1)>g(x2)?f(x)max>g(x)max.其等价转化的基本思路是:函数y=f(x)的某些函数值大于函数y=g(x)的任一函数值,只要求y=f(x)有函数值大于y=g(x)的任一函数值即可,故只需f(x)max>g(x)max即可.
(4)x1∈D1,x2∈D2,f(x1)>g(x2)?f(x)max>g(x)min.其等价转化的基本思路是:函数y=f(x)的某些函数值大于函数y=g(x)的某些函数值,只要求有这样的函数值,不要求所有的函数值,故只需
f(x)max>g(x)min.
三、利用导数研究函数的零点问题
◆求函数的零点问题的一般思路
函数零点个数的判断,需利用函数的单调性和零点存在定理来判断,其一般步骤为:
1.要利用导数判断函数的单调性,确定其单调区间;
2.利用零点存在定理判断函数在每个单调区间上是否存在零点.要注意以下两点:
(1)选择怎样的点来计算其函数值且函数值异号是关键,可根据解析式的特点选择合适的点.
(2)证明函数在给定的范围上无零点,可利用放缩法把不易处理的函数转化为容易讨论的新函数来处理.
3.汇总得出结论.
训练题 [2020·安徽高三期末]已知函数f(x)=ax-2x(a>1).
(1)当a=e时,求证:f(x)-ln x+2x>2.
(2)讨论函数f(x)的零点个数.
2.已知函数的零点个数求参数的范围
例8 [2020·山东烟台一中高三月考]已知函数f(x)=ex-ax2,a∈R.
(1)当a=1时,求过点(0,1)且和曲线y=f(x)相切的直线方程;
(2)若函数f(x)在(0,+∞)上有两个不同的零点,求实数a的取值范围.
◆已知函数的零点个数求参数的范围的两种常用方法
1.对于函数的零点问题,可采用对原函数进行求导讨论其单调性、特殊点的函数值的符号的方法求解.
2.也可以采用对参数实行分离的方法,构造新函数,对其求导得出该函数的单调性和最值,可得参数的范围.
训练题 1.[2019·宁夏银川一中高三月考]设函数f(x)=mex-x2+3,其中m∈R.
(1)当m=0时,求函数h(x)=xf(x)的极值;
(2)若函数f(x)在区间[-2,4]上有两个零点,求m的取值范围.
解:(1)当m=0时,f(x)=-x2+3.
此时h(x)=xf(x)=-x3+3x,则h′(x)=-3x2+3.
当-10,当x<-1或x>1时,h′(x)<0,
∴ h(x)在(-∞,-1),(1,+∞)上单调递减,在(-1,1)上单调递增.
∴ h(x)有极小值h(-1)=-2,有极大值h(1)=2.
2.[2020·广东佛山一中高三月考]已知函数f(x)=-x3+ax2+4x的图象在x=1处的切线方程为y=-3x+4.
(1)求实数a的值;
(2)若方程f(x)-b=0有三个实数解,求实数b的取值范围.
解:(1)f ′(x)=-3x2+2ax+4,
f ′(1)=-3+2a+4=-3,解得a=-2;
(2)∵ f(x)-b=0,∴ f(x)=b.
由(1)得f ′(x)=-3x2-4x+4,令f ′(x)=0,解得x=或x=-2.
如图所示,当-20,f(x)在上单调递增,
当x<-2或x>时,f ′(x)<0,f(x)在(-∞,-2)和上单调递减,∴ f(x)在x=-2处取得极小值f(-2)=-8,在x=处取得极大值,
∴ 当-8◆与函数零点有关的不等式的证明的一般思路
1.对原不等式进行转化.
与函数零点有关的不等式的证明,可利用零点满足的等式,将要求证的不等式进行转化,一般要把含参数的不等式转化变为不含参数的不等式;
2.构造新函数,如果不等式含有多个变量,还要进一步转化为单变量,才能构造新函数;
3.利用导数讨论新函数的性质证明新转化的不等式是成立的.
训练题 1.[2020·安徽泗县一中高二期末]已知函数f(x)=ln x-2恰有两个零点,则实数m的取值范围是 ( )
A.(-e,0) B.(-e,+∞) C.(0,e) D.(-∞,e)
A
2.[2020·福建高三期末]已知函数f(x)=ax2ex-1(a≠0).
(1)求函数f(x)的单调区间;
(2)已知a>0且x∈[1,+∞),若函数f(x)没有零点,
求证:(x-1)(f(x)+1)≥x2ln x.
(1)解:f ′(x)=2ax·ex+ax2·ex=aexx(x+2).
当a>0时,令f ′(x)>0得x>0或x<-2;
令f ′(x)<0得-2∴ 函数f(x)的单调递增区间为(-∞,-2)和(0,+∞),单调递减区间为(-2,0).
当a<0时,令f ′(x)>0得-20或x<-2.
∴ 函数f(x)的单调递增区间为(-2,0),单调递减区间为(-∞,-2)和(0,+∞).
综上所述,当a>0时,函数f(x)的单调递增区间为(-∞,-2)和(0,+∞),单调递减区间为(-2,0);当a<0时,函数f(x)的单调递增区间为(-2,0),单调递减区间为(-∞,-2)和(0,+∞).
(2)证明:(方法一)函数f(x)在[1,+∞)上无零点,
即ax2ex-1=0在[1,+∞)无解,
则g(x)=x2ex与y=的图象在[1,+∞)无交点,
g′(x)=(2x+x2)ex>0,g(x)=x2ex在[1,+∞)上单调递增,
g(x)min=e,∴.
由(1)得f(x)在[1,+∞)上单调递增,f(x)≥f(1)=ae-1>0,
要证(x-1)(f(x)+1)≥x2ln x,即证(x-1)ax2ex≥x2ln x,
即证a(x-1)ex≥ln x,即证a(x-1)ex-ln x≥0.
令g(x)=a(x-1)ex-ln x,g′(x)=aex+a(x-1)ex-=aexx==>0,∴ g(x)在[1,+∞)上单调递增,
∴ g(x)≥g(1)=0,所以原不等式成立.
(方法二)函数f(x)在[1,+∞)上无零点,即ax2ex-1=0在[1,+∞)上无解,
则g(x)=x2ex与y=的图象在[1,+∞)上无交点,
g′(x)=(2x+x2)ex,g(x)=x2ex在[1,+∞)上单调递增,
g(x)min=e,∴.
要证(x-1)(f(x)+1)≥x2ln x,即证(x-1)ax2ex≥x2ln x,
即证a(x-1)ex≥ln x.
∵ a(x-1)ex>(x-1)ex=(x-1)ex-1≥(x-1),
∴ 只需证x-1≥ln x,即证x-1-ln x≥0,
令h(x)=x-1-ln x,h′(x)=1=≥0,
∴ h(x)在[1,+∞)上单调递增,∴ h(x)≥h(1)=0,
∴ 原不等式成立.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学-RJ·A-选择性必修第二册
5.3 导数在研究函数中的应用
5.3.2 函数的极值与最大(小)值
第2课时
第五章 一元函数的导数及其应用
学习目标
1. 能利用导数求给定闭区间上不超过三次的多项式函数的最大值、最小值.
3.体会导数与最(大)小值的关系.
重点:利用导数求函数的最值
难点:含参问题、恒成立问题、用导数解决函数与方程问题
一、函数的最大(小)值
观察:在图(1)、图(2)中,观察[a,b]上的函数y=f(x)和y=g(x)的图象,它们在[a,b]上有最大值、最小值吗?如果有,最大值和最小值分别是什么?
图(1) 图(2)
提示:函数y=f(x)和y=g(x)在[a,b]上均有最大值和最小值.
y=f(x)在[a,b]上的最大值为f(b),最小值为f(a);
y=g(x)在[a,b]上的最大值为,最小值为.
知识梳理
一般地,如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.
结合图(1)、图(2),以及函数极值中的例子,不难看出,只要把函数y=f(x)的所有极值连同端点的函数值进行比较,就可以求出函数的最大值与最小值.
【注意】函数f(x)的图象在区间[a,b]上连续不断是f(x)在[a,b] 上存在最大值和最小值的充分不必要条件.如函数f(x)= 的图象(如图所示)虽然在[-1,1]上有间断点,但存在最大值和最小值.
在开区间(a,b)上函数的最值常见的有以下几种情况:
图(1)中的函数y=f(x)在(a,b)上有最大值而无最小值;
图(2)中的函数y=f(x)在(a,b)上有最小值而无最大值;
图(3)中的函数y=f(x)在(a,b)上既无最大值又无最小值;
图(4)中的函数y=f(x)在(a,b)上既有最大值又有最小值.
(1) (2) (3) (4)
一般地,求函数y=f(x)在区间[a,b]上的最大值与最小值的步骤如下:
(1)求函数y=f(x)在区间(a,b)上的极值;
(2)将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.
二、求函数最值的方法步骤
一、求函数的最大(小)值
1.求函数的最大(小)值
例1 函数f(x)=ln(1+x)-x2在[0,2]上的最大值为 ,最小值为 .
【答案】ln 2- 0
常考题型
◆求函数f(x)在[a,b]上的最值的步骤
求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下:
1.求f(x)在[a,b]上的极值;
2.将f(x)的各极值与f(a),f(b)比较,其中最大的一个为最大值,最小的一个为最小值.
D
C
2.含参数函数的最值问题
例2 求函数f(x)=x3-4x+4在[0,a](a>0)上的最大值和最小值.
【解】f ′(x)=x2-4.令f′(x)=0,得x=2或x=-2(舍去).
因为0≤x≤a,所以当0
所以当x=a时,f(x)取得最小值f(a)=a3-4a+4;
当x=0时,f(x)取得最大值f(0)=4.
当a>2时,x,f′(x),f(x)的变化情况如下表:
x 0 (0,2) 2 (2,a)
f′(x) -4 - 0 +
f(x) 4 ? ?
从上表可知当x=2时,f(x)取得最小值f(2)=,f(x)的最大值为f(0)与f(a)中较大的一个.
所以当2
综上,当0
◆含参数函数的最值问题
解决含参数函数的最值问题,明确参数的分类标准是关键,可以从导数为零时自变量的大小或通过比较函数值的大小等方面进行参数分界的确定.
训练题
1.已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,求a,b的值;
(2)当a2=4b时,求函数f(x)+g(x)的单调区间,并求其在区间(-∞,-1]上的最大值.
解:(1)f ′(x)=2ax,g′(x)=3x2+b,
因为曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处具有公共切线,所以f(1)=g(1),且f ′(1)=g′(1).
即a+1=1+b,且2a=3+b.解得a=3,b=3.
◆已知函数的最值求参数的值或参数范围的一般思路
(1)利用导数研究函数的单调性、极值和端点值;
(2)通过讨论和比较得出函数的最值;
(3)可以依据条件得含参数的方程或不等式,进而求得参数的值或取值范围,也可以通过分类讨论得出参数值或参数的取值范围.
2.设函数f(x)=ln x+ln(2-x)+ax(a>0).
(1)当a=1时,求f(x)的单调区间;
(2)若f(x)在(0,1]上的最大值为,求a的值.
二、利用导数研究不等式
◆构造函数法证明不等式
一般地,待证不等式的两边都含有同一个变量,可通过构造函数,转化为函数的最值问题来证明,其一般步骤如下:
1.移项,使不等式的一边为0,将另一边构造为“左减右”或“右减左”的函数;
2.利用导数研究所构造的函数的单调性;
3.借助构造函数的单调性可证结论成立.
训练题 1.已知函数f(x)=x--4ln x.
(1)求f(x)的单调递增区间;
(2)当0
(1)求a,b; (2)若m≤0,证明:f(x)≥mx2+x.
(1)解:a=1,b=1;
(2)证明:由(1)可知f(x)=(x+1)(ex-1),f(0)=0,
f(-1)=0,由m≤0,可得x≥mx2+x,
令g(x)=(x+1)(ex-1)-x,则g′(x)=(x+2)ex-2,
当x≤-2时,g′(x)=(x+2)ex-2<-2<0,
当x>-2时,设h(x)=g′(x)=(x+2)ex-2,
则h′(x)=(x+3)ex>0,
故函数g′(x)在(-2,+∞)上单调递增.
又g′(0)=0,所以当x∈(-∞,0)时,g′(x)<0,当x∈(0,+∞)时,g′(x)>0,
所以函数g(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增,
故g(x)≥g(0)=0,即(x+1)(ex-1)≥x≥mx2+x.
故f(x)≥mx2+x.
2.已知不等式恒成立求参数
例5 已知函数f(x)=ln x-ax2+x,a∈R.
(1)若a=2,求函数f(x)的单调递减区间;
(2)若关于x的不等式f(x)≤ax-1恒成立,求整数a的最小值.
◆已知不等式恒成立求参数的一般思路
1.一般将求解不等式恒成立问题转化为求函数最值问题;
2.含参数的函数不等式的恒成立问题,可构建新函数,再以导数为工具讨论新函数的单调性从而得到新函数的最值,最后由最值得到不等式成立;
3.求参数常用的方法有两种:
(1)移项合并构造新函数,求得新函数含有参数的最值,进而建立含参数的不等式求解;
(2)参变分离,把问题归结为不含参数的函数的值域问题.
A
【答案】
◆双变量恒成立与能成立问题的类型及解法
1.多变量不等式要先化为单变量不等式,然后构造新函数,转化为函数的最值问题,利用导数进行求解.
2.双变量的恒成立与能成立问题包含以下四种基本类型:
记区间D1,D2分别是函数y=f(x),y=g(x)定义域的子区间.
(1)x1∈D1, x2∈D2,f(x1)>g(x2)?f(x)min>g(x)max.其等价转化的基本思想是:函数y=f(x)的任一函数值均大于函数y=g(x)的任一函数值,只需f(x)min>g(x)max即可.
(2) x1∈D1,x2∈D2,f(x1)>g(x2)?f(x)min>g(x)min.其等价转化的基本思想是:函数y=f(x)的任一函数值大于函数y=g(x)的某些函数值,但并不要求大于函数y=g(x)的所有函数值,故只需f(x)min>g(x)min即可.
(3) x1∈D1, x2∈D2,f(x1)>g(x2)?f(x)max>g(x)max.其等价转化的基本思路是:函数y=f(x)的某些函数值大于函数y=g(x)的任一函数值,只要求y=f(x)有函数值大于y=g(x)的任一函数值即可,故只需f(x)max>g(x)max即可.
(4)x1∈D1,x2∈D2,f(x1)>g(x2)?f(x)max>g(x)min.其等价转化的基本思路是:函数y=f(x)的某些函数值大于函数y=g(x)的某些函数值,只要求有这样的函数值,不要求所有的函数值,故只需
f(x)max>g(x)min.
三、利用导数研究函数的零点问题
◆求函数的零点问题的一般思路
函数零点个数的判断,需利用函数的单调性和零点存在定理来判断,其一般步骤为:
1.要利用导数判断函数的单调性,确定其单调区间;
2.利用零点存在定理判断函数在每个单调区间上是否存在零点.要注意以下两点:
(1)选择怎样的点来计算其函数值且函数值异号是关键,可根据解析式的特点选择合适的点.
(2)证明函数在给定的范围上无零点,可利用放缩法把不易处理的函数转化为容易讨论的新函数来处理.
3.汇总得出结论.
训练题 [2020·安徽高三期末]已知函数f(x)=ax-2x(a>1).
(1)当a=e时,求证:f(x)-ln x+2x>2.
(2)讨论函数f(x)的零点个数.
2.已知函数的零点个数求参数的范围
例8 [2020·山东烟台一中高三月考]已知函数f(x)=ex-ax2,a∈R.
(1)当a=1时,求过点(0,1)且和曲线y=f(x)相切的直线方程;
(2)若函数f(x)在(0,+∞)上有两个不同的零点,求实数a的取值范围.
◆已知函数的零点个数求参数的范围的两种常用方法
1.对于函数的零点问题,可采用对原函数进行求导讨论其单调性、特殊点的函数值的符号的方法求解.
2.也可以采用对参数实行分离的方法,构造新函数,对其求导得出该函数的单调性和最值,可得参数的范围.
训练题 1.[2019·宁夏银川一中高三月考]设函数f(x)=mex-x2+3,其中m∈R.
(1)当m=0时,求函数h(x)=xf(x)的极值;
(2)若函数f(x)在区间[-2,4]上有两个零点,求m的取值范围.
解:(1)当m=0时,f(x)=-x2+3.
此时h(x)=xf(x)=-x3+3x,则h′(x)=-3x2+3.
当-1
∴ h(x)在(-∞,-1),(1,+∞)上单调递减,在(-1,1)上单调递增.
∴ h(x)有极小值h(-1)=-2,有极大值h(1)=2.
2.[2020·广东佛山一中高三月考]已知函数f(x)=-x3+ax2+4x的图象在x=1处的切线方程为y=-3x+4.
(1)求实数a的值;
(2)若方程f(x)-b=0有三个实数解,求实数b的取值范围.
解:(1)f ′(x)=-3x2+2ax+4,
f ′(1)=-3+2a+4=-3,解得a=-2;
(2)∵ f(x)-b=0,∴ f(x)=b.
由(1)得f ′(x)=-3x2-4x+4,令f ′(x)=0,解得x=或x=-2.
如图所示,当-2
当x<-2或x>时,f ′(x)<0,f(x)在(-∞,-2)和上单调递减,∴ f(x)在x=-2处取得极小值f(-2)=-8,在x=处取得极大值,
∴ 当-8
1.对原不等式进行转化.
与函数零点有关的不等式的证明,可利用零点满足的等式,将要求证的不等式进行转化,一般要把含参数的不等式转化变为不含参数的不等式;
2.构造新函数,如果不等式含有多个变量,还要进一步转化为单变量,才能构造新函数;
3.利用导数讨论新函数的性质证明新转化的不等式是成立的.
训练题 1.[2020·安徽泗县一中高二期末]已知函数f(x)=ln x-2恰有两个零点,则实数m的取值范围是 ( )
A.(-e,0) B.(-e,+∞) C.(0,e) D.(-∞,e)
A
2.[2020·福建高三期末]已知函数f(x)=ax2ex-1(a≠0).
(1)求函数f(x)的单调区间;
(2)已知a>0且x∈[1,+∞),若函数f(x)没有零点,
求证:(x-1)(f(x)+1)≥x2ln x.
(1)解:f ′(x)=2ax·ex+ax2·ex=aexx(x+2).
当a>0时,令f ′(x)>0得x>0或x<-2;
令f ′(x)<0得-2
当a<0时,令f ′(x)>0得-2
∴ 函数f(x)的单调递增区间为(-2,0),单调递减区间为(-∞,-2)和(0,+∞).
综上所述,当a>0时,函数f(x)的单调递增区间为(-∞,-2)和(0,+∞),单调递减区间为(-2,0);当a<0时,函数f(x)的单调递增区间为(-2,0),单调递减区间为(-∞,-2)和(0,+∞).
(2)证明:(方法一)函数f(x)在[1,+∞)上无零点,
即ax2ex-1=0在[1,+∞)无解,
则g(x)=x2ex与y=的图象在[1,+∞)无交点,
g′(x)=(2x+x2)ex>0,g(x)=x2ex在[1,+∞)上单调递增,
g(x)min=e,∴
由(1)得f(x)在[1,+∞)上单调递增,f(x)≥f(1)=ae-1>0,
要证(x-1)(f(x)+1)≥x2ln x,即证(x-1)ax2ex≥x2ln x,
即证a(x-1)ex≥ln x,即证a(x-1)ex-ln x≥0.
令g(x)=a(x-1)ex-ln x,g′(x)=aex+a(x-1)ex-=aexx==>0,∴ g(x)在[1,+∞)上单调递增,
∴ g(x)≥g(1)=0,所以原不等式成立.
(方法二)函数f(x)在[1,+∞)上无零点,即ax2ex-1=0在[1,+∞)上无解,
则g(x)=x2ex与y=的图象在[1,+∞)上无交点,
g′(x)=(2x+x2)ex,g(x)=x2ex在[1,+∞)上单调递增,
g(x)min=e,∴
要证(x-1)(f(x)+1)≥x2ln x,即证(x-1)ax2ex≥x2ln x,
即证a(x-1)ex≥ln x.
∵ a(x-1)ex>(x-1)ex=(x-1)ex-1≥(x-1),
∴ 只需证x-1≥ln x,即证x-1-ln x≥0,
令h(x)=x-1-ln x,h′(x)=1=≥0,
∴ h(x)在[1,+∞)上单调递增,∴ h(x)≥h(1)=0,
∴ 原不等式成立.
知易行难,重在行动
千里之行,始于足下
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
