4.1.2认识三角形(2) 课件(共28张PPT)
文档属性
| 名称 | 4.1.2认识三角形(2) 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 07:24:20 | ||
图片预览




文档简介
(共28张PPT)
4.1.2认识三角形(2)
第四章 三角形
七年级数学下册同步(北师大版)
学习目标
1.了解按边的相等关系对三角形进行分类;
2.理解三角形任何两边之和大于第三边与任意两边之差小于第三边的性质,并会初步运用这些性质来解决问题;
3.在探索三角形三边关系的过程中,通过观察、实验、推理、交流等活动,发展空间观念、推理能力和有条理的表达能力.
导入新课
所有内角都是锐角的三角形———
有一个内角是直角的三角形———
锐角三角形
直角三角形
钝角三角形
有一个内角是钝角的三角形———
导入新课
锐角三角形
直角三角形
钝角三角形
⑦
②
①
③
④
⑤
⑥
①
②
③
④
⑤
⑥
⑦
讲授新课
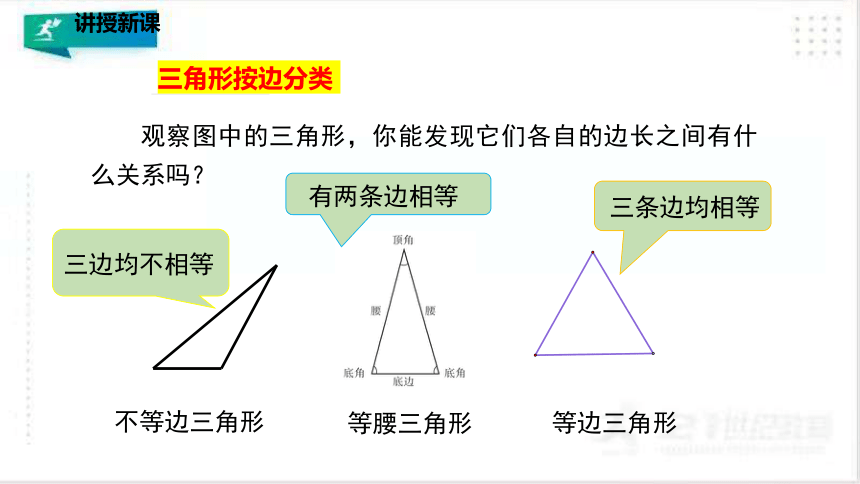
三角形按边分类
观察图中的三角形,你能发现它们各自的边长之间有什么关系吗?
不等边三角形
等腰三角形
等边三角形
三边均不相等
有两条边相等
三条边均相等
讲授新课
腰
等腰三角形
底边
顶角
底角
有两条边相等
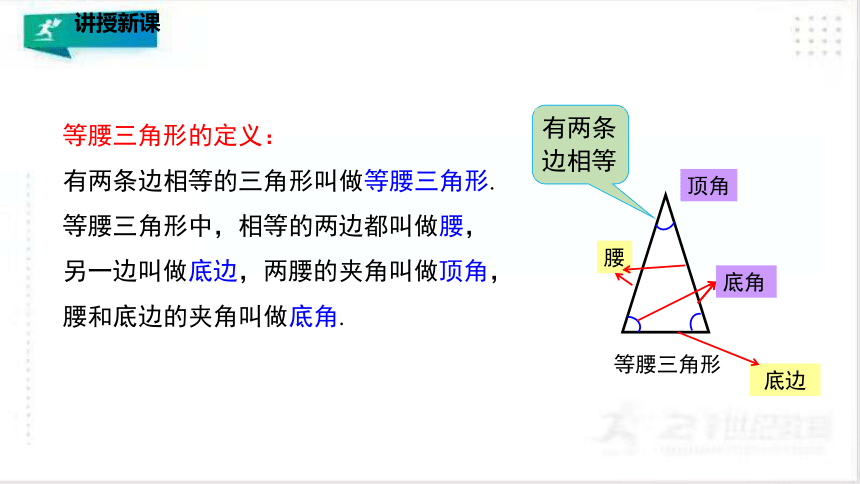
等腰三角形的定义:
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,
另一边叫做底边,两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
讲授新课
等边三角形
三条边均相等
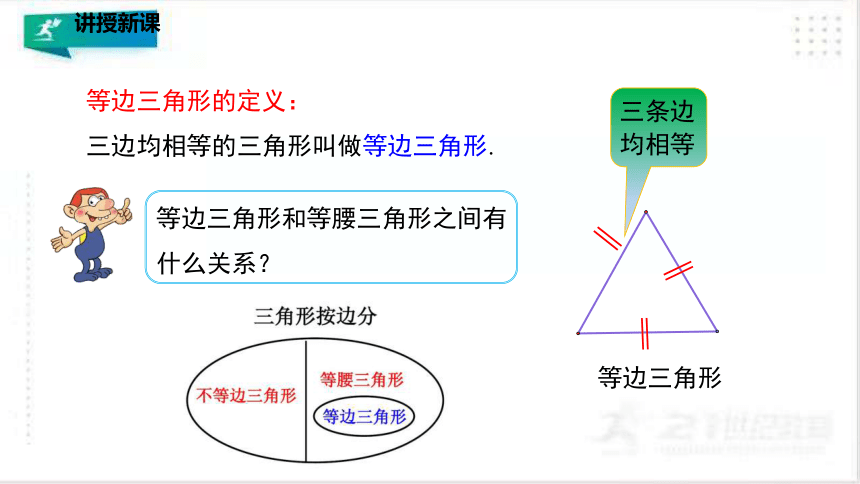
等边三角形的定义:
三边均相等的三角形叫做等边三角形.
等边三角形和等腰三角形之间有什么关系?
讲授新课
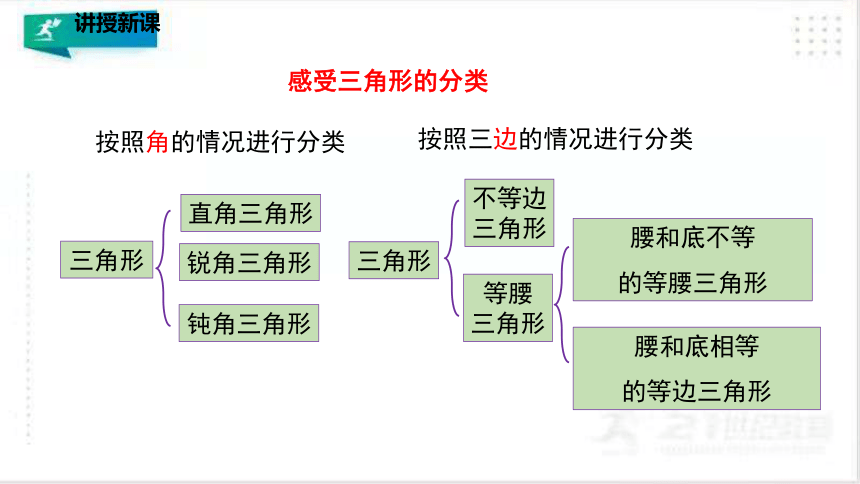
感受三角形的分类
按照角的情况进行分类
直角三角形
锐角三角形
钝角三角形
三角形
按照三边的情况进行分类
三角形
不等边
三角形
等腰
三角形
腰和底不等
的等腰三角形
腰和底相等
的等边三角形
讲授新课
三角形的三边关系
(1)元宵节的晚上,房梁上亮起了彩灯(如图),装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由.
(2)在一个三角形中,任意两边之和与第三边的长度有怎样的关系?为什么?
讲授新课
准备5根木棒长分别为3cm,4cm,5cm,6cm,9cm,任意取出3根首尾相接搭三角形,并填表:
选择的长度 能否搭出三角形 能 不能
3cm,4cm,5cm √
选择的长度 能否搭出三角形 能 不能
讲授新课
准备5根木棒长分别为3cm,4cm,5cm,6cm,9cm,任意取出3根首尾相接搭三角形,并填表:
选择的长度 能否搭出三角形 能 不能
3cm,4cm,5cm √
3cm,4cm,6cm √
3cm,4cm,9cm √
3cm,5cm,6cm √
3cm,5cm,9cm √
选择的长度 能否搭出三角形 能 不能
3cm,6cm,9cm √
4cm,5cm,6cm √
4cm,5cm,9cm √
4cm,6cm,9cm √
5cm,6cm,9cm √
讲授新课
选出可以搭出三角形的数据,请你计算比较,你发现了什么?
4cm 6cm 9cm
5cm 6cm 9cm
a b c
3cm 4cm 5cm
3cm 4cm 6cm
3cm 5cm 6cm
4cm 5cm 6cm
(1)计算并比较:
a+b____c; b+c____a ; c+a____b
a-b____c ; b-c____a; c-a____b
(2)通过以上的计算你认为三角形的三边存在怎样的关系?
>
>
>
<
<
<
归纳总结
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
三条线段能够组成三角形的判定条件
两边之差<第三边<两边之和
AB-AC< BC <AB+AC
讲授新课
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
例1 有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
讲授新课
例2一个等腰三角形的两边长分别为4,8,则它的周长为( )
A.12 B.16
C.20 D.16或20
C
经典易错:
对于等腰三角形的题目一定要检验是否能组成三角形!
讲授新课
例3 若a,b,c是△ABC的三边长,
化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
根据两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负是经典高频题型.
当堂检测
1. 如图,在△ABC中,BC=BA,点D在AB上,且AC=CD=DB,则图中的等腰三角形有( )
A.1个
B.2个
C.3个
D.4个
C
当堂检测
2. 设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间关系的是( )
C
当堂检测
3.若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.14 B.10
C.3 D.2
B
4.已知a,b,c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )
A.2a+2b-2c B.2a+2b
C.2c D.0
D
当堂检测
5.两根木棒长分别为6 cm和7 cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒的长为偶数,那么第三根木棒长的取值情况有( )种.
A.3 B.4 C.5 D.6
D
6.一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
A
当堂检测
7.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线段为边长可以构成____个三角形.
3
8. 如图,若等腰三角形的两腰长分别为x cm和(2x-6)cm,且周长为17 cm,则第三边的长为 cm.
5
当堂检测
9.判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;
(3)5cm、6cm、10cm.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
当堂检测
10.已知等腰三角形的周长为18cm,如果一边长等于4cm,求另两边的长?
解:若底边长为4cm,设腰长为x cm,
则2x+4=18,解得x=7.
若一条腰长为4cm,设底边长为x cm,
则2×4+x=18,解得x=10.
因为4+4<10,所以4cm为腰不能构成三角形.
所以三角形另外两个边长都是7cm.
当堂检测
11.等腰三角形中,周长为18cm.
(1)如果腰长是底边长的2倍,求各边长;
(2)如果一边长为4cm,求另两边长.
解:(1)设等腰三角形的底边长为xcm,则腰长为2xcm.根据题意,
得:x+2x+2x=18;解方程,得x=3.6
故三角形的三边长为3.6cm,7.2cm,7.2cm.
当堂检测
(2)①若底边长为4cm,设腰长为xcm,则有:x+x+4=18
解方程,得x=7cm.
②若一条腰长为4cm,设底边长为xcm,则有:4+4+x=18
解方程,得x=10.
∵4+4<10, ∴以4为腰不能构成三角形,
故三角形的另两边长都为7cm.
11.等腰三角形中,周长为18cm.
(1)如果腰长是底边长的2倍,求各边长;
(2)如果一边长为4cm,求另两边长.
课堂小结
三角形中边的关系
三角形按边分类
不等边三角形
等腰三角形
三角形的三边关系
任意两边之和大于第三边
任意两边之差小于第三边
腰和底边不相等的等腰三角形
等边三角形
https://www.21cnjy.com/help/help_extract.php
4.1.2认识三角形(2)
第四章 三角形
七年级数学下册同步(北师大版)
学习目标
1.了解按边的相等关系对三角形进行分类;
2.理解三角形任何两边之和大于第三边与任意两边之差小于第三边的性质,并会初步运用这些性质来解决问题;
3.在探索三角形三边关系的过程中,通过观察、实验、推理、交流等活动,发展空间观念、推理能力和有条理的表达能力.
导入新课
所有内角都是锐角的三角形———
有一个内角是直角的三角形———
锐角三角形
直角三角形
钝角三角形
有一个内角是钝角的三角形———
导入新课
锐角三角形
直角三角形
钝角三角形
⑦
②
①
③
④
⑤
⑥
①
②
③
④
⑤
⑥
⑦
讲授新课
三角形按边分类
观察图中的三角形,你能发现它们各自的边长之间有什么关系吗?
不等边三角形
等腰三角形
等边三角形
三边均不相等
有两条边相等
三条边均相等
讲授新课
腰
等腰三角形
底边
顶角
底角
有两条边相等
等腰三角形的定义:
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边都叫做腰,
另一边叫做底边,两腰的夹角叫做顶角,
腰和底边的夹角叫做底角.
讲授新课
等边三角形
三条边均相等
等边三角形的定义:
三边均相等的三角形叫做等边三角形.
等边三角形和等腰三角形之间有什么关系?
讲授新课
感受三角形的分类
按照角的情况进行分类
直角三角形
锐角三角形
钝角三角形
三角形
按照三边的情况进行分类
三角形
不等边
三角形
等腰
三角形
腰和底不等
的等腰三角形
腰和底相等
的等边三角形
讲授新课
三角形的三边关系
(1)元宵节的晚上,房梁上亮起了彩灯(如图),装有黄色彩灯的电线与装有红色彩灯的电线哪根长呢?说明你的理由.
(2)在一个三角形中,任意两边之和与第三边的长度有怎样的关系?为什么?
讲授新课
准备5根木棒长分别为3cm,4cm,5cm,6cm,9cm,任意取出3根首尾相接搭三角形,并填表:
选择的长度 能否搭出三角形 能 不能
3cm,4cm,5cm √
选择的长度 能否搭出三角形 能 不能
讲授新课
准备5根木棒长分别为3cm,4cm,5cm,6cm,9cm,任意取出3根首尾相接搭三角形,并填表:
选择的长度 能否搭出三角形 能 不能
3cm,4cm,5cm √
3cm,4cm,6cm √
3cm,4cm,9cm √
3cm,5cm,6cm √
3cm,5cm,9cm √
选择的长度 能否搭出三角形 能 不能
3cm,6cm,9cm √
4cm,5cm,6cm √
4cm,5cm,9cm √
4cm,6cm,9cm √
5cm,6cm,9cm √
讲授新课
选出可以搭出三角形的数据,请你计算比较,你发现了什么?
4cm 6cm 9cm
5cm 6cm 9cm
a b c
3cm 4cm 5cm
3cm 4cm 6cm
3cm 5cm 6cm
4cm 5cm 6cm
(1)计算并比较:
a+b____c; b+c____a ; c+a____b
a-b____c ; b-c____a; c-a____b
(2)通过以上的计算你认为三角形的三边存在怎样的关系?
>
>
>
<
<
<
归纳总结
三角形任意两边之和大于第三边.
三角形任意两边之差小于第三边.
三条线段能够组成三角形的判定条件
两边之差<第三边<两边之和
AB-AC< BC <AB+AC
讲授新课
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
例1 有两根长度分别为5cm和8cm的木棒,用长度为2cm的木棒与它们能摆成三角形吗?为什么?长度为13cm的木棒呢?
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.
取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
讲授新课
例2一个等腰三角形的两边长分别为4,8,则它的周长为( )
A.12 B.16
C.20 D.16或20
C
经典易错:
对于等腰三角形的题目一定要检验是否能组成三角形!
讲授新课
例3 若a,b,c是△ABC的三边长,
化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,得
a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
根据两边之和大于第三边,两边之差小于第三边,来判定绝对值里的式子的正负是经典高频题型.
当堂检测
1. 如图,在△ABC中,BC=BA,点D在AB上,且AC=CD=DB,则图中的等腰三角形有( )
A.1个
B.2个
C.3个
D.4个
C
当堂检测
2. 设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间关系的是( )
C
当堂检测
3.若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.14 B.10
C.3 D.2
B
4.已知a,b,c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )
A.2a+2b-2c B.2a+2b
C.2c D.0
D
当堂检测
5.两根木棒长分别为6 cm和7 cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒的长为偶数,那么第三根木棒长的取值情况有( )种.
A.3 B.4 C.5 D.6
D
6.一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7
C.-3<x<11 D.x>3
A
当堂检测
7.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线段为边长可以构成____个三角形.
3
8. 如图,若等腰三角形的两腰长分别为x cm和(2x-6)cm,且周长为17 cm,则第三边的长为 cm.
5
当堂检测
9.判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;
(3)5cm、6cm、10cm.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
当堂检测
10.已知等腰三角形的周长为18cm,如果一边长等于4cm,求另两边的长?
解:若底边长为4cm,设腰长为x cm,
则2x+4=18,解得x=7.
若一条腰长为4cm,设底边长为x cm,
则2×4+x=18,解得x=10.
因为4+4<10,所以4cm为腰不能构成三角形.
所以三角形另外两个边长都是7cm.
当堂检测
11.等腰三角形中,周长为18cm.
(1)如果腰长是底边长的2倍,求各边长;
(2)如果一边长为4cm,求另两边长.
解:(1)设等腰三角形的底边长为xcm,则腰长为2xcm.根据题意,
得:x+2x+2x=18;解方程,得x=3.6
故三角形的三边长为3.6cm,7.2cm,7.2cm.
当堂检测
(2)①若底边长为4cm,设腰长为xcm,则有:x+x+4=18
解方程,得x=7cm.
②若一条腰长为4cm,设底边长为xcm,则有:4+4+x=18
解方程,得x=10.
∵4+4<10, ∴以4为腰不能构成三角形,
故三角形的另两边长都为7cm.
11.等腰三角形中,周长为18cm.
(1)如果腰长是底边长的2倍,求各边长;
(2)如果一边长为4cm,求另两边长.
课堂小结
三角形中边的关系
三角形按边分类
不等边三角形
等腰三角形
三角形的三边关系
任意两边之和大于第三边
任意两边之差小于第三边
腰和底边不相等的等腰三角形
等边三角形
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
