华东师大版数学九年级下册 26.3实践与探索练习试题 (word版含答案)
文档属性
| 名称 | 华东师大版数学九年级下册 26.3实践与探索练习试题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 231.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 19:14:38 | ||
图片预览



文档简介
26.3实践与探索练习试题
(限时70分钟 满分120分)
一、选择(本题共计8小题,每题5分,共计40分)
1.如图,点 在二次函数 的图象上,则方程 解的一个近似值可能是( )
A.2.18 B.2.68 C.-0.51 D.2.45
2.已知二次函数y=ax2+bx+1,一次函数y=k(x-1)-,若它们的图象对于任意的非零实数k都只有一个公共点,则a,b的值分别为( )
A.a=1,b=2 B.a=1,b=-2 C.a=-1,b=2 D.a=-1,b=-2
3.对于二次函数y=x2﹣4x+7的图象,下列说法正确的是( )
A.开口向下 B.对称轴是x=﹣2
C.顶点坐标是(2,3) D.与x轴有两个交点
4.已知二次函数y=ax2+bx+c( )的图像如图所示,则下列结论:(1)ac>0;(2)方程ax2+bx+c=0的两根之积小于0;(3)a+b+c<0;(4)ac+b+1 <0,其中符合题意的个数( )
A.1个 B.2个 C.3个 D.4个
5.下列抛物线中,与x轴有两个交点的是( )
A.y=5x2-7x+5 B.y=16x2-24x+9
C.y=2x2+3x-4 D.y=3x2-2+2
6.若二次函数 (a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1A.a>0 B.b2-4ac≥0
C.x17.汽车在刹车后,由于惯性作用还要继续向前滑行一段距离才能停下,我们称这段距离为“刹车距离”,刹车距离往往跟行驶速度有关,在一个限速35km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不妙,同时刹车,最后还是相撞了事发后,交警现场测得甲车的刹车距离略超过12m,乙车的刹车距离略超过10m,又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)的关系大致如下:S甲 ,S乙 .由此可以推测( )
A.甲车超速 B.乙车超速
C.两车都超速 D.两车都未超速
8.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x
…
﹣1
0
1
3
…
y
…
﹣3
1
3
1
…
则方程ax2+bx+c=0的正根介于( )
A.3与4之间 B.2与3之间
C.1与2之间 D.0与1之间
二、填空(本题共计6小题,每空5分,共计30分)
9.已知方程2x2﹣3x﹣5=0两根为 ,﹣1,则抛物线y=2x2﹣3x﹣5与x轴两个交点间距离为 .
10.抛物线y=ax2+bx+c的对称轴是x=2,其函数图象与x轴有两个交点,其中一个交点的坐标为(5,0),则另一个交点坐标为 .
11.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为 ,两侧距底面 高处各有一盏灯,两灯间的水平距离为 ,则这个隧道入口的最大高度为 .
12.某民房发生火灾.两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F.若点B和点E、点C和点F的离地高度分别相同,现消防员将水流抛物线向上平移5m,再向左后退 m,恰好把水喷到F处进行灭火.
13.设A、B、C三点依次分别是抛物线y=x2﹣4x﹣5与y轴的交点以及与x轴的两个交点,则△ABC的面积是
14. 如图,是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是 .(只要求填写正确命题的序号)
三、解答(本题共计4小题,共50分)
15.(10分)给定关于 的二次函数 ,
学生甲:当 时,抛物线与 轴只有一个交点,因此当抛物线与 轴只有一个交点时, 的值为3;
学生乙:如果抛物线在 轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
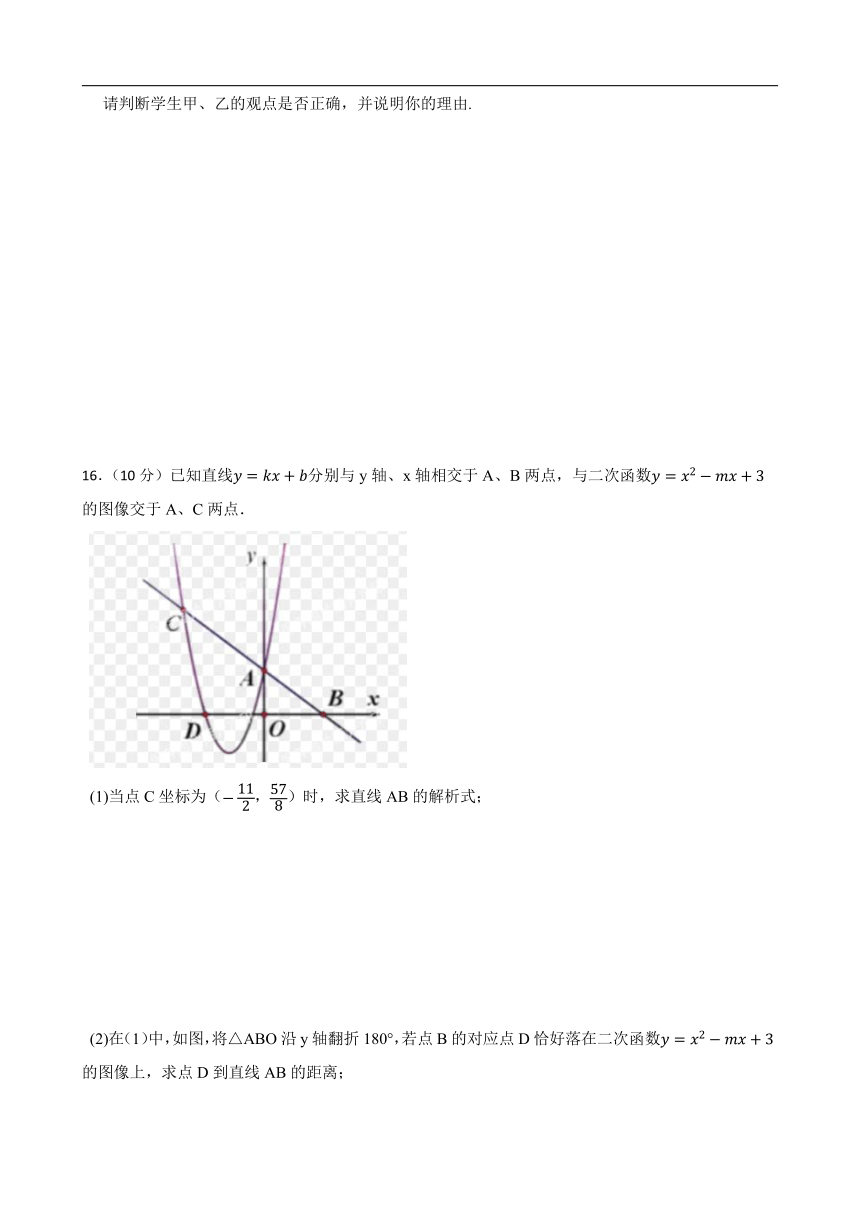
16.(10分)已知直线分别与y轴、x轴相交于A、B两点,与二次函数的图像交于A、C两点.
(1)当点C坐标为(,)时,求直线AB的解析式;
(2)在(1)中,如图,将△ABO沿y轴翻折180°,若点B的对应点D恰好落在二次函数的图像上,求点D到直线AB的距离;
(3)当-1≤x≤1时,二次函数有最小值-3,求实数m的值.
17.(15分)如图所示的是一座拱桥,桥洞的拱形是抛物线的形状,当水面宽AB为12米时,桥洞顶部离水面4米,若水面上涨1米,求此时水面的宽.
18.(15分)已知抛物线C:y=x2+(2m﹣1)x﹣2m.
(1)若m=1,抛物线C交x轴于A,B两点,求AB的长;
(2)若一次函数y=kx+mk的图象与抛物线C有唯一公共点,求m的取值范围;
答案部分
1.D
2.B
3.C
4.C
5.C
6.D
7.B
8.A
9.
10.(﹣1,0)
11.
12.5
13.15
14.①③
15.解:甲的观点是错误的.理由如下:当抛物线 与 轴只有一个交点时 即: 解得 或 即 或 时抛物线 与 轴只有一个交点乙的观点是正确的理由如下:当抛物线在 轴上方时,由上可得 即: ∴而对于开口向上的抛物线最低点为其顶点顶点的横坐标为 ,且抛物线在 轴上方,即抛物线的最低点在第二象限
16.解答(1)∵点C(,)在抛物线上,
∴
解得:m=,
∴
在直线中,令x=0,则y=b,
∴A(0,b)
把A点坐标代入得,b=3
即A(0,3)
把(,),A(0,3)代入,得
,解得:,
所以直线AB的解析式为:.
(2)令y=0,则x=4,故B(4,0)
∴D(-4,0).
连接CD,在△BCD中,BD=8,BC=
过D作DE⊥BC,垂足为E.则.
解得:DE=4.8
(3)∵抛物线的对称轴为,
∴当时,x=-1时二次函数的最小值为-3,得:,
解得:m=-7;
当-1<<1时,x=时二次函数的最小值为-3,得:,
解得:m=或,舍去.
当≥1时,x=1时二次函数的最小值为-3,得:12-m+3=-3,解得:m=7;
所以实数m的值为7或-7.
17.解:如图,以抛物线的顶点为原点,建立平面直角坐标系.
由题意可知抛物线过点(6,-4)
设抛物线的函数表达式为:
把(6,-4)代入 ,可得
则抛物线的函数表达式为:
当水面上涨1米,水面所在的位置为直线
令 ,则 ,解得:
∴此时水面的宽为:6 米.
18.解:(1)m=1时,抛物线为:y=x2+x﹣2,
令y=0得到:x2+x﹣2=0,解得x=﹣2或1,
所以点A(﹣2,0),点B(1,0),
所以AB=3.
(2)由消去y得到:x2+(2m﹣1﹣k)x﹣2m﹣mk=0,
∵一次函数y=kx+mk的图象与抛物线有唯一公共点,
∴△=0,
∴(2m﹣1﹣k)2+8m+4mk=0,
整理得:﹣4m2﹣4m=(k+1)2,
∵(k+1)2≥0,
设y=﹣4m2﹣4m,当y≥0时,﹣1≤m≤0,
∴﹣1≤m≤0时,一次函数y=kx+mk的图象与抛物线C有唯一公共点.
(限时70分钟 满分120分)
一、选择(本题共计8小题,每题5分,共计40分)
1.如图,点 在二次函数 的图象上,则方程 解的一个近似值可能是( )
A.2.18 B.2.68 C.-0.51 D.2.45
2.已知二次函数y=ax2+bx+1,一次函数y=k(x-1)-,若它们的图象对于任意的非零实数k都只有一个公共点,则a,b的值分别为( )
A.a=1,b=2 B.a=1,b=-2 C.a=-1,b=2 D.a=-1,b=-2
3.对于二次函数y=x2﹣4x+7的图象,下列说法正确的是( )
A.开口向下 B.对称轴是x=﹣2
C.顶点坐标是(2,3) D.与x轴有两个交点
4.已知二次函数y=ax2+bx+c( )的图像如图所示,则下列结论:(1)ac>0;(2)方程ax2+bx+c=0的两根之积小于0;(3)a+b+c<0;(4)ac+b+1 <0,其中符合题意的个数( )
A.1个 B.2个 C.3个 D.4个
5.下列抛物线中,与x轴有两个交点的是( )
A.y=5x2-7x+5 B.y=16x2-24x+9
C.y=2x2+3x-4 D.y=3x2-2+2
6.若二次函数 (a≠0)的图象与x轴有两个交点,坐标分别为(x1,0),(x2,0),且x1
C.x1
A.甲车超速 B.乙车超速
C.两车都超速 D.两车都未超速
8.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x
…
﹣1
0
1
3
…
y
…
﹣3
1
3
1
…
则方程ax2+bx+c=0的正根介于( )
A.3与4之间 B.2与3之间
C.1与2之间 D.0与1之间
二、填空(本题共计6小题,每空5分,共计30分)
9.已知方程2x2﹣3x﹣5=0两根为 ,﹣1,则抛物线y=2x2﹣3x﹣5与x轴两个交点间距离为 .
10.抛物线y=ax2+bx+c的对称轴是x=2,其函数图象与x轴有两个交点,其中一个交点的坐标为(5,0),则另一个交点坐标为 .
11.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为 ,两侧距底面 高处各有一盏灯,两灯间的水平距离为 ,则这个隧道入口的最大高度为 .
12.某民房发生火灾.两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F.若点B和点E、点C和点F的离地高度分别相同,现消防员将水流抛物线向上平移5m,再向左后退 m,恰好把水喷到F处进行灭火.
13.设A、B、C三点依次分别是抛物线y=x2﹣4x﹣5与y轴的交点以及与x轴的两个交点,则△ABC的面积是
14. 如图,是二次函数 y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题是 .(只要求填写正确命题的序号)
三、解答(本题共计4小题,共50分)
15.(10分)给定关于 的二次函数 ,
学生甲:当 时,抛物线与 轴只有一个交点,因此当抛物线与 轴只有一个交点时, 的值为3;
学生乙:如果抛物线在 轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
16.(10分)已知直线分别与y轴、x轴相交于A、B两点,与二次函数的图像交于A、C两点.
(1)当点C坐标为(,)时,求直线AB的解析式;
(2)在(1)中,如图,将△ABO沿y轴翻折180°,若点B的对应点D恰好落在二次函数的图像上,求点D到直线AB的距离;
(3)当-1≤x≤1时,二次函数有最小值-3,求实数m的值.
17.(15分)如图所示的是一座拱桥,桥洞的拱形是抛物线的形状,当水面宽AB为12米时,桥洞顶部离水面4米,若水面上涨1米,求此时水面的宽.
18.(15分)已知抛物线C:y=x2+(2m﹣1)x﹣2m.
(1)若m=1,抛物线C交x轴于A,B两点,求AB的长;
(2)若一次函数y=kx+mk的图象与抛物线C有唯一公共点,求m的取值范围;
答案部分
1.D
2.B
3.C
4.C
5.C
6.D
7.B
8.A
9.
10.(﹣1,0)
11.
12.5
13.15
14.①③
15.解:甲的观点是错误的.理由如下:当抛物线 与 轴只有一个交点时 即: 解得 或 即 或 时抛物线 与 轴只有一个交点乙的观点是正确的理由如下:当抛物线在 轴上方时,由上可得 即: ∴而对于开口向上的抛物线最低点为其顶点顶点的横坐标为 ,且抛物线在 轴上方,即抛物线的最低点在第二象限
16.解答(1)∵点C(,)在抛物线上,
∴
解得:m=,
∴
在直线中,令x=0,则y=b,
∴A(0,b)
把A点坐标代入得,b=3
即A(0,3)
把(,),A(0,3)代入,得
,解得:,
所以直线AB的解析式为:.
(2)令y=0,则x=4,故B(4,0)
∴D(-4,0).
连接CD,在△BCD中,BD=8,BC=
过D作DE⊥BC,垂足为E.则.
解得:DE=4.8
(3)∵抛物线的对称轴为,
∴当时,x=-1时二次函数的最小值为-3,得:,
解得:m=-7;
当-1<<1时,x=时二次函数的最小值为-3,得:,
解得:m=或,舍去.
当≥1时,x=1时二次函数的最小值为-3,得:12-m+3=-3,解得:m=7;
所以实数m的值为7或-7.
17.解:如图,以抛物线的顶点为原点,建立平面直角坐标系.
由题意可知抛物线过点(6,-4)
设抛物线的函数表达式为:
把(6,-4)代入 ,可得
则抛物线的函数表达式为:
当水面上涨1米,水面所在的位置为直线
令 ,则 ,解得:
∴此时水面的宽为:6 米.
18.解:(1)m=1时,抛物线为:y=x2+x﹣2,
令y=0得到:x2+x﹣2=0,解得x=﹣2或1,
所以点A(﹣2,0),点B(1,0),
所以AB=3.
(2)由消去y得到:x2+(2m﹣1﹣k)x﹣2m﹣mk=0,
∵一次函数y=kx+mk的图象与抛物线有唯一公共点,
∴△=0,
∴(2m﹣1﹣k)2+8m+4mk=0,
整理得:﹣4m2﹣4m=(k+1)2,
∵(k+1)2≥0,
设y=﹣4m2﹣4m,当y≥0时,﹣1≤m≤0,
∴﹣1≤m≤0时,一次函数y=kx+mk的图象与抛物线C有唯一公共点.
