苏科版八年级数学下册 11.1 反比例函数_(2) 课件(共23张PPT)
文档属性
| 名称 | 苏科版八年级数学下册 11.1 反比例函数_(2) 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 16:44:06 | ||
图片预览





文档简介
(共23张PPT)
学习目标
1、经历抽象反比例函数概念的过程,体会反比例函数的含义,理解反比例函数的概念。
2、理解反比例函数的意义,根据题目条件会求对应量的值,能用待定系数法求反比例函数关系式。
3、在经历实际问题中探索数量关系的过程,养成用数学思维方式解决实际问题的习惯,体会数学在解决实际问题中的作用。
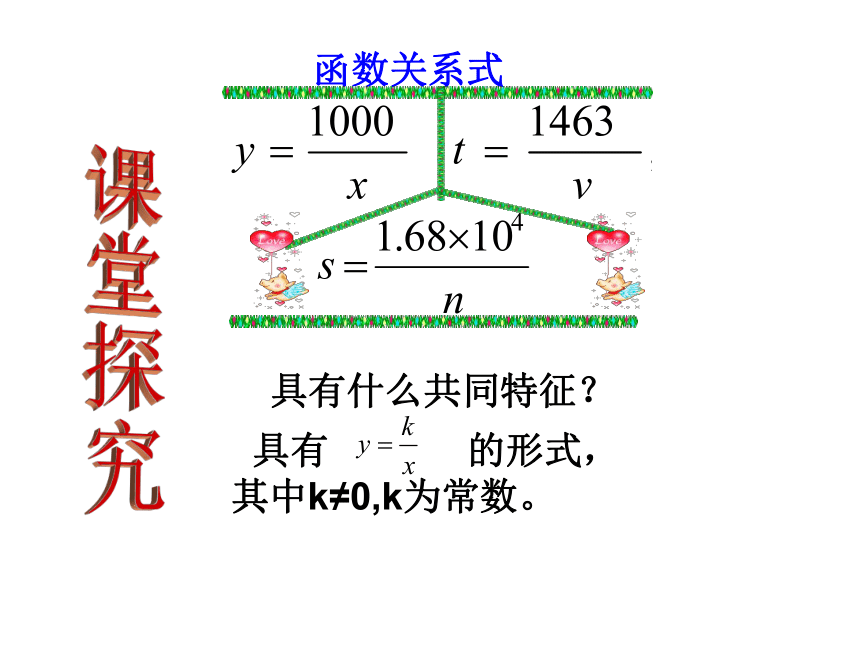
函数关系式
具有什么共同特征?
具有 的形式,其中k≠0,k为常数。
一般地,如果变量 y 和 x 之间函数
关系可以表示成 (k是常数,且k≠ 0)
的形式,则称 y 是 x 的反比例函数。
反比例函数中自变量x的取值范围是什么
n
1.68 ×104
s=
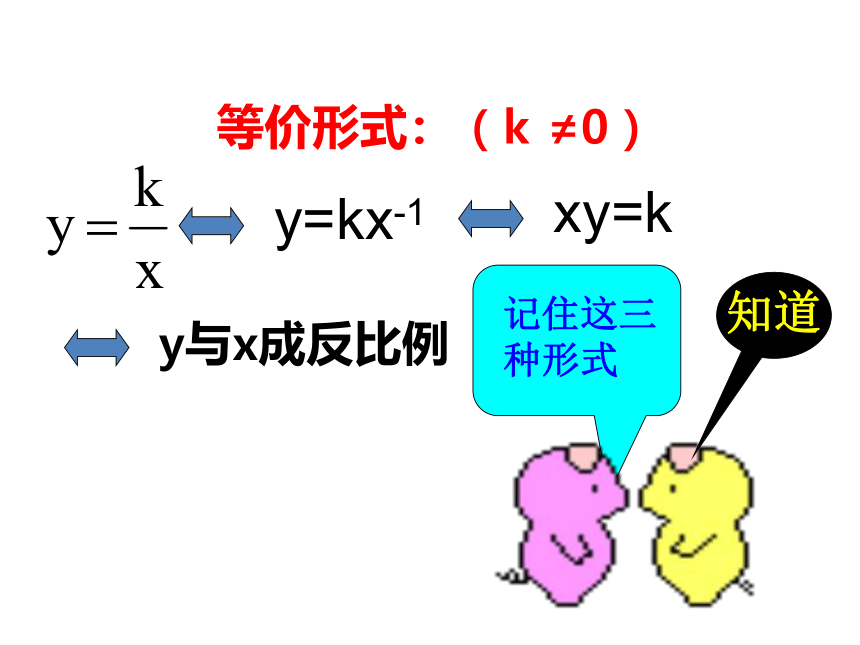
等价形式:(k ≠0)
y=kx-1
xy=k
y与x成反比例
记住这三种形式
知道
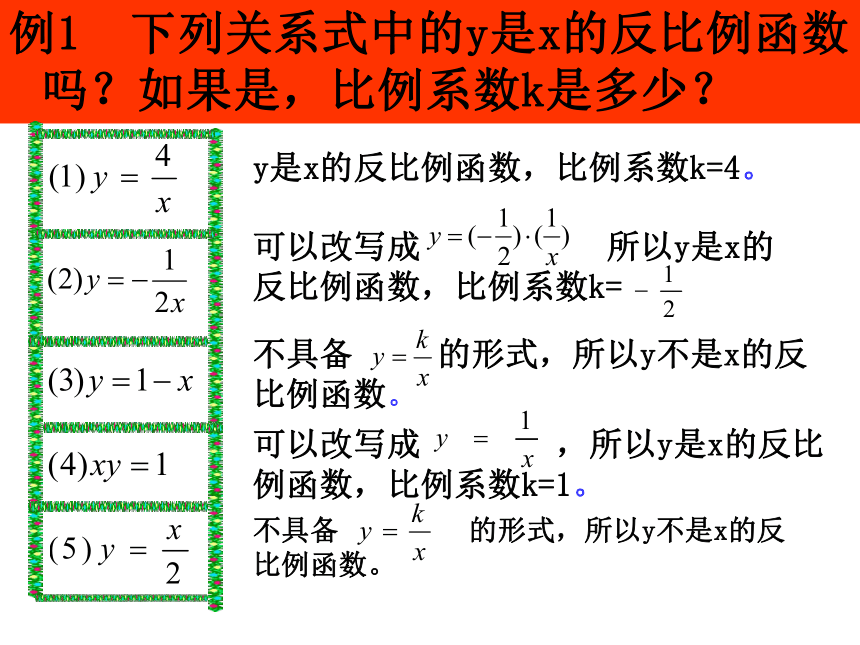
例1 下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
可以改写成 ,所以y是x的反比例函数,比例系数k=1。
不具备 的形式,所以y不是x的反比例函数。
y是x的反比例函数,比例系数k=4。
不具备 的形式,所以y不是x的反比例函数。
可以改写成 所以y是x的
反比例函数,比例系数k=
1、下列关系是反比例函数的是:
(1)圆的周长C与圆的半径R;
(2)圆的面积S与圆的半径R;
(3)汽车从A地到B地所需的时间t与平均速度v;
(4)当电池的电压一定时,电阻R与电流强度I。
请判断:
(√)
(×)
(√)
(×)
1. 在下列函数中,y是x的反比例函数的是( )
(A) (B) + 7
(C)xy = 5 (D)
2.已知函数 是正比例函数,则 m=___ ;
已知函数 是反比例函数,则 m = ___ 。
y =
8
X+5
y =
x
3
y =
x2
2
y = xm -7
y = 3xm -7
C
8
6
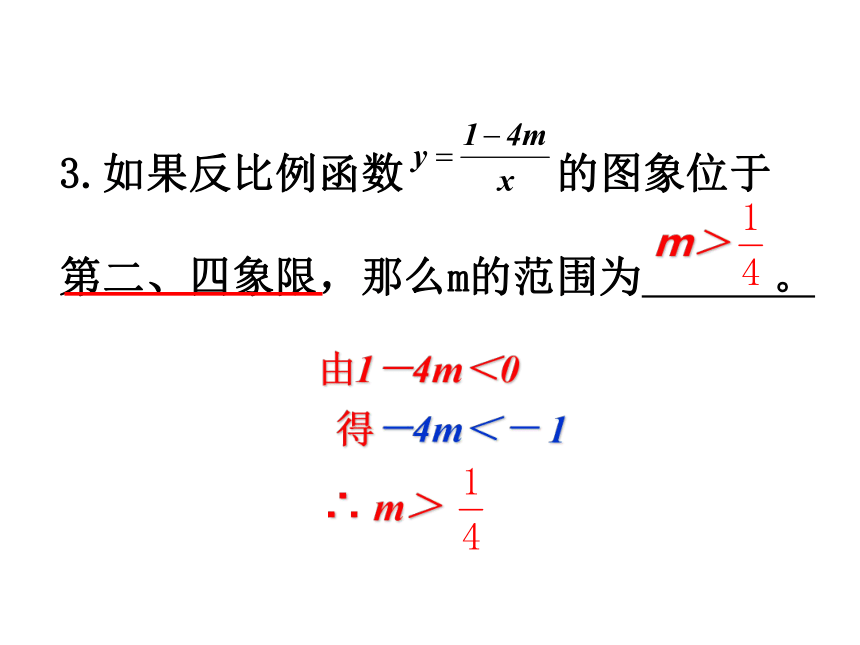
3.如果反比例函数 的图象位于第二、四象限,那么m的范围为 。
由1-4m<0
得-4m<- 1
m>
m>
∴
4.关系式xy+4=0中y是x的反比例函数吗 若是,比例系数k等于多少?若不是,请说明理由。
xy+4=0可以改写成
比例系数k等于-4
所以y是x的反比例函数
1.已知y是x的反比例函数,当x=2时,y=6。
写出y与x的函数关系式:
求当x=4时y的值。
因为当 x=2 时y=6,所以有
∵y与x的函数关系式为
⑵ 把 x=4 代入 得
情寄“待定系数法求函数的解析式
(1).写出这个反比例函数的表达式;
解:∵ y是x的反比例函数,
(2).根据函数表达式完成上表。
2
-4
1
2.y是x的反比例函数,下表给出了x与y的一些值。9
把x= ,y=4代入上式得:
当m= 时,关于x的函数
y=(m+1)xm2-2是反比例函数?
分析:
{
m2-2=-1
m+1≠0
{
即
m=±1
m≠-1
1
A. S1>S2
B.S1C.S1=S2
D.S1与S2的大小关系
不能确定
c
如图,A、C是函数 的图象上的任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记RtΔAOB的面积为S1,RtΔCOD的面积为S2,则( )
S1
S2
1、
反比例函数y= 的图象 如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2, 则k的值为( )
(A)2 (B)-2 (C) -4 (D) 4
N
M
x
y
O
C
2、
如图,在平面直角坐标系中,A为y轴正半轴上一点,过A作x轴的平行线,交函
数 的图象于B,交函数
的图象于C,过C作y轴的平行线交x轴于D。四边形BODC的面积为 。
7
E
3、
4、图中两个三角形的面
积各是___
1
2
5、S⊿ABC的面积=____
2
6、如图所示。如果函数y=-kx(k≠0)与 图像交于A、B两点,过点A作AC垂直于y轴,垂足为点C,则△BOC的面积为 。
S ⊿BOC =S ⊿AOC
S⊿AOC =∣-4 ∣= 2
D
2
o
A
C
x
B
y
D
C
D
o
A
x
B
y
7、四边形ABCD的面积=_____
2
如图,D是反比例函数 的图像上一点,过D作DE⊥x轴于E,DC⊥y轴
于C,一次函数y=-x+2与x轴交
于A点,四边形DEAC的面积
为4,求k的值。
A
E
D
C
O
x
y
F
B
解:当X=0时, y=2. 即 C (0 ,2)
例:
当y=0时, x=2. 即 A (2 ,0)
∴S⊿AOC =2
∴S四边形DCOE =4-2=2
∴K=-2
A
B
C
E
O
F
x
y
x
如图,已知双曲线 (x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=____。
2
S⊿AOF = S矩形AOCB
S⊿AOF = S四边形EOBF =1
例:
解:(1)设函数关系式为y=k/(x-0.4),又当x=0.65元时,y=0.8,则 有 0.8=k/(0.65-0.4),解得k=0.2.
∴y与x之间的函数关系式为y=0.2/(x-0.4),即 。
某地上年度电价为0.8元,年用电量为1亿度,本年度计划将电价调至0.55~0.75元之间,经测算,若电价调至x元,则本年度新增用电量y(亿度)与(x-0.4)元成反比例.又当x=0.65元时,y=0.8.(1)求y与x之间的函数关系式;(2)若每度电的成本价0.3元,电价调至0.6元,请你预算一下本年度电力部门的纯收人多少
(2)把x=0.6代入y=0.2/(x-0.4),得y=1.即本年度新增用电量1亿度
则本年度总用电量为(1+1=2)亿度
∴本年度电力部门的纯收入为:2×(0.6-0.3)=0.6亿元。
学习目标
1、经历抽象反比例函数概念的过程,体会反比例函数的含义,理解反比例函数的概念。
2、理解反比例函数的意义,根据题目条件会求对应量的值,能用待定系数法求反比例函数关系式。
3、在经历实际问题中探索数量关系的过程,养成用数学思维方式解决实际问题的习惯,体会数学在解决实际问题中的作用。
函数关系式
具有什么共同特征?
具有 的形式,其中k≠0,k为常数。
一般地,如果变量 y 和 x 之间函数
关系可以表示成 (k是常数,且k≠ 0)
的形式,则称 y 是 x 的反比例函数。
反比例函数中自变量x的取值范围是什么
n
1.68 ×104
s=
等价形式:(k ≠0)
y=kx-1
xy=k
y与x成反比例
记住这三种形式
知道
例1 下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?
可以改写成 ,所以y是x的反比例函数,比例系数k=1。
不具备 的形式,所以y不是x的反比例函数。
y是x的反比例函数,比例系数k=4。
不具备 的形式,所以y不是x的反比例函数。
可以改写成 所以y是x的
反比例函数,比例系数k=
1、下列关系是反比例函数的是:
(1)圆的周长C与圆的半径R;
(2)圆的面积S与圆的半径R;
(3)汽车从A地到B地所需的时间t与平均速度v;
(4)当电池的电压一定时,电阻R与电流强度I。
请判断:
(√)
(×)
(√)
(×)
1. 在下列函数中,y是x的反比例函数的是( )
(A) (B) + 7
(C)xy = 5 (D)
2.已知函数 是正比例函数,则 m=___ ;
已知函数 是反比例函数,则 m = ___ 。
y =
8
X+5
y =
x
3
y =
x2
2
y = xm -7
y = 3xm -7
C
8
6
3.如果反比例函数 的图象位于第二、四象限,那么m的范围为 。
由1-4m<0
得-4m<- 1
m>
m>
∴
4.关系式xy+4=0中y是x的反比例函数吗 若是,比例系数k等于多少?若不是,请说明理由。
xy+4=0可以改写成
比例系数k等于-4
所以y是x的反比例函数
1.已知y是x的反比例函数,当x=2时,y=6。
写出y与x的函数关系式:
求当x=4时y的值。
因为当 x=2 时y=6,所以有
∵y与x的函数关系式为
⑵ 把 x=4 代入 得
情寄“待定系数法求函数的解析式
(1).写出这个反比例函数的表达式;
解:∵ y是x的反比例函数,
(2).根据函数表达式完成上表。
2
-4
1
2.y是x的反比例函数,下表给出了x与y的一些值。9
把x= ,y=4代入上式得:
当m= 时,关于x的函数
y=(m+1)xm2-2是反比例函数?
分析:
{
m2-2=-1
m+1≠0
{
即
m=±1
m≠-1
1
A. S1>S2
B.S1
D.S1与S2的大小关系
不能确定
c
如图,A、C是函数 的图象上的任意两点,过A作x轴的垂线,垂足为B,过C作y轴的垂线,垂足为D,记RtΔAOB的面积为S1,RtΔCOD的面积为S2,则( )
S1
S2
1、
反比例函数y= 的图象 如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2, 则k的值为( )
(A)2 (B)-2 (C) -4 (D) 4
N
M
x
y
O
C
2、
如图,在平面直角坐标系中,A为y轴正半轴上一点,过A作x轴的平行线,交函
数 的图象于B,交函数
的图象于C,过C作y轴的平行线交x轴于D。四边形BODC的面积为 。
7
E
3、
4、图中两个三角形的面
积各是___
1
2
5、S⊿ABC的面积=____
2
6、如图所示。如果函数y=-kx(k≠0)与 图像交于A、B两点,过点A作AC垂直于y轴,垂足为点C,则△BOC的面积为 。
S ⊿BOC =S ⊿AOC
S⊿AOC =∣-4 ∣= 2
D
2
o
A
C
x
B
y
D
C
D
o
A
x
B
y
7、四边形ABCD的面积=_____
2
如图,D是反比例函数 的图像上一点,过D作DE⊥x轴于E,DC⊥y轴
于C,一次函数y=-x+2与x轴交
于A点,四边形DEAC的面积
为4,求k的值。
A
E
D
C
O
x
y
F
B
解:当X=0时, y=2. 即 C (0 ,2)
例:
当y=0时, x=2. 即 A (2 ,0)
∴S⊿AOC =2
∴S四边形DCOE =4-2=2
∴K=-2
A
B
C
E
O
F
x
y
x
如图,已知双曲线 (x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为2,则k=____。
2
S⊿AOF = S矩形AOCB
S⊿AOF = S四边形EOBF =1
例:
解:(1)设函数关系式为y=k/(x-0.4),又当x=0.65元时,y=0.8,则 有 0.8=k/(0.65-0.4),解得k=0.2.
∴y与x之间的函数关系式为y=0.2/(x-0.4),即 。
某地上年度电价为0.8元,年用电量为1亿度,本年度计划将电价调至0.55~0.75元之间,经测算,若电价调至x元,则本年度新增用电量y(亿度)与(x-0.4)元成反比例.又当x=0.65元时,y=0.8.(1)求y与x之间的函数关系式;(2)若每度电的成本价0.3元,电价调至0.6元,请你预算一下本年度电力部门的纯收人多少
(2)把x=0.6代入y=0.2/(x-0.4),得y=1.即本年度新增用电量1亿度
则本年度总用电量为(1+1=2)亿度
∴本年度电力部门的纯收入为:2×(0.6-0.3)=0.6亿元。
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
