10.2一次函数与它的图像 同步练习(含解析)
文档属性
| 名称 | 10.2一次函数与它的图像 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 134.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 11:54:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
10.2一次函数与它的图像同步练习青岛版初中数学八年级下册
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共10小题,共30分)
在平面直角坐标系中,函数的图象如图所示,则下列判断正确的是
A. B.
C. D.
如图,一次函数的图象分别与轴、轴的负半轴相交于、,则下列结论一定正确的是
A.
B.
C.
D.
若函数是正比例函数,则和的值为
A. , B. ,
C. , D. ,
已知是正比例函数,则的值是
A. B. C. D.
下列函数关系式:;;;;其中是一次函数的是
A. B. C. D.
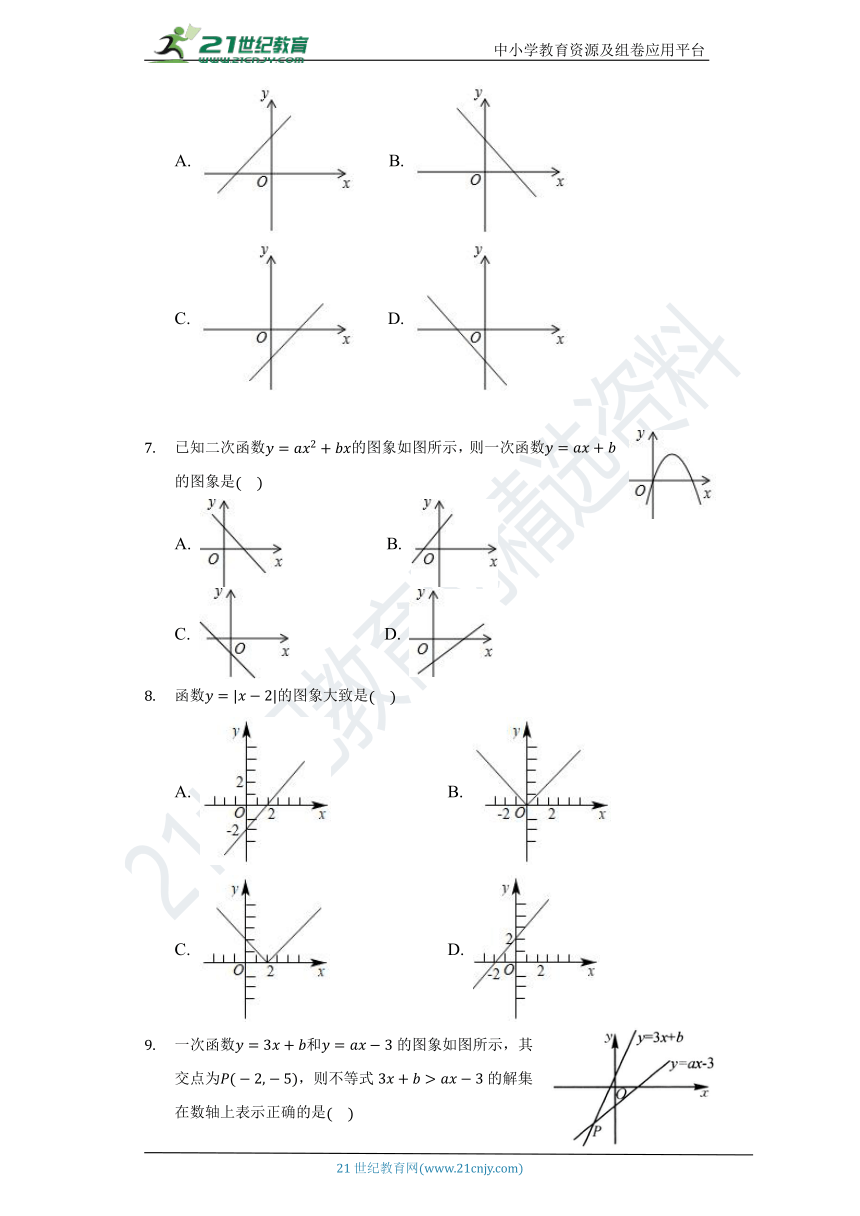
二次函数的图象如图所示,则一次函数的图象大致是
A. B.
C. D.
已知二次函数的图象如图所示,则一次函数的图象是
A. B.
C. D.
函数的图象大致是
A. B.
C. D.
一次函数和的图象如图所示,其交点为,则不等式的解集在数轴上表示正确的是
A. B.
C. D.
有下列五个式子:;;;;其中是的一次函数的有
A. 个 B. 个 C. 个 D. 个
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
若是关于的正比例函数,则的值为______.
当________时,函数是关于的正比例函数.
若函数是关于的一次函数,那么的取值范围是______.
已知函数是正比例函数,则的值是____.
三、解答题(本大题共5小题,共40分)
甲、乙两人要去同一个地方玩,甲上午点出发,一个小时后乙出发,下图反映的是两人从出发到目的地的路程与时间之间的关系,根据关系图回答下面问题:
乙到达终点用了多少时间?
从点到点,甲在做什么?
在这个过程中乙总共走了多少千米?他的平均速度是多少?
从点到点,两人谁的速度快?快多少?
甲出发以后,两人有几次相遇?分别在什么时间?
已知函数.
当为何值时,是的一次函数?
当为何值时,是的正比例函数?
在同一直角坐标系中画出和的图像.
已知与成正比例,且当时.
求与之间的函数解析式.
求时,的值.
求为何值时,.
在同一直角坐标系中,画出函数,,,的图像,并找出每两个函数图像之间的共同特征.
答案和解析
1.【答案】
【解析】解:一次函数的图象经过一、二、四象限,
,.
,
故选:.
根据一次函数的图象与系数的关系进行解答即可.
本题考查的是一次函数的图象与系数的关系,即一次函数中,当,时图象在一、二、四象限.
2.【答案】
【解析】解:一次函数的图象经过第二、三、四象限,
,,
.
故选D.
由一次函数图象经过第二、三、四象限,即可得出、,继而可得出,此题得解.
本题考查了一次函数图象与系数的关系,牢记“,的图象在二、三、四象限”是解题的关键.
3.【答案】
【解析】解:由题意得:,,且,
解得:,,
故选:.
根据正比例函数定义可得,,且,再解即可.
此题主要考查了正比例函数定义,关键是掌握形如是常数,的函数叫做正比例函数.
4.【答案】
【解析】解:是正比例函数,
且,
解得.
故选:.
直接利用正比例函数的定义分析得出即可.
此题主要考查了正比例函数的定义,解题关键是掌握正比例函数的定义条件:正比例函数的定义条件是:为常数且,自变量次数为.
5.【答案】
【解析】解:是一次函数;
自变量在分母,故不是一次函数;
自变量次数不为,故不是一次函数;
是常数,不含自变量,故不是一次函数;
是一次函数.
所以一次函数是.
故选:.
根据一次函数的定义条件进行逐一分析即可.
本题主要考查了一次函数的定义,一次函数的定义条件是:、为常数,,自变量次数为.
6.【答案】
【解析】解:由二次函数图象,得出,,,
A、一次函数图象,得,,故A错误;
B、一次函数图象,得,,故B错误;
C、一次函数图象,得,,故C错误;
D、一次函数图象,得,,故D正确;
故选:.
可先根据二次函数的图象判断、的符号,再判断一次函数图象与实际是否相符,判断正误.
本题考查了二次函数图象,应该熟记一次函数在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.
7.【答案】
【解析】解:如图所示:抛物线开口向下,则,则,互为相反数,
则,
故一次函数的图象经过第一、二、四象限.
故选:.
直接利用二次函数图象得出,的符号,进而利用一次函数的图象性质得出答案.
此题主要考查了二次函数以及一次函数的图象,正确得出,的符号是解题关键.
8.【答案】
【解析】解:.
选项A、D错误.
又函数图象经过点,
选项B错误,选项C正确.
故选:.
由绝对值的性质知,该图象的函数值,且函数图象经过点,由此得到正确的函数图象.
考查了一次函数的图象,解题时,需要掌握函数的图象的特殊点.
9.【答案】
【解析】略
10.【答案】
【解析】
【分析】
本题主要考查了一次函数的定义,一次函数的定义条件是:、为常数,,自变量次数为.
根据一次函数的定义条件进行逐一分析即可.
【解答】
解:变形为,自变量的指数不是,故不是一次函数;
变形为,是一次函数;
变形为,自变量在分母上,不是一次函数;
变形为,自变量在分母上,不是一次函数;
自变量的指数不是,不是一次函数;
故选A.
11.【答案】
【解析】解:是关于的正比例函数,
,,
解得:.
故答案为:.
直接利用正比例函数的定义进而得出答案.
此题主要考查了正比例函数的定义,正确把握定义是解题关键.
12.【答案】
【解析】
【分析】
本题主要考查了正比例函数的定义,正比例函数的一般形式为:,解答此题根据正比例函数的定义可得关于的方程和不等式,然后解之即可.
【解答】
解:函数是正比例函数,
解得:,
当时,函数是关于的正比例函数.
故答案为.
13.【答案】
【解析】解:是关于的一次函数,
,则,
故答案为:.
根据一次函数的定义得到:,由此求得的取值范围.
本题考查一次函数的定义,属于基础题,注意掌握一次函数的定义条件是:、为常数,,自变量的次数为.
14.【答案】
【解析】
【分析】
此题主要考查了正比例函数的定义,正确把握定义是解题关键.
直接利用正比例函数的定义分析得出答案.
【解答】
解:函数是正比例函数,
,,解得:.
故答案为.
15.【答案】解:根据图象即可得出乙到达终点用了小时;
从点到点,甲在休息或修车;
在这个过程中乙总共走了千米;他的平均速度是;
从点到点,甲的速度为:;乙的速度为:,故甲的速度快,比乙快千米小时.
乙在时到时的速度为,
,
甲出发以后,两人有两次相遇,分别在时分和时.
【解析】本题考查一次函数的图像,解题的关键是明确图像含义,找出所求问题需要的条件.
根据函数图象便可得出乙到达终点用了小时;
由图象可知,时间在增多,路程没有变化,表现在函数图象上是与轴平行的线段,便可得出甲在休息或修车;
从图中便可得出结果;
从图中可以得出点到点甲的速度,乙的速度,比较即可得出结果;
从图中可以得出两次相遇,分别在时分和时.
16.【答案】解:由题意得:,
解得:;
由题意得:,且,
解得:.
【解析】利用一次函数定义进行解答即可;
利用正比例函数定义进行解答.
此题主要考查了正比例函数定义和一次函数定义,关键是掌握形如是常数,的函数叫做正比例函数.
17.【答案】解:函数与在同一直角坐标系中的图像如图所示.
【解析】见答案
18.【答案】解: .
【解析】略
19.【答案】解:图像如图所示.
平行,平行,
关于轴对称且相互垂直,
关于轴对称且相互垂直,
关于轴对称且相互垂直,
关于轴对称且相互垂直.
四条直线围成一个正方形.
【解析】见答案
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
10.2一次函数与它的图像同步练习青岛版初中数学八年级下册
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共10小题,共30分)
在平面直角坐标系中,函数的图象如图所示,则下列判断正确的是
A. B.
C. D.
如图,一次函数的图象分别与轴、轴的负半轴相交于、,则下列结论一定正确的是
A.
B.
C.
D.
若函数是正比例函数,则和的值为
A. , B. ,
C. , D. ,
已知是正比例函数,则的值是
A. B. C. D.
下列函数关系式:;;;;其中是一次函数的是
A. B. C. D.
二次函数的图象如图所示,则一次函数的图象大致是
A. B.
C. D.
已知二次函数的图象如图所示,则一次函数的图象是
A. B.
C. D.
函数的图象大致是
A. B.
C. D.
一次函数和的图象如图所示,其交点为,则不等式的解集在数轴上表示正确的是
A. B.
C. D.
有下列五个式子:;;;;其中是的一次函数的有
A. 个 B. 个 C. 个 D. 个
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
若是关于的正比例函数,则的值为______.
当________时,函数是关于的正比例函数.
若函数是关于的一次函数,那么的取值范围是______.
已知函数是正比例函数,则的值是____.
三、解答题(本大题共5小题,共40分)
甲、乙两人要去同一个地方玩,甲上午点出发,一个小时后乙出发,下图反映的是两人从出发到目的地的路程与时间之间的关系,根据关系图回答下面问题:
乙到达终点用了多少时间?
从点到点,甲在做什么?
在这个过程中乙总共走了多少千米?他的平均速度是多少?
从点到点,两人谁的速度快?快多少?
甲出发以后,两人有几次相遇?分别在什么时间?
已知函数.
当为何值时,是的一次函数?
当为何值时,是的正比例函数?
在同一直角坐标系中画出和的图像.
已知与成正比例,且当时.
求与之间的函数解析式.
求时,的值.
求为何值时,.
在同一直角坐标系中,画出函数,,,的图像,并找出每两个函数图像之间的共同特征.
答案和解析
1.【答案】
【解析】解:一次函数的图象经过一、二、四象限,
,.
,
故选:.
根据一次函数的图象与系数的关系进行解答即可.
本题考查的是一次函数的图象与系数的关系,即一次函数中,当,时图象在一、二、四象限.
2.【答案】
【解析】解:一次函数的图象经过第二、三、四象限,
,,
.
故选D.
由一次函数图象经过第二、三、四象限,即可得出、,继而可得出,此题得解.
本题考查了一次函数图象与系数的关系,牢记“,的图象在二、三、四象限”是解题的关键.
3.【答案】
【解析】解:由题意得:,,且,
解得:,,
故选:.
根据正比例函数定义可得,,且,再解即可.
此题主要考查了正比例函数定义,关键是掌握形如是常数,的函数叫做正比例函数.
4.【答案】
【解析】解:是正比例函数,
且,
解得.
故选:.
直接利用正比例函数的定义分析得出即可.
此题主要考查了正比例函数的定义,解题关键是掌握正比例函数的定义条件:正比例函数的定义条件是:为常数且,自变量次数为.
5.【答案】
【解析】解:是一次函数;
自变量在分母,故不是一次函数;
自变量次数不为,故不是一次函数;
是常数,不含自变量,故不是一次函数;
是一次函数.
所以一次函数是.
故选:.
根据一次函数的定义条件进行逐一分析即可.
本题主要考查了一次函数的定义,一次函数的定义条件是:、为常数,,自变量次数为.
6.【答案】
【解析】解:由二次函数图象,得出,,,
A、一次函数图象,得,,故A错误;
B、一次函数图象,得,,故B错误;
C、一次函数图象,得,,故C错误;
D、一次函数图象,得,,故D正确;
故选:.
可先根据二次函数的图象判断、的符号,再判断一次函数图象与实际是否相符,判断正误.
本题考查了二次函数图象,应该熟记一次函数在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.
7.【答案】
【解析】解:如图所示:抛物线开口向下,则,则,互为相反数,
则,
故一次函数的图象经过第一、二、四象限.
故选:.
直接利用二次函数图象得出,的符号,进而利用一次函数的图象性质得出答案.
此题主要考查了二次函数以及一次函数的图象,正确得出,的符号是解题关键.
8.【答案】
【解析】解:.
选项A、D错误.
又函数图象经过点,
选项B错误,选项C正确.
故选:.
由绝对值的性质知,该图象的函数值,且函数图象经过点,由此得到正确的函数图象.
考查了一次函数的图象,解题时,需要掌握函数的图象的特殊点.
9.【答案】
【解析】略
10.【答案】
【解析】
【分析】
本题主要考查了一次函数的定义,一次函数的定义条件是:、为常数,,自变量次数为.
根据一次函数的定义条件进行逐一分析即可.
【解答】
解:变形为,自变量的指数不是,故不是一次函数;
变形为,是一次函数;
变形为,自变量在分母上,不是一次函数;
变形为,自变量在分母上,不是一次函数;
自变量的指数不是,不是一次函数;
故选A.
11.【答案】
【解析】解:是关于的正比例函数,
,,
解得:.
故答案为:.
直接利用正比例函数的定义进而得出答案.
此题主要考查了正比例函数的定义,正确把握定义是解题关键.
12.【答案】
【解析】
【分析】
本题主要考查了正比例函数的定义,正比例函数的一般形式为:,解答此题根据正比例函数的定义可得关于的方程和不等式,然后解之即可.
【解答】
解:函数是正比例函数,
解得:,
当时,函数是关于的正比例函数.
故答案为.
13.【答案】
【解析】解:是关于的一次函数,
,则,
故答案为:.
根据一次函数的定义得到:,由此求得的取值范围.
本题考查一次函数的定义,属于基础题,注意掌握一次函数的定义条件是:、为常数,,自变量的次数为.
14.【答案】
【解析】
【分析】
此题主要考查了正比例函数的定义,正确把握定义是解题关键.
直接利用正比例函数的定义分析得出答案.
【解答】
解:函数是正比例函数,
,,解得:.
故答案为.
15.【答案】解:根据图象即可得出乙到达终点用了小时;
从点到点,甲在休息或修车;
在这个过程中乙总共走了千米;他的平均速度是;
从点到点,甲的速度为:;乙的速度为:,故甲的速度快,比乙快千米小时.
乙在时到时的速度为,
,
甲出发以后,两人有两次相遇,分别在时分和时.
【解析】本题考查一次函数的图像,解题的关键是明确图像含义,找出所求问题需要的条件.
根据函数图象便可得出乙到达终点用了小时;
由图象可知,时间在增多,路程没有变化,表现在函数图象上是与轴平行的线段,便可得出甲在休息或修车;
从图中便可得出结果;
从图中可以得出点到点甲的速度,乙的速度,比较即可得出结果;
从图中可以得出两次相遇,分别在时分和时.
16.【答案】解:由题意得:,
解得:;
由题意得:,且,
解得:.
【解析】利用一次函数定义进行解答即可;
利用正比例函数定义进行解答.
此题主要考查了正比例函数定义和一次函数定义,关键是掌握形如是常数,的函数叫做正比例函数.
17.【答案】解:函数与在同一直角坐标系中的图像如图所示.
【解析】见答案
18.【答案】解: .
【解析】略
19.【答案】解:图像如图所示.
平行,平行,
关于轴对称且相互垂直,
关于轴对称且相互垂直,
关于轴对称且相互垂直,
关于轴对称且相互垂直.
四条直线围成一个正方形.
【解析】见答案
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
