3.1.2随机事件的概率(27张)
图片预览







文档简介
课件27张PPT。20.随机事件的概率复习回顾
1.现象的分类
⑴确定性现象
⑵随机现象
2.试验与事件
⑴定义
⑵随机试验的特点
3.事件的分类与表示
⑴不可能事件
⑵必然事件
⑶随机事件事件的分类说明:三种事件都是在“一定条件下”发生的,当条件改变时,事件的类型也可以发生变化。 注:随机试验的特点
⑴可重复性;
⑵所有可能的结果都是预先明确的;
⑶各次试验的结果不一定相同,每次试验前不能预知哪一个结果会发生;
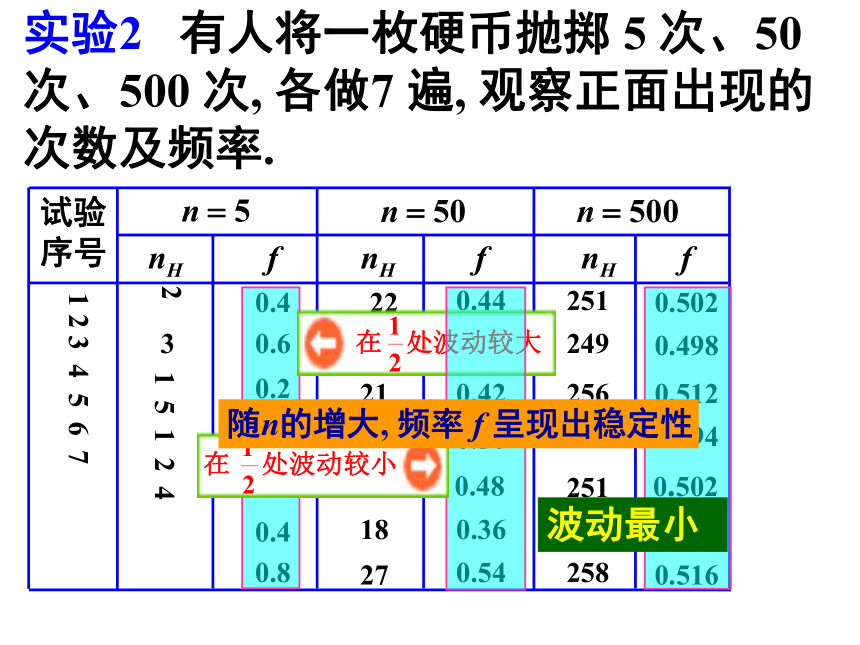
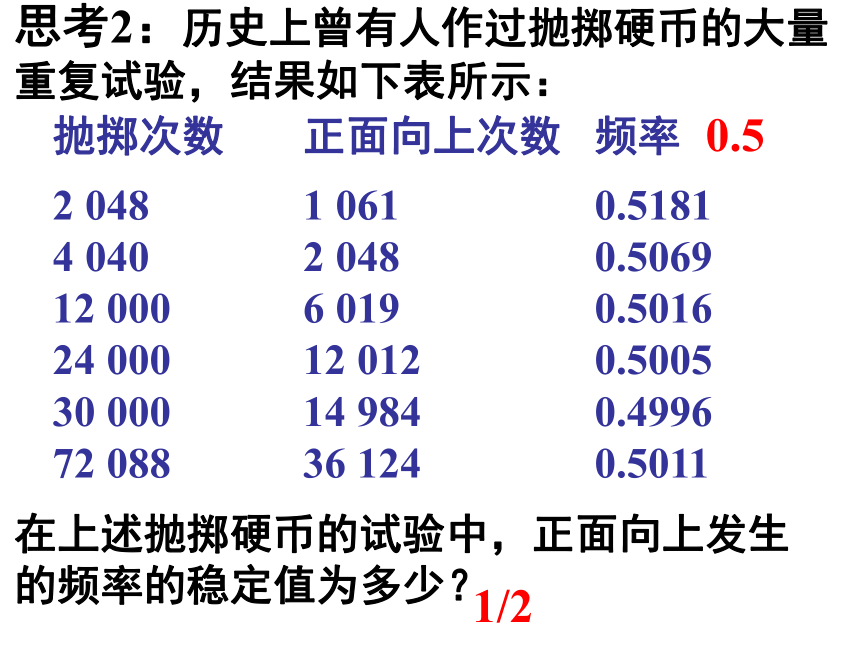
⑷规律性. 物体的大小常用质量、体积等来度量,学习水平的高低常用考试分数来衡量.对于随机事件,它发生的可能性有多大,我们也希望用一个数量来反映. 随机事件的“可能发生也可能不发生”是不是没有任何规律地随意发生呢?一、问题情境思考1:在相同的条件下重复n次试验,若某一事件A出现的次数为m,则称m为事件A出现的频数,那么事件A出现的频率fn(A)等于什么?频率的取值范围是什么? 实验2 有人将一枚硬币抛掷 5 次、50 次、500 次, 各做7 遍, 观察正面出现的次数及频率.波动最小随n的增大, 频率 f 呈现出稳定性思考2:历史上曾有人作过抛掷硬币的大量重复试验,结果如下表所示:
在上述抛掷硬币的试验中,正面向上发生的频率的稳定值为多少?0.51/2思考3:上述试验表明,随机事件A在每次试验中是否发生是不能预知的,但是在大量重复试验后,随着试验次数的增加,事件A发生的频率呈现出一定的规律性,这个规律性是如何体现出来的? 事件A发生的频率较稳定,在某个常数附近摆动. 思考4:既然随机事件A在大量重复试验中发生的频率fn(A)趋于稳定,在某个常数附近摆动,那我们就可以用这个常数来度量事件A发生的可能性的大小,并把这个常数叫做事件A发生的概率,记作P(A).数学建构1、概率的定义 一般地,对于给定的随机事件A,在相同的条件下,随着试验的次数的增加,事件A发生的频率会在某个常数附近摆动并趋于稳定,我们可以用这个常数来刻画随机事件A发生的可能性大小,并把这个常数称为随机事件A的概率,记为P(A)思考5:在实际问题中,随机事件A发生的概率往往是未知的(如在一定条件下射击命中目标的概率),你如何得到事件A发生的概率? 通过大量重复试验得到事件A发生的频率的稳定值,即概率. 思考6:在相同条件下,事件A在先后两次试验中发生的频率fn(A)是否一定相等?事件A在先后两次试验中发生的概率P(A)是否一定相等? 频率具有随机性,做同样次数的重复试验,事件A发生的频率可能不相同;概率是一个确定的数,是客观存在的,与每次试验无关.2、频率与概率的关系(1)区别:频率是重复实验中A发生后的统计结果,对于一个随机事件其发生频率不是固定不变的它会随着试验次数的变化而变化;而概率是事件A的本质属性,事件A的概率是一个常数,它不随着试验的次数改变而变化。(2)联系:当实验次数越大时,频率越向概率靠近,只要实验次数足够大,所得的频率可近似地当作事件A的概率。 注:随机事件的概率是频率的稳定值;频率是概率的近似值。3、求事件的概率的基本方法思考7:必然事件、不可能事件发生的概率分别为多少?概率的取值范围是什么? 4、概率的取值范围 统计事件A在n次实验中发生了m次,则P(A)=m/n 由于0≤m≤n,所以0≤m/n≤1,即0≤P(A)≤1注:(1)必然事件的概率:P(Ω)=1
(2)不可能事件的概率:P(Φ)=0
反之,也成立!三、数学应用例1.下面表中列出10次抛掷硬币的试验结果,n为每次试验抛掷硬币的次数, m为硬币正面向上的次数, 计算每次试验中“正面向上”这一事件的频率, 并考查其概率. 例2.某市统计近几年新生儿出生数及其中男婴数(单位:人)如下:(1)试计算男婴各年出生的频率(精确到0.001);
(2)该市男婴出生的概率是多少?三、数学应用解(1)1999年男婴出生的频率为:例3.在一场足球比赛中,A队获得了一次点球机会, 现A队有2名球负甲,乙想去主罚这次点球,已知这2名队负在此前的点球训练中的成绩如下表:乙:如课你是A队的主教练, 你认为安排甲和乙中的哪个队员去罚这个点球, 罚中的可能性会大些?甲:1.某篮球运动员在同一条件下进行投篮练习,结果如下表:计算表中进球的频率;
这位运动员投篮一次,进球的概率约是多少?(3)这位运动员进球的概率是0.8,那么他投10次篮一定能 投中8次吗?不一定. 投10次篮相当于做10次试验,每次试验的结果都是随机的, 所以投10次篮的结果也是随机的. 概率约是0.80.780.750.800.80 0.85 0.830.80四、学生活动四、学生活动 2、每道选择题有4个选择支,其中只有一个选择支是正确的。某次考试共有12道选择题,某人说:“每个选择支正确的概率是1/4,我每题都选择第一个选择支,则一定有3道题的选择结果正确。”这句话对吗?解:不对四、学生活动 3、掷一枚硬币,连续出现5次正面向上。张欣认为下次出现反面向上的概率大于1/2,你同意吗?为什么?解:不同意,随机事件的发生的概率与该事件以前是否发生无关,故下次发生的概率仍为1/2。四、学生活动4、某医院治疗一种疾病的治愈率为10%,那么,若前9个病人都没有治愈,第10个人就一定能治吗?解:如果把治疗一个病人作为一次试验,治愈率是10%,指随着试验次数的增加,即治疗病人数的增加,大约有10%的人能够治愈,对于一次试验来说,其结果是随机的,因此前9个人没治愈是可能的,对于第10个人来说,其结果仍然是随机的,即有可能治愈的,也可能没有治愈。五、课堂小结(一)知识1、频率、概率的定义及之间的联系2、随机事件的概率的求法
3、事件概率的取值范围(二)题型与方法1、求事件的概率:P(A)≈m/n2、概率的概念的巩固:定义法注意范围:0≤P(A)≤1
1.现象的分类
⑴确定性现象
⑵随机现象
2.试验与事件
⑴定义
⑵随机试验的特点
3.事件的分类与表示
⑴不可能事件
⑵必然事件
⑶随机事件事件的分类说明:三种事件都是在“一定条件下”发生的,当条件改变时,事件的类型也可以发生变化。 注:随机试验的特点
⑴可重复性;
⑵所有可能的结果都是预先明确的;
⑶各次试验的结果不一定相同,每次试验前不能预知哪一个结果会发生;
⑷规律性. 物体的大小常用质量、体积等来度量,学习水平的高低常用考试分数来衡量.对于随机事件,它发生的可能性有多大,我们也希望用一个数量来反映. 随机事件的“可能发生也可能不发生”是不是没有任何规律地随意发生呢?一、问题情境思考1:在相同的条件下重复n次试验,若某一事件A出现的次数为m,则称m为事件A出现的频数,那么事件A出现的频率fn(A)等于什么?频率的取值范围是什么? 实验2 有人将一枚硬币抛掷 5 次、50 次、500 次, 各做7 遍, 观察正面出现的次数及频率.波动最小随n的增大, 频率 f 呈现出稳定性思考2:历史上曾有人作过抛掷硬币的大量重复试验,结果如下表所示:
在上述抛掷硬币的试验中,正面向上发生的频率的稳定值为多少?0.51/2思考3:上述试验表明,随机事件A在每次试验中是否发生是不能预知的,但是在大量重复试验后,随着试验次数的增加,事件A发生的频率呈现出一定的规律性,这个规律性是如何体现出来的? 事件A发生的频率较稳定,在某个常数附近摆动. 思考4:既然随机事件A在大量重复试验中发生的频率fn(A)趋于稳定,在某个常数附近摆动,那我们就可以用这个常数来度量事件A发生的可能性的大小,并把这个常数叫做事件A发生的概率,记作P(A).数学建构1、概率的定义 一般地,对于给定的随机事件A,在相同的条件下,随着试验的次数的增加,事件A发生的频率会在某个常数附近摆动并趋于稳定,我们可以用这个常数来刻画随机事件A发生的可能性大小,并把这个常数称为随机事件A的概率,记为P(A)思考5:在实际问题中,随机事件A发生的概率往往是未知的(如在一定条件下射击命中目标的概率),你如何得到事件A发生的概率? 通过大量重复试验得到事件A发生的频率的稳定值,即概率. 思考6:在相同条件下,事件A在先后两次试验中发生的频率fn(A)是否一定相等?事件A在先后两次试验中发生的概率P(A)是否一定相等? 频率具有随机性,做同样次数的重复试验,事件A发生的频率可能不相同;概率是一个确定的数,是客观存在的,与每次试验无关.2、频率与概率的关系(1)区别:频率是重复实验中A发生后的统计结果,对于一个随机事件其发生频率不是固定不变的它会随着试验次数的变化而变化;而概率是事件A的本质属性,事件A的概率是一个常数,它不随着试验的次数改变而变化。(2)联系:当实验次数越大时,频率越向概率靠近,只要实验次数足够大,所得的频率可近似地当作事件A的概率。 注:随机事件的概率是频率的稳定值;频率是概率的近似值。3、求事件的概率的基本方法思考7:必然事件、不可能事件发生的概率分别为多少?概率的取值范围是什么? 4、概率的取值范围 统计事件A在n次实验中发生了m次,则P(A)=m/n 由于0≤m≤n,所以0≤m/n≤1,即0≤P(A)≤1注:(1)必然事件的概率:P(Ω)=1
(2)不可能事件的概率:P(Φ)=0
反之,也成立!三、数学应用例1.下面表中列出10次抛掷硬币的试验结果,n为每次试验抛掷硬币的次数, m为硬币正面向上的次数, 计算每次试验中“正面向上”这一事件的频率, 并考查其概率. 例2.某市统计近几年新生儿出生数及其中男婴数(单位:人)如下:(1)试计算男婴各年出生的频率(精确到0.001);
(2)该市男婴出生的概率是多少?三、数学应用解(1)1999年男婴出生的频率为:例3.在一场足球比赛中,A队获得了一次点球机会, 现A队有2名球负甲,乙想去主罚这次点球,已知这2名队负在此前的点球训练中的成绩如下表:乙:如课你是A队的主教练, 你认为安排甲和乙中的哪个队员去罚这个点球, 罚中的可能性会大些?甲:1.某篮球运动员在同一条件下进行投篮练习,结果如下表:计算表中进球的频率;
这位运动员投篮一次,进球的概率约是多少?(3)这位运动员进球的概率是0.8,那么他投10次篮一定能 投中8次吗?不一定. 投10次篮相当于做10次试验,每次试验的结果都是随机的, 所以投10次篮的结果也是随机的. 概率约是0.80.780.750.800.80 0.85 0.830.80四、学生活动四、学生活动 2、每道选择题有4个选择支,其中只有一个选择支是正确的。某次考试共有12道选择题,某人说:“每个选择支正确的概率是1/4,我每题都选择第一个选择支,则一定有3道题的选择结果正确。”这句话对吗?解:不对四、学生活动 3、掷一枚硬币,连续出现5次正面向上。张欣认为下次出现反面向上的概率大于1/2,你同意吗?为什么?解:不同意,随机事件的发生的概率与该事件以前是否发生无关,故下次发生的概率仍为1/2。四、学生活动4、某医院治疗一种疾病的治愈率为10%,那么,若前9个病人都没有治愈,第10个人就一定能治吗?解:如果把治疗一个病人作为一次试验,治愈率是10%,指随着试验次数的增加,即治疗病人数的增加,大约有10%的人能够治愈,对于一次试验来说,其结果是随机的,因此前9个人没治愈是可能的,对于第10个人来说,其结果仍然是随机的,即有可能治愈的,也可能没有治愈。五、课堂小结(一)知识1、频率、概率的定义及之间的联系2、随机事件的概率的求法
3、事件概率的取值范围(二)题型与方法1、求事件的概率:P(A)≈m/n2、概率的概念的巩固:定义法注意范围:0≤P(A)≤1
