沪科版数学七年级下册 6.1.1 平方根 课件(共20张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 6.1.1 平方根 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
6.1 平方根、立方根
第6章 实数
6.1.1 平方根
请你说一说解决问题的思路.
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
情境
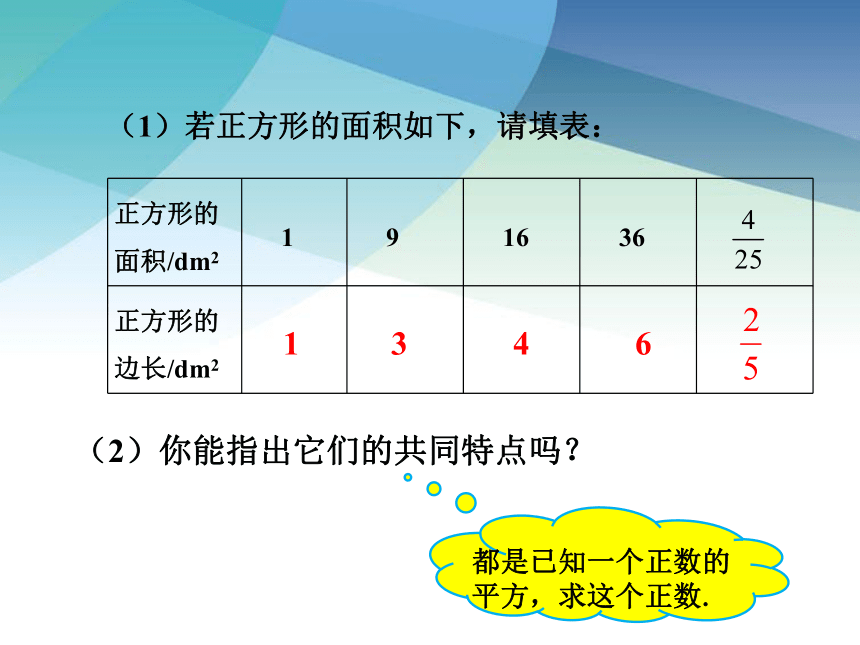
(1)若正方形的面积如下,请填表:
(2)你能指出它们的共同特点吗?
正方形的面积/dm2 1 9 16 36
正方形的边长/dm2
都是已知一个正数的平方,求这个正数.
1
3
4
6
如果一个数的平方等于9,这个数是多少?
想一想:3和-3有什么特征?
由于 ,
所以这个数是3或-3.
活动1:探究平方根的概念、性质及求法
探究
根据上面的研究过程填表:
如果我们把 分别叫做
的平方根,你能给出平方根的概念吗?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果
那么x叫做a的平方根.
归纳平方根的概念
例如:3和-3是9的平方根,
简记 是9的平方根.
5的平方根是
100的平方根是
9的平方根是
的平方根是
算一算
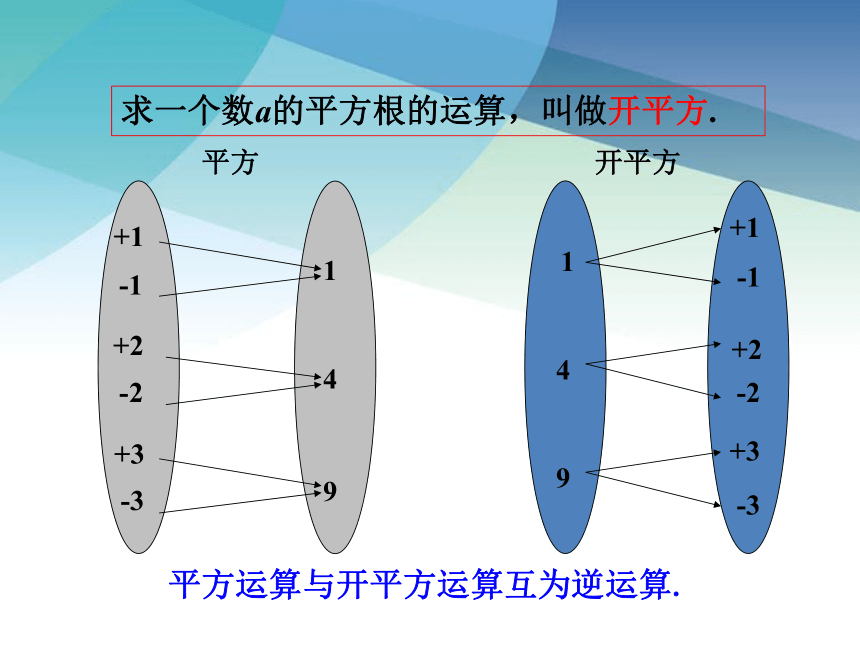
求一个数a的平方根的运算,叫做开平方.
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
平方运算与开平方运算互为逆运算.
例:下列各数有平方根吗?如果有,求出它的平方根,如
果没有,说明道理.
⑴64 ⑵ ⑶ 0.000196 ⑷-81
解:(1)∵(±8)2 =64
∴64的平方根是±8
即
(3)∵(0.014)2 =0.000196
∴0.000196的平方根是±0.014
即
(4)∵没有任何数的平方等于-81
∴-81 没有平方根
因为02=0,且任何不为0的数的平方都不等于0,所以0的平方根只有一个,它就是0本身.即: .
负数有平方根吗?因为正、负、0的平方都不是负数,所以负数没有平方根.
如: 无意义.
从上面看到,正数的平方根有两个,同学们能发现这两个数之间的关系吗?
正数的两个平方根互为相反数,
例:a的一个平方根是5,则另一个平方根是 ,a= .其中______ 是算术平方根.
-5
25
我们把正数的正的平方根叫做算术平方根.
5
活动2:探究算术平方根的概念、性质及求法
一个正数x的平方等于a,即 x2= a,这个正数x叫做a的算术平方根.
读作“根号a”
x2 = a (x为正数)
规定0的算术平方根是0,记作
也就是说,非负数的“算术”平方根是非负数;负数不存在算术平方根,即当 时, 无意义.
例:一个正数的平方根是2a+3和a-6你能知道a是多少吗?这个正数是几?
解:由平方根的意义知道
(2a+3)+(a-6)=0
得 a=1
这个正数是25.
例:填一填
(1)9的算数平方根是
(2) 的算数平方根是
(3) 0.01的算数平方根是
(4)10-6 的算数平方根是
(5)(-4)2 的算数平方根是
(6)10的算数平方根是
3
0.1
10-3
4
你知道下列各式中字母x的取值范围吗?
例:小明房间的面积为10.8平方米,房间地面恰由120块相同的正方形地砖铺成,问每块地砖的边长是多少?
解:设每块地砖的边长为x米,
由题意得:
(米)
答:每块的地砖的边长是0.3米.
解:(1)依次按键 3136
显示:56.
∴ .
(2) 依次按键 2
显示:1.414213562.
∴ .
例 用计算器求下列各式的值: (1) ; (2) (精确到 ).
活动3:探究用计算器求平方根
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果
那么x 叫做a的平方根.正数的两个平方根互为相反数.
0的平方根只有一个,它就是0本身.负数没有平方根.
一个正数x的平方等于a,即x2= a,这个正数x叫做a的算术平方根.
课堂小结
小结
6.1 平方根、立方根
第6章 实数
6.1.1 平方根
请你说一说解决问题的思路.
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
情境
(1)若正方形的面积如下,请填表:
(2)你能指出它们的共同特点吗?
正方形的面积/dm2 1 9 16 36
正方形的边长/dm2
都是已知一个正数的平方,求这个正数.
1
3
4
6
如果一个数的平方等于9,这个数是多少?
想一想:3和-3有什么特征?
由于 ,
所以这个数是3或-3.
活动1:探究平方根的概念、性质及求法
探究
根据上面的研究过程填表:
如果我们把 分别叫做
的平方根,你能给出平方根的概念吗?
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果
那么x叫做a的平方根.
归纳平方根的概念
例如:3和-3是9的平方根,
简记 是9的平方根.
5的平方根是
100的平方根是
9的平方根是
的平方根是
算一算
求一个数a的平方根的运算,叫做开平方.
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
平方运算与开平方运算互为逆运算.
例:下列各数有平方根吗?如果有,求出它的平方根,如
果没有,说明道理.
⑴64 ⑵ ⑶ 0.000196 ⑷-81
解:(1)∵(±8)2 =64
∴64的平方根是±8
即
(3)∵(0.014)2 =0.000196
∴0.000196的平方根是±0.014
即
(4)∵没有任何数的平方等于-81
∴-81 没有平方根
因为02=0,且任何不为0的数的平方都不等于0,所以0的平方根只有一个,它就是0本身.即: .
负数有平方根吗?因为正、负、0的平方都不是负数,所以负数没有平方根.
如: 无意义.
从上面看到,正数的平方根有两个,同学们能发现这两个数之间的关系吗?
正数的两个平方根互为相反数,
例:a的一个平方根是5,则另一个平方根是 ,a= .其中______ 是算术平方根.
-5
25
我们把正数的正的平方根叫做算术平方根.
5
活动2:探究算术平方根的概念、性质及求法
一个正数x的平方等于a,即 x2= a,这个正数x叫做a的算术平方根.
读作“根号a”
x2 = a (x为正数)
规定0的算术平方根是0,记作
也就是说,非负数的“算术”平方根是非负数;负数不存在算术平方根,即当 时, 无意义.
例:一个正数的平方根是2a+3和a-6你能知道a是多少吗?这个正数是几?
解:由平方根的意义知道
(2a+3)+(a-6)=0
得 a=1
这个正数是25.
例:填一填
(1)9的算数平方根是
(2) 的算数平方根是
(3) 0.01的算数平方根是
(4)10-6 的算数平方根是
(5)(-4)2 的算数平方根是
(6)10的算数平方根是
3
0.1
10-3
4
你知道下列各式中字母x的取值范围吗?
例:小明房间的面积为10.8平方米,房间地面恰由120块相同的正方形地砖铺成,问每块地砖的边长是多少?
解:设每块地砖的边长为x米,
由题意得:
(米)
答:每块的地砖的边长是0.3米.
解:(1)依次按键 3136
显示:56.
∴ .
(2) 依次按键 2
显示:1.414213562.
∴ .
例 用计算器求下列各式的值: (1) ; (2) (精确到 ).
活动3:探究用计算器求平方根
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.这就是说,如果
那么x 叫做a的平方根.正数的两个平方根互为相反数.
0的平方根只有一个,它就是0本身.负数没有平方根.
一个正数x的平方等于a,即x2= a,这个正数x叫做a的算术平方根.
课堂小结
小结
