青岛版七年级下册数学第9章《平行线》复习课件 (共28张PPT)
文档属性
| 名称 | 青岛版七年级下册数学第9章《平行线》复习课件 (共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 22:24:11 | ||
图片预览







文档简介
(共28张PPT)
青岛版七年级下册
情境引入
数学来源于生活,生活中处处有数学。
1. 会用平行线的有关概念、性质和判定
进行简单的推理或计算。
2. 对性质和判定的运用更加系统化、条理
化,并能在适当的时候添加辅助线。
3. 能将复杂图形转化为基本图形,学会图
形语言、符号语言、几何语言的转化。
1.判断对错:
(1) 不相交的两条直线叫平行线。( )
(2) 经过一点有且只有一条直线,与已知直线
平行。( )
(3) 两条直线被第三条直线所截,同位角相
等。( )
(4) 平行于同一条直线的两直线平行。( )
(5) 垂直于同一条直线的两直线平行。( )
×
√
×
×
×
课前复习案
2.如图,补全下面的说理过程
∵∠1=∠2
∴______ ∥________ ( )
c
a
b
1
2
3
4
(2) ∵∠1=∠3
∴______∥_______( )
(3)∵∠1+∠4=180°
∴______∥________
( )
a
b
同位角相等,两直线平行
a
b
内错角相等,两直线平行
a
b
同旁内角互补,两直线平行
A
B
C
D
E
1
2
3
4
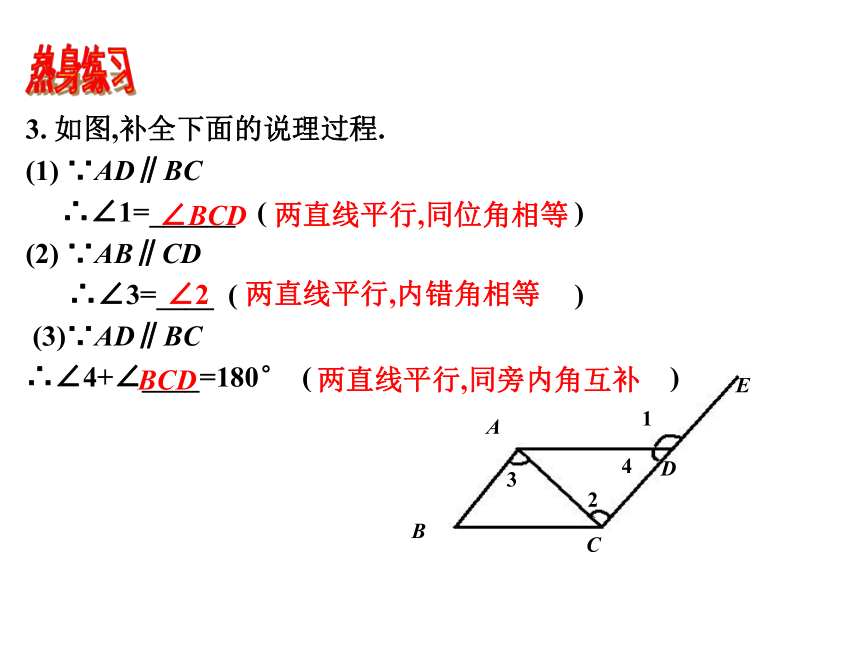
3. 如图,补全下面的说理过程.
(1) ∵AD∥BC
∴∠1=______ ( )
(2) ∵AB∥CD
∴∠3=____ ( )
(3)∵AD∥BC
∴∠4+∠____=180° ( )
∠BCD
∠2
BCD
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
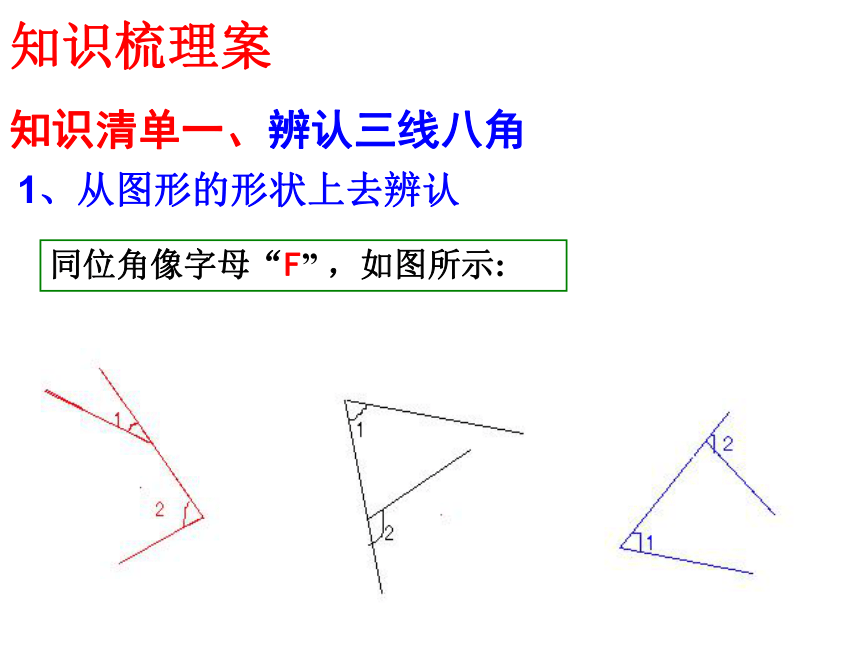
同位角像字母“F” ,如图所示:
知识清单一、辨认三线八角
1、从图形的形状上去辨认
知识梳理案
内错角像字母“Z” ,如图所示:
同旁内角像字母“U” ,如图所示:
2、从图形的位置特点去辨认
温馨提示:判断角的类型应先找到“截线”,再找另外两条直线(即被截线)然后再根据位置特点决定是哪一种角.
三线八角
同位角(同侧,同旁)
内错角(内部,交错)
同旁内角(内部,同旁)
知识清单二:两个重要概念
1.平行线:
2.两条平行线
之间的距离:
如果两条直线平行,那么其中
一条直线上每个点到另一条
直线的距离都相等。这个距离,
叫做这两条平行线之间的距离。
在同一平面内,不相交的两条直线叫平行线。
用直尺和三角板画平行线的依据:
同位角相等,两直线平行
www.1230.org 初中数学资源网
平行线的判定 平行线的性质
条件 结论 条件 结论
同位角相等 两直线平行 两直线平行 同位角相等
内错角相等 内错角相等
同旁内角互补 同旁内角互补
知识清单三:平行线的性质和判定
平行线的性质
由“线”定“角”
平行线的判定
由“角”定“线”
www.1230.org 初中数学资源网
平行线的判定 平行线的性质
条件 结论 条件 结论
同位角相等 两直线平行 两直线平行 同位角相等
内错角相等 内错角相等
同旁内角互补 同旁内角互补
知识清单三:平行线的性质和判定
温馨提示:
平行于同一条直线的两直线平行。
在同一平面内,垂直于同一条直线的两直线平行。
知识清单四:转折角的识记
A
E
B
D
C
结论:
∠E= ∠B+ ∠D
AB∥CD
微课助学1
B
E
D
C
A
结论:
∠E+∠A+∠C=360°
微课助学2
www.1230.org 初中数学资源网
例1 : 如图,BD⊥AC,EF⊥AC,D、F分别为垂足,∠1=∠2,试说明∠ADG =∠C 。
3
解:∵ BD⊥AC,EF⊥AC
∴ ∠DCA=∠CAB= 90°
∴ EF∥ BD
∴ ∠2=∠3
又∵ ∠1=∠2
∴ ∠1=∠3
∴ DG∥ CB
∴ ∠ADG =∠C
课中探究案
典例分析
例2:如图,已知AB ∥ CD, ∠1=∠2,那么∠E与∠F相等吗?试作出判断并说出你的理由。
1
2
3
4
A
B
C
D
E
F
典例分析
解:∠E=∠F
理由如下:
∵ AB ∥ CD
∴ ∠DCA=∠CAB
又∵ ∠1=∠2
∴∠3=∠4
∴ CE∥ AF
∴ ∠E=∠F
1、已知∠DAF= ∠AFE, ∠ADC+ ∠DCB =180°.求证: BC∥EF.
证明:∵ ∠DAF= ∠AFE
∴ AD∥EF.
又∵ ∠ADC+ ∠DCB =180°.
∴ AD∥BC.
∴ BC∥EF.
能力提升
能力提升
2、如图,AB∥CD,EF⊥CD ,
∠1=50° .求 ∠2的度数。
解:∵ AB∥CD
∴ ∠3 = ∠1.
又∵ ∠1=50°,
∴ ∠3= 50°.
又∵ EF⊥CD ,
∴ ∠CFE = 90°.
∴ ∠2 = 90°-50°= 40°
3
通过本节课的学习:
我知道了……
我学会了……
我体会到了……
2.平行线的三个性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
3.平行线的三个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
1.平行线的定义
在同一平面内不相交的两条直线叫做平行线。
平行线的性质与判定
温馨提示:
平行于同一条直线的两直线平行。
在同一平面内,垂直于同一条直线的两直线平行。
1.如图,已知AB∥CD,∠1=30°,
∠2=90°,
则∠3等于( )
达标检测案
(相信自己肯定行!)
60°
2.如图: AB∥CD, CE平分 ∠ACD,
∠A =110°,则∠ECD的度数为( ).
A.110°
B.70°
C.55°
D.35°
D
3.如图:点E在BC的延长线上,下列四个
条件中,不能判定AB∥CD的是( )
A.∠2 = ∠3
B.∠B = ∠DCE
C.∠1 = ∠4
D. ∠D+ ∠DAB =180°
太棒了,继续努力!
C
www.1230.org 初中数学资源网
5、若两条平行线被第三条直线所截,则一组内错角的平分线互相( )
A 垂直 B 平行 C 重合 D 相交
4 、两条直线被第三条直线所截,则( )
A 同位角相等 B 同旁内角互补
C 内错角相等 D 以上都不对
D
B
6. 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有( )个.
A. 2
B. 3
C. 4
D. 5
A
B
C
D
E
F
O
D
真正的考验来啦!
D
作业:
P45(4、5、9、10)
时光飞逝,每一天应该思考自己做了些什么,是‘正号’还是‘负号’,倘若是‘+’号,则进步;倘若是‘-’号,就要吸取教训,采取措施,才能迎头赶上。
结束语
青岛版七年级下册
情境引入
数学来源于生活,生活中处处有数学。
1. 会用平行线的有关概念、性质和判定
进行简单的推理或计算。
2. 对性质和判定的运用更加系统化、条理
化,并能在适当的时候添加辅助线。
3. 能将复杂图形转化为基本图形,学会图
形语言、符号语言、几何语言的转化。
1.判断对错:
(1) 不相交的两条直线叫平行线。( )
(2) 经过一点有且只有一条直线,与已知直线
平行。( )
(3) 两条直线被第三条直线所截,同位角相
等。( )
(4) 平行于同一条直线的两直线平行。( )
(5) 垂直于同一条直线的两直线平行。( )
×
√
×
×
×
课前复习案
2.如图,补全下面的说理过程
∵∠1=∠2
∴______ ∥________ ( )
c
a
b
1
2
3
4
(2) ∵∠1=∠3
∴______∥_______( )
(3)∵∠1+∠4=180°
∴______∥________
( )
a
b
同位角相等,两直线平行
a
b
内错角相等,两直线平行
a
b
同旁内角互补,两直线平行
A
B
C
D
E
1
2
3
4
3. 如图,补全下面的说理过程.
(1) ∵AD∥BC
∴∠1=______ ( )
(2) ∵AB∥CD
∴∠3=____ ( )
(3)∵AD∥BC
∴∠4+∠____=180° ( )
∠BCD
∠2
BCD
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
同位角像字母“F” ,如图所示:
知识清单一、辨认三线八角
1、从图形的形状上去辨认
知识梳理案
内错角像字母“Z” ,如图所示:
同旁内角像字母“U” ,如图所示:
2、从图形的位置特点去辨认
温馨提示:判断角的类型应先找到“截线”,再找另外两条直线(即被截线)然后再根据位置特点决定是哪一种角.
三线八角
同位角(同侧,同旁)
内错角(内部,交错)
同旁内角(内部,同旁)
知识清单二:两个重要概念
1.平行线:
2.两条平行线
之间的距离:
如果两条直线平行,那么其中
一条直线上每个点到另一条
直线的距离都相等。这个距离,
叫做这两条平行线之间的距离。
在同一平面内,不相交的两条直线叫平行线。
用直尺和三角板画平行线的依据:
同位角相等,两直线平行
www.1230.org 初中数学资源网
平行线的判定 平行线的性质
条件 结论 条件 结论
同位角相等 两直线平行 两直线平行 同位角相等
内错角相等 内错角相等
同旁内角互补 同旁内角互补
知识清单三:平行线的性质和判定
平行线的性质
由“线”定“角”
平行线的判定
由“角”定“线”
www.1230.org 初中数学资源网
平行线的判定 平行线的性质
条件 结论 条件 结论
同位角相等 两直线平行 两直线平行 同位角相等
内错角相等 内错角相等
同旁内角互补 同旁内角互补
知识清单三:平行线的性质和判定
温馨提示:
平行于同一条直线的两直线平行。
在同一平面内,垂直于同一条直线的两直线平行。
知识清单四:转折角的识记
A
E
B
D
C
结论:
∠E= ∠B+ ∠D
AB∥CD
微课助学1
B
E
D
C
A
结论:
∠E+∠A+∠C=360°
微课助学2
www.1230.org 初中数学资源网
例1 : 如图,BD⊥AC,EF⊥AC,D、F分别为垂足,∠1=∠2,试说明∠ADG =∠C 。
3
解:∵ BD⊥AC,EF⊥AC
∴ ∠DCA=∠CAB= 90°
∴ EF∥ BD
∴ ∠2=∠3
又∵ ∠1=∠2
∴ ∠1=∠3
∴ DG∥ CB
∴ ∠ADG =∠C
课中探究案
典例分析
例2:如图,已知AB ∥ CD, ∠1=∠2,那么∠E与∠F相等吗?试作出判断并说出你的理由。
1
2
3
4
A
B
C
D
E
F
典例分析
解:∠E=∠F
理由如下:
∵ AB ∥ CD
∴ ∠DCA=∠CAB
又∵ ∠1=∠2
∴∠3=∠4
∴ CE∥ AF
∴ ∠E=∠F
1、已知∠DAF= ∠AFE, ∠ADC+ ∠DCB =180°.求证: BC∥EF.
证明:∵ ∠DAF= ∠AFE
∴ AD∥EF.
又∵ ∠ADC+ ∠DCB =180°.
∴ AD∥BC.
∴ BC∥EF.
能力提升
能力提升
2、如图,AB∥CD,EF⊥CD ,
∠1=50° .求 ∠2的度数。
解:∵ AB∥CD
∴ ∠3 = ∠1.
又∵ ∠1=50°,
∴ ∠3= 50°.
又∵ EF⊥CD ,
∴ ∠CFE = 90°.
∴ ∠2 = 90°-50°= 40°
3
通过本节课的学习:
我知道了……
我学会了……
我体会到了……
2.平行线的三个性质:
两直线平行
同位角相等
内错角相等
同旁内角互补
3.平行线的三个判定:
两直线平行
同位角相等
内错角相等
同旁内角互补
1.平行线的定义
在同一平面内不相交的两条直线叫做平行线。
平行线的性质与判定
温馨提示:
平行于同一条直线的两直线平行。
在同一平面内,垂直于同一条直线的两直线平行。
1.如图,已知AB∥CD,∠1=30°,
∠2=90°,
则∠3等于( )
达标检测案
(相信自己肯定行!)
60°
2.如图: AB∥CD, CE平分 ∠ACD,
∠A =110°,则∠ECD的度数为( ).
A.110°
B.70°
C.55°
D.35°
D
3.如图:点E在BC的延长线上,下列四个
条件中,不能判定AB∥CD的是( )
A.∠2 = ∠3
B.∠B = ∠DCE
C.∠1 = ∠4
D. ∠D+ ∠DAB =180°
太棒了,继续努力!
C
www.1230.org 初中数学资源网
5、若两条平行线被第三条直线所截,则一组内错角的平分线互相( )
A 垂直 B 平行 C 重合 D 相交
4 、两条直线被第三条直线所截,则( )
A 同位角相等 B 同旁内角互补
C 内错角相等 D 以上都不对
D
B
6. 已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中与∠EOD相等的角有( )个.
A. 2
B. 3
C. 4
D. 5
A
B
C
D
E
F
O
D
真正的考验来啦!
D
作业:
P45(4、5、9、10)
时光飞逝,每一天应该思考自己做了些什么,是‘正号’还是‘负号’,倘若是‘+’号,则进步;倘若是‘-’号,就要吸取教训,采取措施,才能迎头赶上。
结束语
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
