沪科版八年级下册 19.2.4 三角形、梯形中位线的应用 教案
文档属性
| 名称 | 沪科版八年级下册 19.2.4 三角形、梯形中位线的应用 教案 | 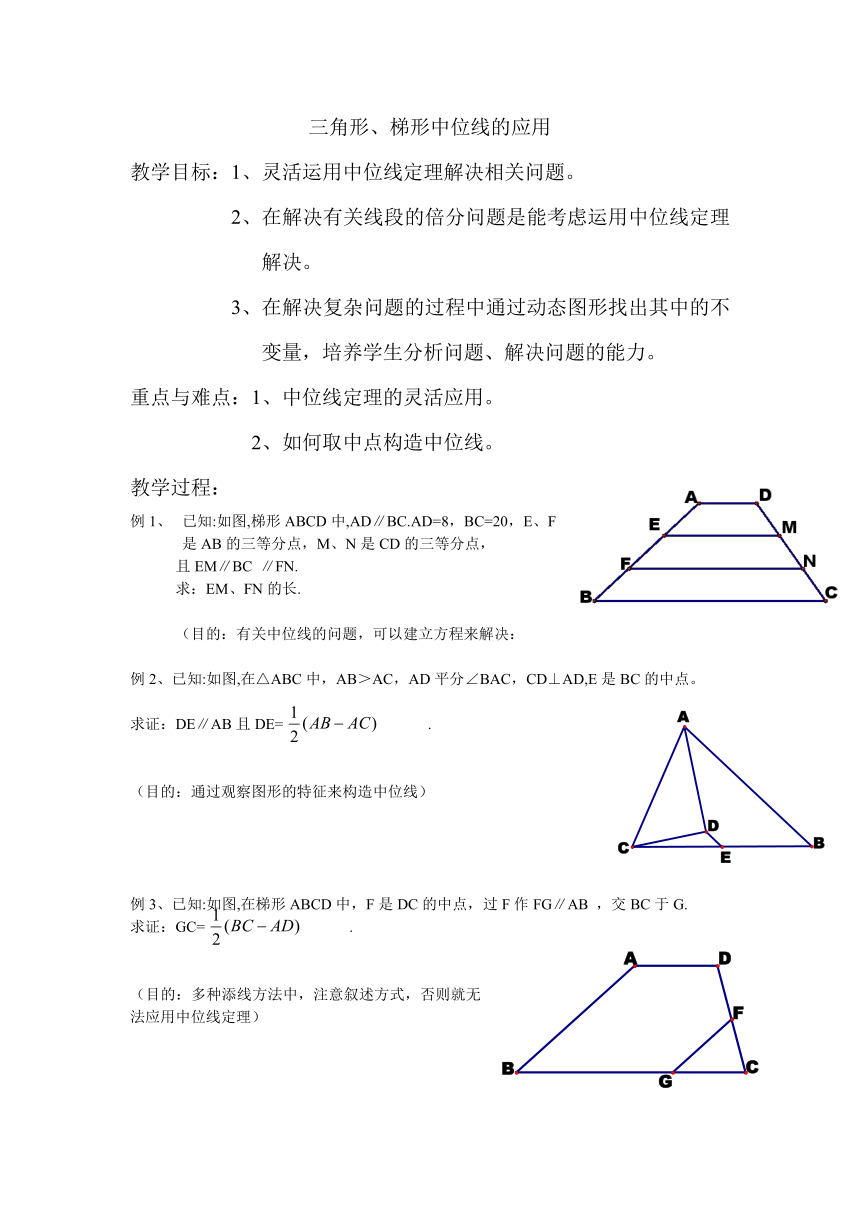 | |
| 格式 | doc | ||
| 文件大小 | 31.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 09:42:49 | ||
图片预览

文档简介
三角形、梯形中位线的应用
教学目标:1、灵活运用中位线定理解决相关问题。
2、在解决有关线段的倍分问题是能考虑运用中位线定理解决。
3、在解决复杂问题的过程中通过动态图形找出其中的不变量,培养学生分析问题、解决问题的能力。
重点与难点:1、中位线定理的灵活应用。
2、如何取中点构造中位线。
教学过程:
例1、 已知:如图,梯形ABCD中,AD∥BC.AD=8,BC=20,E、F是AB的三等分点,M、N是CD的三等分点,
且EM∥BC ∥FN.
求:EM、FN的长.
(目的:有关中位线的问题,可以建立方程来解决:
例2、已知:如图,在△ABC中,AB>AC,AD平分∠BAC,CD⊥AD,E是BC的中点。
求证:DE∥AB且DE= .
(目的:通过观察图形的特征来构造中位线)
例3、已知:如图,在梯形ABCD中,F是DC的中点,过F作FG∥AB ,交BC于G.
求证:GC= .
(目的:多种添线方法中,注意叙述方式,否则就无 法应用中位线定理)
例4、已知如图:在四边形ABCD中,AC=BD,且相较于点O,E、F分别是AB、CD的中点,EF分别交AC、BD于点G、H.
求证:OG=OH
(目的:有两个中点,又无法构成中位线时,可以考虑再取中 点,构成中位线,取中点时注意结合已知条件)
例5、已知:如图,在四边形ABCD中,AD=BC, F、M分别是CD 、AB的中点,AD、MF的延长线交于点G,MF、BC的延长线交于点E.
求证:∠DGF=∠CEF.
(目的:对前面知识的巩固和运用)
思考:已知在Rt ABC中,AB=BC,在 Rt ADE中,AD=DE,联结EC,取EC的中点M,联结DM和BM.
(1)若点D在边AC上,点E在边AB上,且与点B不重合,(如左图)
求证:BM=DM,BM⊥DM;
(2)如果将上题中的 ADE绕点A逆时针旋转小于45°的角,
那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给出证明。
(目的:培养学生的综合能力)
知识总结:见PPt
作业:练习卷
教学目标:1、灵活运用中位线定理解决相关问题。
2、在解决有关线段的倍分问题是能考虑运用中位线定理解决。
3、在解决复杂问题的过程中通过动态图形找出其中的不变量,培养学生分析问题、解决问题的能力。
重点与难点:1、中位线定理的灵活应用。
2、如何取中点构造中位线。
教学过程:
例1、 已知:如图,梯形ABCD中,AD∥BC.AD=8,BC=20,E、F是AB的三等分点,M、N是CD的三等分点,
且EM∥BC ∥FN.
求:EM、FN的长.
(目的:有关中位线的问题,可以建立方程来解决:
例2、已知:如图,在△ABC中,AB>AC,AD平分∠BAC,CD⊥AD,E是BC的中点。
求证:DE∥AB且DE= .
(目的:通过观察图形的特征来构造中位线)
例3、已知:如图,在梯形ABCD中,F是DC的中点,过F作FG∥AB ,交BC于G.
求证:GC= .
(目的:多种添线方法中,注意叙述方式,否则就无 法应用中位线定理)
例4、已知如图:在四边形ABCD中,AC=BD,且相较于点O,E、F分别是AB、CD的中点,EF分别交AC、BD于点G、H.
求证:OG=OH
(目的:有两个中点,又无法构成中位线时,可以考虑再取中 点,构成中位线,取中点时注意结合已知条件)
例5、已知:如图,在四边形ABCD中,AD=BC, F、M分别是CD 、AB的中点,AD、MF的延长线交于点G,MF、BC的延长线交于点E.
求证:∠DGF=∠CEF.
(目的:对前面知识的巩固和运用)
思考:已知在Rt ABC中,AB=BC,在 Rt ADE中,AD=DE,联结EC,取EC的中点M,联结DM和BM.
(1)若点D在边AC上,点E在边AB上,且与点B不重合,(如左图)
求证:BM=DM,BM⊥DM;
(2)如果将上题中的 ADE绕点A逆时针旋转小于45°的角,
那么(1)中的结论是否仍成立?如果不成立,请举出反例;如果成立,请给出证明。
(目的:培养学生的综合能力)
知识总结:见PPt
作业:练习卷
