2022年强化训练华东师大版七年级数学下册第6章一元一次方程练习试卷 (word版含答案)
文档属性
| 名称 | 2022年强化训练华东师大版七年级数学下册第6章一元一次方程练习试卷 (word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 458.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览




文档简介
七年级数学下册第6章一元一次方程专项练习
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、若是关于的方程的解,则的值为( )
A.3 B.-3 C.1 D.-1
2、如果,那么下列等式不一定成立的是( )
A. B. C. D.
3、若a=b,m是任意实数,则下列等式不一定成立的是( )
A.a+m=b+m B.a﹣m=b﹣m C.am=bm D.
4、已知下列方程:①;②x+y;③x=0; ④x2+4x;⑤﹣3;⑥x(1﹣2x)=3x﹣1.其中是一元一次方程的是( )
A.①⑤ B.①③ C.①③⑥ D.⑤⑥
5、将正整数1至6000按一定规律排列如右表:同时平移表中带阴影的方框,方框中三个数的和可能是( )
A.116 B.117 C.129 D.138
6、已知a,x为正整数,若ax﹣1=x+7,则满足条件的所有a的值之和为( )
A.15 B.17 C.19 D.21
7、下列说法中,一定正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
8、幻方最早起源于中国,在《自然科学大事年表》中,对幻方做了特别的述说:“公元前一世纪,《大戴礼》记载,中国古代有象征吉祥的河图、洛书、纵横图,即为九宫算,被认为是现代组合数学最古老的发现”.请将,,,,,,,,分别填入如图所示的幻方中,要求同一横行、同一竖行以及同一条斜对角线上的3个数相加都得0,则x+y的值为( )
A. B. C. D.
9、已知是方程的解,则a的值是( )
A.36 B. C.4 D.
10、下列各式中,是一元一次方程的是( )
A.3x-5 B. C. D.5x-3y=0
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、若将数轴折叠,使得表示-1的点与表示5的点重合,则原点与表示_______的点重合.
2、某课外活动小组中女生人数占全组人数的一半,如果增加6名女生,那么女生人数就占全组人数的.设该课外活动小组共有x人,则可列方程为________.
3、五一期间,旅行社组织老师和学生共50人的旅行团去旅游,景区门票售价标准为:成人票50元/张,学生票20元/张,该旅行团购买门票共花费1900元,则该旅行团有老师 _____人.
4、已知点、在数轴上,点表示的数为-5,点表示的数为15.动点从点出发,以每秒3个单位长度的速度沿数轴正方向匀速移动,则点移动__________秒后,.
5、已知是方程的解,则a的值是______.
三、解答题(5小题,每小题10分,共计50分)
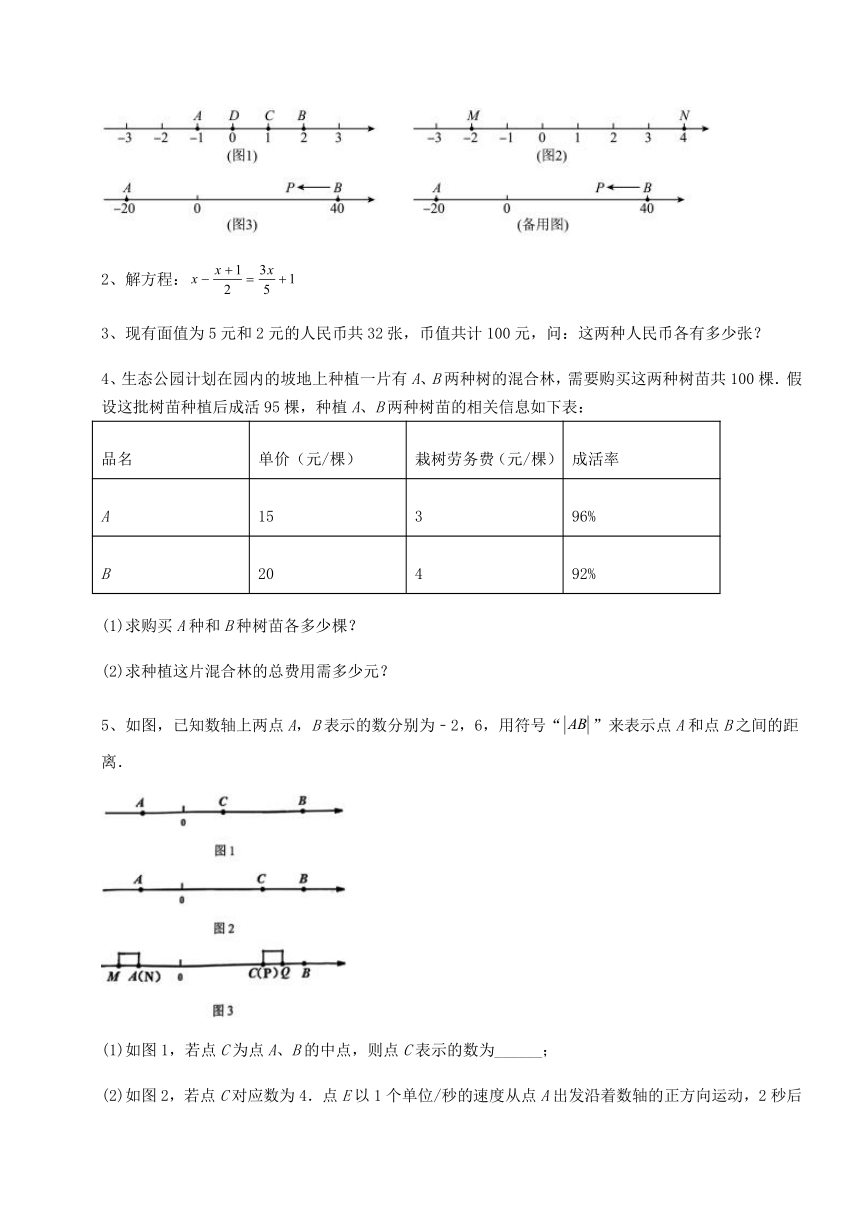
1、阅读理解:若、、为数轴上三点,若点到的距离是点到的距离的倍,即满足 时,则称点是“对的相关点”.例如,当点、、 表示的数分别为0,1,2时,,则称点是“对的2相关点”.
(1)如图1,点表示的数为,点表示的数为2.表示1的点到点的距离是2,到点的距离是1,那么点是“对的2相关点”;又如,表示0的点到点的距离是1,到点的距离是2,那么点 “对的2相关点”,但点 “对的2相关点”;(请在横线上填是或不是);
(2)如图2,、为数轴上两点,点所表示的数为,点所表示的数为4.在数轴上,数 所表示的点是“对的3相关点”;
(3)如图3,、为数轴上两点,点A所表示的数为,点B所表示的数为40.现有一只电子蚂蚁从点出发,以每秒4个单位的速度向左运动,到达点A停止.当经过多少秒时,、和中恰有一个点为“其余两点中一点对另一点的2相关点”?
2、解方程:
3、现有面值为5元和2元的人民币共32张,币值共计100元,问:这两种人民币各有多少张?
4、生态公园计划在园内的坡地上种植一片有A、B两种树的混合林,需要购买这两种树苗共100棵.假设这批树苗种植后成活95棵,种植A、B两种树苗的相关信息如下表:
品名 单价(元/棵) 栽树劳务费(元/棵) 成活率
A 15 3 96%
B 20 4 92%
(1)求购买A种和B种树苗各多少棵?
(2)求种植这片混合林的总费用需多少元?
5、如图,已知数轴上两点A,B表示的数分别为﹣2,6,用符号“”来表示点A和点B之间的距离.
(1)如图1,若点C为点A、B的中点,则点C表示的数为______;
(2)如图2,若点C对应数为4.点E以1个单位/秒的速度从点A出发沿着数轴的正方向运动,2秒后点F以2个单位/秒的速度从点C出发也沿着数轴的正方向运动,点F到达B点处立刻按原速返回沿着数轴的负方向运动,直到点E到达点B,两个点同时停止运动.设点E运动的时间为t(),在此过程中存在t使得成立,求t的值;
(3)如图3,若点C对应数为4.长度均为1个单位的电子虫MN和电子虫PQ,其中MN从点A出发(点N与点A重合)以1个单位/秒的速度沿着数轴的正方向运动,同时PQ从点C出发(点P与点C重合)以2个单位/秒的速度沿着数轴的负方向运动,当PQ运动到点P与点A重合时,PQ保持速度不变,反向沿着数轴正方向运动,当点Q运动到点M重合时,两电子虫都停止运动.在运动过程中,如果出现两条电子虫有重叠的时候,它们各自运动方向不变但速度会减半,重叠结束速度立即恢复.设电子虫MN运动时间为t秒,是否存在,使两电子虫上的点N和点P刚好相距3个单位长度,若存在,请直接写出t的值.若不存在,请说明理由.
-参考答案-
一、单选题
1、D
【解析】
【分析】
根据方程的解的定义,将代入方程得到关于的一元一次方程,解方程求解即可.
【详解】
解:∵是关于的方程的解,
∴
解得
故选D
【点睛】
本题考查了一元一次方程的解,解一元一次方程,掌握方程的解的定义是解题的关键.使方程左右两边的值相等的未知数的值是该方程的解.
2、D
【解析】
【分析】
根据等式的性质逐项分析即可.
【详解】
解:A. ∵,∴,故成立;
B. ∵,∴,故成立;
C. ∵,∴,故成立;
D. ∵,当m≠0时,,故不一定成立;
故选D.
【点睛】
本题考查了等式的基本性质,正确掌握等式的性质是解题的关键.等式的基本性质1是等式的两边都加上(或减去)同一个整式,所得的结果仍是等式;等式的基本性质2是等式的两边都乘以(或除以)同一个数(除数不能为0),所得的结果仍是等式.
3、D
【解析】
【分析】
根据等式的性质即可求出答案.
【详解】
解:A、利用等式性质1,两边都加m,得到a+m=b+m,原变形一定成立,故此选项不符合题意;
B、利用等式性质1,两边都减去m,得到a﹣m=b﹣m,原变形一定成立,故此选项不符合题意;
C、利用等式性质2,两边都乘m,得到am=bm,原变形一定成立,故此选项不符合题意;
D、成立的条件是m≠0,原变形不一定成立,故此选项符合题意;
故选:D.
【点睛】
本题考查了等式的性质,掌握等式的性质是解题的关键.等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数(或式子),结果仍相等.
4、B
【解析】
【分析】
由一元一次方程的概念可知:①含有一个未知数,②未知数的次数为1,③整式方程,据此进行判断即可.
【详解】
解::①是一元一次方程;
②x+y不是方程;
③x=0 是一元一次方程
④x2+4x不是方程;
⑤﹣3不是一元一次方程;
⑥x(1﹣2x)=3x﹣1,不是一元一次方程
故①③是一元一次方程,
故选B
【点睛】
本题考查了一元一次方程的概念,理解一元一次方程的概念是解题的关键.
5、A
【解析】
【分析】
设最左边数为x,则另外两个数分别为x+2、x+9,进而可得出三个数之和为3x+11,令其分别等于四个选项中数,解之即可得出x的值,由x为整数、x不能为第七列及第八列数,即可得到答案.
【详解】
解:设最左边数为x,则另外两个数分别为x+2、x+9,
∴三个数之和为x+x+2+x+9=3x+11.
根据题意得:3x+11=116,3x+11=117,3x+11=129,3x+11=138,
解得:x=35,x=(舍去),x=(舍去),x=(舍去),
故选:A.
【点睛】
本题考查了一元一次方程的应用以及规律型中数字的变化类,找准等量关系,正确列出一元一次方程是解题的关键.
6、C
【解析】
【分析】
移项,合并同类项,系数化为1,解原方程,根据x为正整数,得到几个关于a的一元一次方程,解之,求出a的值,相加求和即可得到答案.
【详解】
解:ax 1=x+7,
移项得:ax x=7+1,
合并同类项得:(a 1)x=8,
若a=1,则0=8,(无意义,舍去),
若a≠1,则x=,
∵x为正整数,
∴a 1=1或2或4或8,
解得:a=2或3或5或9,
∴a的值的和为:2+3+5+9=19,
故选C.
【点睛】
本题考查了一元一次方程的解,正确掌握解一元一次方程的方法是解题的关键.
7、A
【解析】
【分析】
根据等式两边同时乘以可对进行判断;利用等式两边同时除以c可对进行判断;利用平方根的定义对进行判断;根据等式的性质对进行判断.
【详解】
解:.若,则,所以选项符合题意;
.若,当时,,所以选项不符合题意;
.若,则或,所以选项不符合题意;
.若,则,所以选项不符合题意.
故选:.
【点睛】
本题考查了等式的性质:等式两边同时加上或减去同一个整式,等式仍然成立;等式两边同时乘或除以同一个不为0的整式,等式仍然成立.
8、B
【解析】
【分析】
设如图所示的幻方中y右边的方格中的数为z,根据“同一横行、同一竖行以及同一条斜对角线上的3个数相加都得0”可得,,,求出和的值,然后代入即可求出x+y的值.
【详解】
解:设如图所示的幻方中y右边的方格中的数为z,
∵同一横行、同一竖行以及同一条斜对角线上的3个数相加都得0,
∴,解得:,
又∵,将代入得:,
又∵,将代入得:,
∴.
故选:B.
【点睛】
此题考查了幻方的性质,代数式求值问题,解一元一次方程等知识,解题的关键是根据幻方中的规律列方程求出和的值.
9、A
【解析】
【分析】
把代入方程得到一个关于a的方程,从而求解.
【详解】
解:把代入方程,
得:,
解得:a=36,
故选:A.
【点睛】
本题考查了解一元一次方程以及方程的解的定义(方程两边左右相等的未知数的值叫做方程的解),理解定义是解题关键.
10、C
【解析】
【分析】
利用一元一次方程的定义进行解答即可.
【详解】
解:A、不是等式,所以不是一元一次方程,故此选项不合题意;
B、含有分式,不是一元一次方程,故此选项不合题意;
C、是一元一次方程,故此选项符合题意;
D、含有两个未知数,不是一元一次方程,故此选项不合题意;
故选:C.
【点睛】
此题主要考查了一元一次方程定义,关键是掌握一元一次方程属于整式方程,即方程两边都是整式.一元指方程仅含有一个未知数,一次指未知数的次数为1,且未知数的系数不为0.
二、填空题
1、4
【解析】
【分析】
设原点与表示x的点重合,先根据题意求出数轴上折叠的那个地方表示的数为,则,由此即可得到答案.
【详解】
解:设原点与表示x的点重合,
∵将数轴折叠,使得表示-1的点与表示5的点重合,
∴数轴上折叠的那个地方表示的数为,
∴,
解得,
故答案为:4.
【点睛】
本题主要考查了数轴上两点中点的计算方法,解一元一次方程,解题的关键在于能够根据题意求出折叠点表示的数.
2、
【解析】
【分析】
设小组原有人,则女生原有人,根据增加6名女生后就占全组的人数的,即可得出关于的一元一次方程,此题得解.
【详解】
解:设小组原有人,则女生原有人,
依题意得:.
故答案为:.
【点睛】
本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.
3、
【解析】
【分析】
设该旅行团有老师人,则有学生人,根据题意列一元一次方程解方程求解即可.
【详解】
解:设该旅行团有老师人,则有学生人,根据题意得,
解得
该旅行团有老师人
故答案为:
【点睛】
本题考查了一元一次方程的应用,根据题意列出方程是解题的关键.
4、5或10
【解析】
【分析】
分两种情况讨论,当点P在点B的左侧或点P在点B的右侧,再根据数轴上两点间的距离列方程解题.
【详解】
解:设t秒后,,此时点P表示的数为:-5+3t
分两种情况讨论,
①当点P在点B的左侧时,
;
②点P在点B的右侧,
综上所述,当或时,,
故答案为:5或10.
【点睛】
本题考查数轴上的动点问题、数轴上两点间的距离等知识,涉及一元一次方程,是重要考点,掌握相关知识是解题关键.
5、4
【解析】
【分析】
把代入方程得到关于的一元一次方程,依次去括号,移项,合并同类项,系数化为1,即可得到答案.
【详解】
解:把代入方程得:
,
去括号得:,
系数化为1得:,
故答案为:4.
【点睛】
本题考查了一元一次方程的解,解题的关键是正确掌握解一元一次方程的方法.
三、解答题
1、(1)不是,是;(2)或7;(3)5秒或7.5或10秒
【解析】
【分析】
(1)根据“A对B的2相关点”的定义和“B对A的2相关点”即可求解;
(2)根据“M对N的3相关点”的定义列方程即可求解;
(3)根据题意得:PB=4t,AB=40+20=60,PA=60-4t,由“A对B的2相关点”的定义可知:分两种情况列式:①PB=2PA;②PA=2PB;可以得出结论.
【详解】
解:(1)∵表示0的点D到点A的距离是1,到点B的距离是2,
那么点D不是“A对B的2相关点”,但点D是“B对A的2相关点”;
故答案为:不是,是;
(2)∵点M所表示的数为-2,点N所表示的数为4.设点C的坐标为x,
依题意得:,
解得:x=或7,
∴数或7所表示的点是“M对N的3相关点”;
故答案为:或7;
(3)由题意得:PB=4t,AB=40+20=60,PA=60-4t,
点P走完所用的时间为:60÷4=15(秒),
分四种情况:
①当PA=2PB时,即2×4t=60-4t,t=5(秒),P是“A对B的2相关点”,
②当PB=2PA时,即4t=2(60-4t),t=10(秒),P是“B对A的2相关点”,
③当AB=2PB时,即60=2×4t,t=7.5(秒),B是“A对P的2相关点”,
④当AB=2AP时,即60=2(60-4t),t=7.5(秒),A是“B对P的2相关点”,
∴当经过5秒或7.5或10秒时,P、A和B中恰有一个点为“其余两点中一点对另一点的2相关点”.
【点睛】
本题考查了数轴及数轴上两点的距离、动点问题,熟练掌握动点中三个量的数量关系式:路程=时间×速度,认真理解新定义是解题的关键.
2、
【解析】
【分析】
解一元一次方程,先去分母、去括号,然后移项合并同类项,最后系数化为1即可.
【详解】
解:去分母:
去括号:
移项:
合并同类项:
系数化为1:
∴是原方程的解.
【点睛】
本题考查了解一元一次方程.解题的关键在于去分母,去括号.
3、面值为5元得人民币由12张,面值为2元得人民币由20张.
【解析】
【分析】
设面值为5元得人民币由张,面值为2元得人民币由张,然后由面值共100元,列出方程,解方程即可.
【详解】
解答:解:设面值为5元得人民币由张,面值为2元得人民币由张,
根据题意得:,
解得:(张,
(张.
答:面值为5元得人民币由12张,面值为2元得人民币由20张.
【点睛】
此题属于一元一次方程的应用题,关键是由题意列出方程.
4、 (1)购买A种树苗75棵,购买B种树苗25棵;
(2)种植这片混合林的总费用需1950元.
【解析】
【分析】
(1)设购买A种树苗x棵,则购买B种树苗(100-x)棵,根据成活棵数=种植A种树苗的棵数×成活率+种植B种树苗的棵数×成活率,即可得出关于x的一元一次方程,解之即可得出结论;
(2)根据总费用=(A种树苗的单价+种植A种树苗的栽树劳务费)×种植A种树苗的棵数+(B种树苗的单价+种植B种树苗的栽树劳务费)×种植B种树苗的棵数,即可求出种植这片混合林的总费用.
(1)
解:设购买A种树苗x棵,则购买B种树苗(100-x)棵,
依题意,得:96%x+92%(100-x)=95,
解得:x=75,
100-x=25.
答:购买A种树苗75棵,购买B种树苗25棵;
(2)
解:(15+3)×75+(20+4)×(100-75)=1950(元).
答:种植这片混合林的总费用需1950元.
【点睛】
本题考查了一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)根据数量关系,列式计算.
5、 (1)2
(2)
(3)或
【解析】
【分析】
(1)由题意知,对应的数为,计算求解即可;
(2)分同向运动与相向运动两种情况讨论:当时, 对应的数分别为:,有,计算求解不合题意舍去;当时,对应的数分别为:有计算求符合要求的解即可;
(3)①MN与PQ相向运动时,N、P距离为3,N、P对应的数分别为:,,计算求解即可;②MN与PQ相向运动,相遇时,,解得,此时N、P对应的数均为0,Q、M对应的数分别为:1,;;③MN与PQ相向运动,2秒后开始重叠,重叠过程中速度减半,此过程中M、Q对应的数分别为:;当M、Q重合时,此时,解得,此时N、P对应的数分别为:;M、Q对应的数均为;;④MN与PQ反向运动,速度恢复,此时P、N对应的数分别为:,当P与A重合时,即,解得,此时N、P对应的数分别为:;M、Q对应的数分别为:;;⑤PQ开始沿数轴正向运动,速度不变,在M、Q重合时停止运动;此时M、Q对应的数分别为:;N、P对应的数分别为:;,解得,故可知在PQ沿数轴正向运动过程中不存在的情况;综上所述,可得到t的所有可能的值.
(1)
解: 数轴上两点A,B表示的数分别为﹣2,6,点C为点A、B的中点,
对应的数为:
故答案为:2
(2)
解:如图
∵
∴s
∵点在1秒后才可折返,
∴当时,对应的数分别为:
∴
∵
∴
解得:,不合题意故舍去;
当时,对应的数分别为:
∴
∵
∴
∴①,方程无解;或②,解得:
∴存在t使得成立,此时t的值为.
(3)
解:如图,①MN与PQ相向运动时,N、P距离为3,N、P对应的数分别为:,,解得;故时,;
②MN与PQ相向运动,相遇时,,解得,此时N、P对应的数均为0,Q 、M对应的数分别为:1,;
③MN与PQ相向运动,2秒后开始重叠,重叠过程中速度减半,此过程中M、Q对应的数分别为:;当M、Q重合时,此时,解得,此时N、P对应的数分别为:;M、Q对应的数均为;;
④MN与PQ反向运动,速度恢复,此时P、N对应的数分别为:,当P与A重合时,即,解得,此时N、P对应的数分别为:;M、Q对应的数分别为:;,故时,;
⑤PQ开始沿数轴正向运动,速度不变,在M、Q重合时停止运动;此时M、Q对应的数分别为:;N、P对应的数分别为:;,解得,故可知在PQ开始沿数轴正向运动过程中不存在的情况;
综上所述,存在t使两电子虫上的点N和点P刚好相距3个单位长度,t的值为.
【点睛】
本题考查的是数轴上中点对应的数,数轴上两点之间的距离,绝对值方程,一元一次方程的应用,解题的关键在于熟练的利用绝对值方程解决数轴上两点之间的距离问题.易错点是不能全面考虑运动的问题.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、若是关于的方程的解,则的值为( )
A.3 B.-3 C.1 D.-1
2、如果,那么下列等式不一定成立的是( )
A. B. C. D.
3、若a=b,m是任意实数,则下列等式不一定成立的是( )
A.a+m=b+m B.a﹣m=b﹣m C.am=bm D.
4、已知下列方程:①;②x+y;③x=0; ④x2+4x;⑤﹣3;⑥x(1﹣2x)=3x﹣1.其中是一元一次方程的是( )
A.①⑤ B.①③ C.①③⑥ D.⑤⑥
5、将正整数1至6000按一定规律排列如右表:同时平移表中带阴影的方框,方框中三个数的和可能是( )
A.116 B.117 C.129 D.138
6、已知a,x为正整数,若ax﹣1=x+7,则满足条件的所有a的值之和为( )
A.15 B.17 C.19 D.21
7、下列说法中,一定正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
8、幻方最早起源于中国,在《自然科学大事年表》中,对幻方做了特别的述说:“公元前一世纪,《大戴礼》记载,中国古代有象征吉祥的河图、洛书、纵横图,即为九宫算,被认为是现代组合数学最古老的发现”.请将,,,,,,,,分别填入如图所示的幻方中,要求同一横行、同一竖行以及同一条斜对角线上的3个数相加都得0,则x+y的值为( )
A. B. C. D.
9、已知是方程的解,则a的值是( )
A.36 B. C.4 D.
10、下列各式中,是一元一次方程的是( )
A.3x-5 B. C. D.5x-3y=0
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、若将数轴折叠,使得表示-1的点与表示5的点重合,则原点与表示_______的点重合.
2、某课外活动小组中女生人数占全组人数的一半,如果增加6名女生,那么女生人数就占全组人数的.设该课外活动小组共有x人,则可列方程为________.
3、五一期间,旅行社组织老师和学生共50人的旅行团去旅游,景区门票售价标准为:成人票50元/张,学生票20元/张,该旅行团购买门票共花费1900元,则该旅行团有老师 _____人.
4、已知点、在数轴上,点表示的数为-5,点表示的数为15.动点从点出发,以每秒3个单位长度的速度沿数轴正方向匀速移动,则点移动__________秒后,.
5、已知是方程的解,则a的值是______.
三、解答题(5小题,每小题10分,共计50分)
1、阅读理解:若、、为数轴上三点,若点到的距离是点到的距离的倍,即满足 时,则称点是“对的相关点”.例如,当点、、 表示的数分别为0,1,2时,,则称点是“对的2相关点”.
(1)如图1,点表示的数为,点表示的数为2.表示1的点到点的距离是2,到点的距离是1,那么点是“对的2相关点”;又如,表示0的点到点的距离是1,到点的距离是2,那么点 “对的2相关点”,但点 “对的2相关点”;(请在横线上填是或不是);
(2)如图2,、为数轴上两点,点所表示的数为,点所表示的数为4.在数轴上,数 所表示的点是“对的3相关点”;
(3)如图3,、为数轴上两点,点A所表示的数为,点B所表示的数为40.现有一只电子蚂蚁从点出发,以每秒4个单位的速度向左运动,到达点A停止.当经过多少秒时,、和中恰有一个点为“其余两点中一点对另一点的2相关点”?
2、解方程:
3、现有面值为5元和2元的人民币共32张,币值共计100元,问:这两种人民币各有多少张?
4、生态公园计划在园内的坡地上种植一片有A、B两种树的混合林,需要购买这两种树苗共100棵.假设这批树苗种植后成活95棵,种植A、B两种树苗的相关信息如下表:
品名 单价(元/棵) 栽树劳务费(元/棵) 成活率
A 15 3 96%
B 20 4 92%
(1)求购买A种和B种树苗各多少棵?
(2)求种植这片混合林的总费用需多少元?
5、如图,已知数轴上两点A,B表示的数分别为﹣2,6,用符号“”来表示点A和点B之间的距离.
(1)如图1,若点C为点A、B的中点,则点C表示的数为______;
(2)如图2,若点C对应数为4.点E以1个单位/秒的速度从点A出发沿着数轴的正方向运动,2秒后点F以2个单位/秒的速度从点C出发也沿着数轴的正方向运动,点F到达B点处立刻按原速返回沿着数轴的负方向运动,直到点E到达点B,两个点同时停止运动.设点E运动的时间为t(),在此过程中存在t使得成立,求t的值;
(3)如图3,若点C对应数为4.长度均为1个单位的电子虫MN和电子虫PQ,其中MN从点A出发(点N与点A重合)以1个单位/秒的速度沿着数轴的正方向运动,同时PQ从点C出发(点P与点C重合)以2个单位/秒的速度沿着数轴的负方向运动,当PQ运动到点P与点A重合时,PQ保持速度不变,反向沿着数轴正方向运动,当点Q运动到点M重合时,两电子虫都停止运动.在运动过程中,如果出现两条电子虫有重叠的时候,它们各自运动方向不变但速度会减半,重叠结束速度立即恢复.设电子虫MN运动时间为t秒,是否存在,使两电子虫上的点N和点P刚好相距3个单位长度,若存在,请直接写出t的值.若不存在,请说明理由.
-参考答案-
一、单选题
1、D
【解析】
【分析】
根据方程的解的定义,将代入方程得到关于的一元一次方程,解方程求解即可.
【详解】
解:∵是关于的方程的解,
∴
解得
故选D
【点睛】
本题考查了一元一次方程的解,解一元一次方程,掌握方程的解的定义是解题的关键.使方程左右两边的值相等的未知数的值是该方程的解.
2、D
【解析】
【分析】
根据等式的性质逐项分析即可.
【详解】
解:A. ∵,∴,故成立;
B. ∵,∴,故成立;
C. ∵,∴,故成立;
D. ∵,当m≠0时,,故不一定成立;
故选D.
【点睛】
本题考查了等式的基本性质,正确掌握等式的性质是解题的关键.等式的基本性质1是等式的两边都加上(或减去)同一个整式,所得的结果仍是等式;等式的基本性质2是等式的两边都乘以(或除以)同一个数(除数不能为0),所得的结果仍是等式.
3、D
【解析】
【分析】
根据等式的性质即可求出答案.
【详解】
解:A、利用等式性质1,两边都加m,得到a+m=b+m,原变形一定成立,故此选项不符合题意;
B、利用等式性质1,两边都减去m,得到a﹣m=b﹣m,原变形一定成立,故此选项不符合题意;
C、利用等式性质2,两边都乘m,得到am=bm,原变形一定成立,故此选项不符合题意;
D、成立的条件是m≠0,原变形不一定成立,故此选项符合题意;
故选:D.
【点睛】
本题考查了等式的性质,掌握等式的性质是解题的关键.等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数(或式子),结果仍相等.
4、B
【解析】
【分析】
由一元一次方程的概念可知:①含有一个未知数,②未知数的次数为1,③整式方程,据此进行判断即可.
【详解】
解::①是一元一次方程;
②x+y不是方程;
③x=0 是一元一次方程
④x2+4x不是方程;
⑤﹣3不是一元一次方程;
⑥x(1﹣2x)=3x﹣1,不是一元一次方程
故①③是一元一次方程,
故选B
【点睛】
本题考查了一元一次方程的概念,理解一元一次方程的概念是解题的关键.
5、A
【解析】
【分析】
设最左边数为x,则另外两个数分别为x+2、x+9,进而可得出三个数之和为3x+11,令其分别等于四个选项中数,解之即可得出x的值,由x为整数、x不能为第七列及第八列数,即可得到答案.
【详解】
解:设最左边数为x,则另外两个数分别为x+2、x+9,
∴三个数之和为x+x+2+x+9=3x+11.
根据题意得:3x+11=116,3x+11=117,3x+11=129,3x+11=138,
解得:x=35,x=(舍去),x=(舍去),x=(舍去),
故选:A.
【点睛】
本题考查了一元一次方程的应用以及规律型中数字的变化类,找准等量关系,正确列出一元一次方程是解题的关键.
6、C
【解析】
【分析】
移项,合并同类项,系数化为1,解原方程,根据x为正整数,得到几个关于a的一元一次方程,解之,求出a的值,相加求和即可得到答案.
【详解】
解:ax 1=x+7,
移项得:ax x=7+1,
合并同类项得:(a 1)x=8,
若a=1,则0=8,(无意义,舍去),
若a≠1,则x=,
∵x为正整数,
∴a 1=1或2或4或8,
解得:a=2或3或5或9,
∴a的值的和为:2+3+5+9=19,
故选C.
【点睛】
本题考查了一元一次方程的解,正确掌握解一元一次方程的方法是解题的关键.
7、A
【解析】
【分析】
根据等式两边同时乘以可对进行判断;利用等式两边同时除以c可对进行判断;利用平方根的定义对进行判断;根据等式的性质对进行判断.
【详解】
解:.若,则,所以选项符合题意;
.若,当时,,所以选项不符合题意;
.若,则或,所以选项不符合题意;
.若,则,所以选项不符合题意.
故选:.
【点睛】
本题考查了等式的性质:等式两边同时加上或减去同一个整式,等式仍然成立;等式两边同时乘或除以同一个不为0的整式,等式仍然成立.
8、B
【解析】
【分析】
设如图所示的幻方中y右边的方格中的数为z,根据“同一横行、同一竖行以及同一条斜对角线上的3个数相加都得0”可得,,,求出和的值,然后代入即可求出x+y的值.
【详解】
解:设如图所示的幻方中y右边的方格中的数为z,
∵同一横行、同一竖行以及同一条斜对角线上的3个数相加都得0,
∴,解得:,
又∵,将代入得:,
又∵,将代入得:,
∴.
故选:B.
【点睛】
此题考查了幻方的性质,代数式求值问题,解一元一次方程等知识,解题的关键是根据幻方中的规律列方程求出和的值.
9、A
【解析】
【分析】
把代入方程得到一个关于a的方程,从而求解.
【详解】
解:把代入方程,
得:,
解得:a=36,
故选:A.
【点睛】
本题考查了解一元一次方程以及方程的解的定义(方程两边左右相等的未知数的值叫做方程的解),理解定义是解题关键.
10、C
【解析】
【分析】
利用一元一次方程的定义进行解答即可.
【详解】
解:A、不是等式,所以不是一元一次方程,故此选项不合题意;
B、含有分式,不是一元一次方程,故此选项不合题意;
C、是一元一次方程,故此选项符合题意;
D、含有两个未知数,不是一元一次方程,故此选项不合题意;
故选:C.
【点睛】
此题主要考查了一元一次方程定义,关键是掌握一元一次方程属于整式方程,即方程两边都是整式.一元指方程仅含有一个未知数,一次指未知数的次数为1,且未知数的系数不为0.
二、填空题
1、4
【解析】
【分析】
设原点与表示x的点重合,先根据题意求出数轴上折叠的那个地方表示的数为,则,由此即可得到答案.
【详解】
解:设原点与表示x的点重合,
∵将数轴折叠,使得表示-1的点与表示5的点重合,
∴数轴上折叠的那个地方表示的数为,
∴,
解得,
故答案为:4.
【点睛】
本题主要考查了数轴上两点中点的计算方法,解一元一次方程,解题的关键在于能够根据题意求出折叠点表示的数.
2、
【解析】
【分析】
设小组原有人,则女生原有人,根据增加6名女生后就占全组的人数的,即可得出关于的一元一次方程,此题得解.
【详解】
解:设小组原有人,则女生原有人,
依题意得:.
故答案为:.
【点睛】
本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.
3、
【解析】
【分析】
设该旅行团有老师人,则有学生人,根据题意列一元一次方程解方程求解即可.
【详解】
解:设该旅行团有老师人,则有学生人,根据题意得,
解得
该旅行团有老师人
故答案为:
【点睛】
本题考查了一元一次方程的应用,根据题意列出方程是解题的关键.
4、5或10
【解析】
【分析】
分两种情况讨论,当点P在点B的左侧或点P在点B的右侧,再根据数轴上两点间的距离列方程解题.
【详解】
解:设t秒后,,此时点P表示的数为:-5+3t
分两种情况讨论,
①当点P在点B的左侧时,
;
②点P在点B的右侧,
综上所述,当或时,,
故答案为:5或10.
【点睛】
本题考查数轴上的动点问题、数轴上两点间的距离等知识,涉及一元一次方程,是重要考点,掌握相关知识是解题关键.
5、4
【解析】
【分析】
把代入方程得到关于的一元一次方程,依次去括号,移项,合并同类项,系数化为1,即可得到答案.
【详解】
解:把代入方程得:
,
去括号得:,
系数化为1得:,
故答案为:4.
【点睛】
本题考查了一元一次方程的解,解题的关键是正确掌握解一元一次方程的方法.
三、解答题
1、(1)不是,是;(2)或7;(3)5秒或7.5或10秒
【解析】
【分析】
(1)根据“A对B的2相关点”的定义和“B对A的2相关点”即可求解;
(2)根据“M对N的3相关点”的定义列方程即可求解;
(3)根据题意得:PB=4t,AB=40+20=60,PA=60-4t,由“A对B的2相关点”的定义可知:分两种情况列式:①PB=2PA;②PA=2PB;可以得出结论.
【详解】
解:(1)∵表示0的点D到点A的距离是1,到点B的距离是2,
那么点D不是“A对B的2相关点”,但点D是“B对A的2相关点”;
故答案为:不是,是;
(2)∵点M所表示的数为-2,点N所表示的数为4.设点C的坐标为x,
依题意得:,
解得:x=或7,
∴数或7所表示的点是“M对N的3相关点”;
故答案为:或7;
(3)由题意得:PB=4t,AB=40+20=60,PA=60-4t,
点P走完所用的时间为:60÷4=15(秒),
分四种情况:
①当PA=2PB时,即2×4t=60-4t,t=5(秒),P是“A对B的2相关点”,
②当PB=2PA时,即4t=2(60-4t),t=10(秒),P是“B对A的2相关点”,
③当AB=2PB时,即60=2×4t,t=7.5(秒),B是“A对P的2相关点”,
④当AB=2AP时,即60=2(60-4t),t=7.5(秒),A是“B对P的2相关点”,
∴当经过5秒或7.5或10秒时,P、A和B中恰有一个点为“其余两点中一点对另一点的2相关点”.
【点睛】
本题考查了数轴及数轴上两点的距离、动点问题,熟练掌握动点中三个量的数量关系式:路程=时间×速度,认真理解新定义是解题的关键.
2、
【解析】
【分析】
解一元一次方程,先去分母、去括号,然后移项合并同类项,最后系数化为1即可.
【详解】
解:去分母:
去括号:
移项:
合并同类项:
系数化为1:
∴是原方程的解.
【点睛】
本题考查了解一元一次方程.解题的关键在于去分母,去括号.
3、面值为5元得人民币由12张,面值为2元得人民币由20张.
【解析】
【分析】
设面值为5元得人民币由张,面值为2元得人民币由张,然后由面值共100元,列出方程,解方程即可.
【详解】
解答:解:设面值为5元得人民币由张,面值为2元得人民币由张,
根据题意得:,
解得:(张,
(张.
答:面值为5元得人民币由12张,面值为2元得人民币由20张.
【点睛】
此题属于一元一次方程的应用题,关键是由题意列出方程.
4、 (1)购买A种树苗75棵,购买B种树苗25棵;
(2)种植这片混合林的总费用需1950元.
【解析】
【分析】
(1)设购买A种树苗x棵,则购买B种树苗(100-x)棵,根据成活棵数=种植A种树苗的棵数×成活率+种植B种树苗的棵数×成活率,即可得出关于x的一元一次方程,解之即可得出结论;
(2)根据总费用=(A种树苗的单价+种植A种树苗的栽树劳务费)×种植A种树苗的棵数+(B种树苗的单价+种植B种树苗的栽树劳务费)×种植B种树苗的棵数,即可求出种植这片混合林的总费用.
(1)
解:设购买A种树苗x棵,则购买B种树苗(100-x)棵,
依题意,得:96%x+92%(100-x)=95,
解得:x=75,
100-x=25.
答:购买A种树苗75棵,购买B种树苗25棵;
(2)
解:(15+3)×75+(20+4)×(100-75)=1950(元).
答:种植这片混合林的总费用需1950元.
【点睛】
本题考查了一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)根据数量关系,列式计算.
5、 (1)2
(2)
(3)或
【解析】
【分析】
(1)由题意知,对应的数为,计算求解即可;
(2)分同向运动与相向运动两种情况讨论:当时, 对应的数分别为:,有,计算求解不合题意舍去;当时,对应的数分别为:有计算求符合要求的解即可;
(3)①MN与PQ相向运动时,N、P距离为3,N、P对应的数分别为:,,计算求解即可;②MN与PQ相向运动,相遇时,,解得,此时N、P对应的数均为0,Q、M对应的数分别为:1,;;③MN与PQ相向运动,2秒后开始重叠,重叠过程中速度减半,此过程中M、Q对应的数分别为:;当M、Q重合时,此时,解得,此时N、P对应的数分别为:;M、Q对应的数均为;;④MN与PQ反向运动,速度恢复,此时P、N对应的数分别为:,当P与A重合时,即,解得,此时N、P对应的数分别为:;M、Q对应的数分别为:;;⑤PQ开始沿数轴正向运动,速度不变,在M、Q重合时停止运动;此时M、Q对应的数分别为:;N、P对应的数分别为:;,解得,故可知在PQ沿数轴正向运动过程中不存在的情况;综上所述,可得到t的所有可能的值.
(1)
解: 数轴上两点A,B表示的数分别为﹣2,6,点C为点A、B的中点,
对应的数为:
故答案为:2
(2)
解:如图
∵
∴s
∵点在1秒后才可折返,
∴当时,对应的数分别为:
∴
∵
∴
解得:,不合题意故舍去;
当时,对应的数分别为:
∴
∵
∴
∴①,方程无解;或②,解得:
∴存在t使得成立,此时t的值为.
(3)
解:如图,①MN与PQ相向运动时,N、P距离为3,N、P对应的数分别为:,,解得;故时,;
②MN与PQ相向运动,相遇时,,解得,此时N、P对应的数均为0,Q 、M对应的数分别为:1,;
③MN与PQ相向运动,2秒后开始重叠,重叠过程中速度减半,此过程中M、Q对应的数分别为:;当M、Q重合时,此时,解得,此时N、P对应的数分别为:;M、Q对应的数均为;;
④MN与PQ反向运动,速度恢复,此时P、N对应的数分别为:,当P与A重合时,即,解得,此时N、P对应的数分别为:;M、Q对应的数分别为:;,故时,;
⑤PQ开始沿数轴正向运动,速度不变,在M、Q重合时停止运动;此时M、Q对应的数分别为:;N、P对应的数分别为:;,解得,故可知在PQ开始沿数轴正向运动过程中不存在的情况;
综上所述,存在t使两电子虫上的点N和点P刚好相距3个单位长度,t的值为.
【点睛】
本题考查的是数轴上中点对应的数,数轴上两点之间的距离,绝对值方程,一元一次方程的应用,解题的关键在于熟练的利用绝对值方程解决数轴上两点之间的距离问题.易错点是不能全面考虑运动的问题.
