华东师大版数学九年级下册27.2与圆有关的位置关系练习试题(Word版 含答案)
文档属性
| 名称 | 华东师大版数学九年级下册27.2与圆有关的位置关系练习试题(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 354.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 10:39:06 | ||
图片预览



文档简介
27.2与圆有关的位置关系练习试题
(限时70分钟 满分120分)
一、选择(本题共计7小题,每题5分,共计35分)
1.如图,△ABC是⊙O内接三角形,下列选项中,能使过点A的直线EF与⊙O相切于点A的条件是( )
A.∠EAB=∠C B.∠B=90° C.EF⊥AC D.AC是⊙O直径
2.PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=40°,则∠COD的度数是( )
A.50° B.60° C.70° D.75°
3.如图,四边形ABCD内接于圆O,AB为圆O的直径,CM切圆O于点C,∠BCM=60 ,则∠B的正切值是( )
A. B. C. D.
4.如图Rt△ABC中,∠ACB=90°,AC=4,AB=5,点P是AC上的一个动点(P不与点A、点C重合),PQ⊥AB,垂足为Q,当PQ与△ABC的内切圆⊙O相切时,PC的值为( )
A. B.1 C. D.
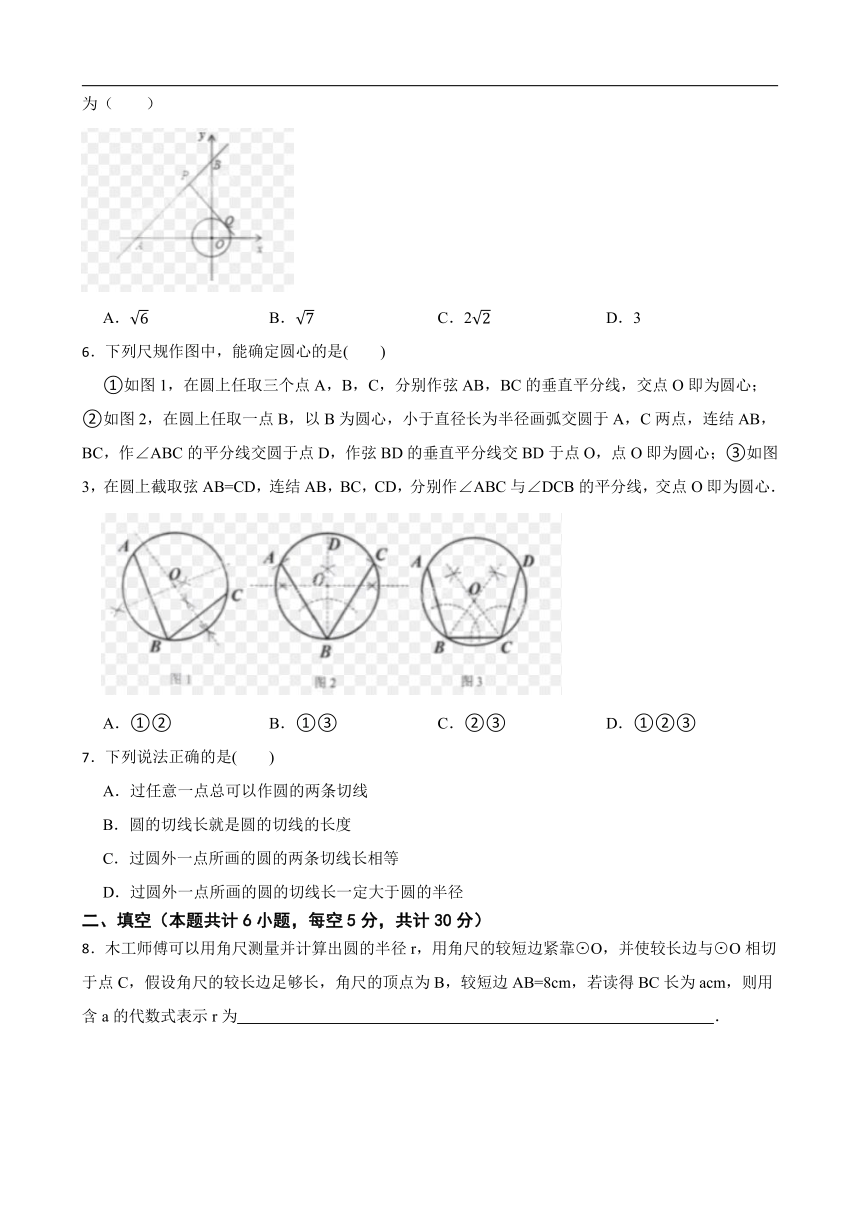
5.如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A. B. C.2 D.3
6.下列尺规作图中,能确定圆心的是( )
①如图1,在圆上任取三个点A,B,C,分别作弦AB,BC的垂直平分线,交点O即为圆心;②如图2,在圆上任取一点B,以B为圆心,小于直径长为半径画弧交圆于A,C两点,连结AB,BC,作∠ABC的平分线交圆于点D,作弦BD的垂直平分线交BD于点O,点O即为圆心;③如图3,在圆上截取弦AB=CD,连结AB,BC,CD,分别作∠ABC与∠DCB的平分线,交点O即为圆心.
A.①② B.①③ C.②③ D.①②③
7.下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
二、填空(本题共计6小题,每空5分,共计30分)
8.木工师傅可以用角尺测量并计算出圆的半径r,用角尺的较短边紧靠⊙O,并使较长边与⊙O相切于点C,假设角尺的较长边足够长,角尺的顶点为B,较短边AB=8cm,若读得BC长为acm,则用含a的代数式表示r为 .
9.平面直角坐标系内的三个点A(1,0)、B(0,-3)、C(2,-3) 确定一个圆(填“能”或“不能”)
10.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A= .
11.下列四个命题中,正确的是 (填写正确命题的序号)
①三角形的外心是三角形三边垂直平分线的交点;
②函数y=(1﹣a)x2﹣4x+6与x轴只有一个交点,则a=;
③半径分别为1和2的两圆相切,则两圆的圆心距为3;
④若对于任意x>1的实数,都有ax>1成立,则a的取值范围是a≥1.
12.如图, 是 的直径, 切 于点 ,线段 交 于点 .若 , ,则弧 的长为 .
13.如图,PA、PB是⊙O的切线,A、B为切点,点C、D在⊙O上.若∠P=108°,则∠B+∠D= .
三、解答(本题共计6小题,共55分)
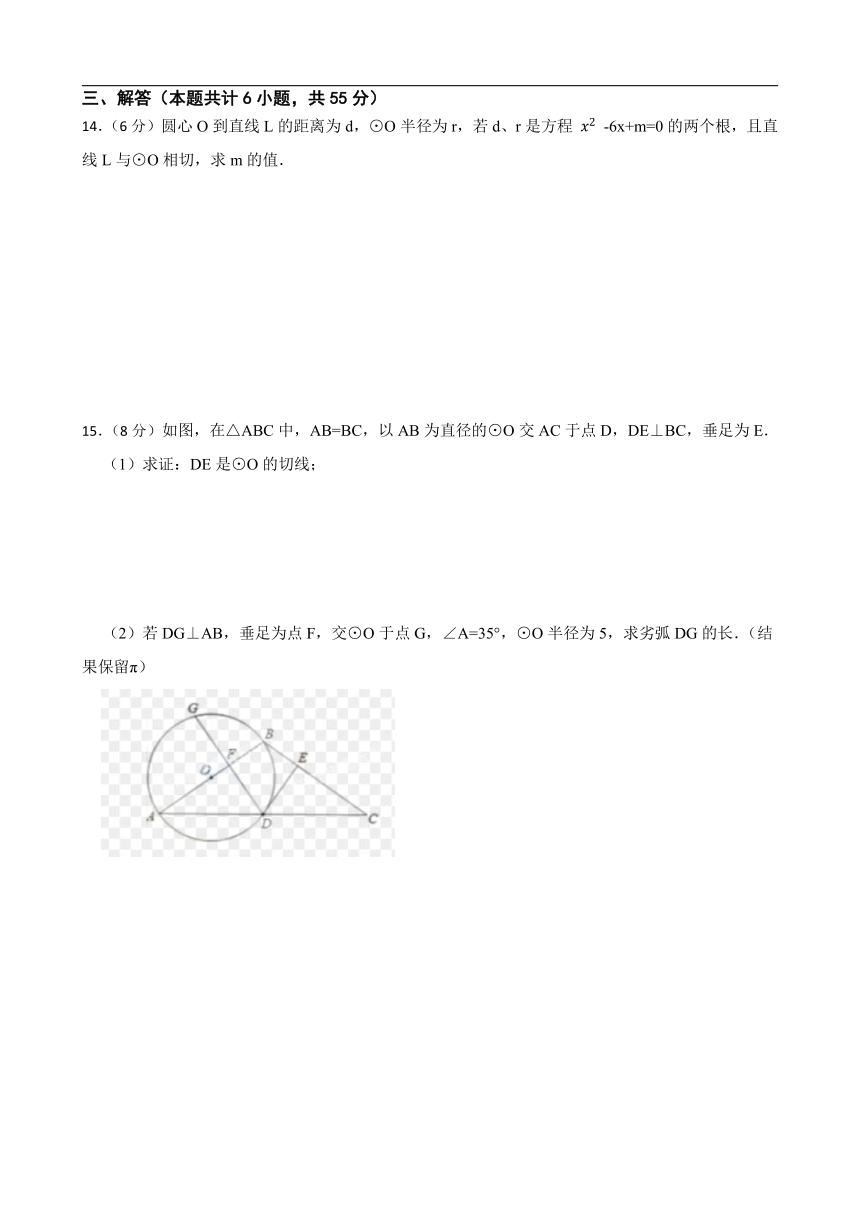
14.(6分)圆心O到直线L的距离为d,⊙O半径为r,若d、r是方程 -6x+m=0的两个根,且直线L与⊙O相切,求m的值.
15.(8分)如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,DE⊥BC,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若DG⊥AB,垂足为点F,交⊙O于点G,∠A=35°,⊙O半径为5,求劣弧DG的长.(结果保留π)
16.(10分)如图,⊙O经过点B、D、E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.
(1)试说明直线AC是⊙O的切线;
(2)当AE=4,AD=2时,求⊙O的半径及BC的长.
17.(10分)在 中, 为直径, 为 上一点.
(Ⅰ)如图①,过点 作 的切线,与 的延长线相交于点 ,若 ,求 的大小;
(Ⅱ)如图②, 为优弧 上一点,且 的延长线经过 的中点 ,连接 与 相交于点 ,若 ,求 的大小.
18.(10分)如图AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C作DC⊥OA,交AB于点D.
(1)求证:∠CDO=∠BDO;
(2)若∠A=30°,⊙O的半径为4,求阴影部分的面积(结果保留π).
19.(11分)如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,,C△ABC=10cm且∠C=60°.求:
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)
答案部分
1.A
2.C
3.D
4.C
5.B
6.A
7.C
8.r=8时,r=a;当r>8时,
9.能
10.76°
11.①④
12.
13.216°
14.解:∵d、r是方程x2-6x+m=0的两个根,且直线L与⊙O相切,
∴d=r,
∴方程有两个相等的实根,
∴△=36-4m=0,
解得,m=9.
15.(1)证明:如图1,连接BD、OD,
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=BC,
∴AD=DC,
∵AO=OB,
∴OD是△ABC的中位线,
∴DO∥BC,
∵DE⊥BC,
∴DE⊥OD,
∵OD为半径,
∴DE是⊙O切线;
(2)解:如图2所示,连接OG,OD
∵DG⊥AB,OB过圆心O,
∴弧BG=弧BD,
∵∠A=35°,
∴∠BOD=2∠A=70°,
∴∠BOG=∠BOD=70°,
∴∠GOD=140°,
∴劣弧DG的长是=π.
16.(1)证明:连接OE.
∵BE是∠ABC的平分线,
∴∠1=∠2.
∵OE=OB,
∴∠1=∠3.
∴∠2=∠3.
∴OE∥BC.
又∠C=90°,
∴∠AEO=90°.
∴AC是⊙O的切线.
(2)解:设⊙O的半径为r,在Rt△AEO中,由勾股定理可得OA2=OE2+AE2.
∵AE=4,AD=2,
∴(2+r)2=r2+42.
∴r=3.
∵OE∥BC,
∴.
∴.
∴BC=.
17.(Ⅰ)连接 ,如图①,
为切线,
,
,
,
,
,
;
(Ⅱ)如图②,
点 为 的中点,
,
,
,
,
.
18.(1)证明:AB切⊙O于点B,
∴OB⊥AB,即∠B=90°.
又∴DC⊥OA,∴∠OCD=90°.
在Rt△COD与Rt△BOD中,OD=OD,OB=OC,
∴Rt△COD≌Rt△BOD.
∴∠CDO=∠BDO.
(2)解:在Rt△ABO中,∠A=30°,OB=4,
∴∠BOC=60°,
∵Rt△COD≌Rt△BOD,
∴∠BOD=30°,
∴BD=OB·tan 30°=.
∴S四边形OCDB=2S△OBD=2××4×=.
∵∠BOC=60°,
∴S扇形OBC==.
∴S阴影=S四边形OCDB-S扇形OBC=-.
19.解:(1)连接OA,OB,OC,设⊙O的半径为r,∵S△ABC=S△AOB+S△AOC+S△BOC,∴S△ABC=AB r+BC r+AC r=(AB+BC+AC)r=C△ABC r,∵,C△ABC=10cm,∴r=2cm;(2)∵∠C=60°,∴∠EOF=120°,∴S扇形OEF==cm2;(3)∵∠C=60°,∴∠EOF=120°,∴C扇形OEF=l扇形OEF+2r=+2×2=+4(cm).
(限时70分钟 满分120分)
一、选择(本题共计7小题,每题5分,共计35分)
1.如图,△ABC是⊙O内接三角形,下列选项中,能使过点A的直线EF与⊙O相切于点A的条件是( )
A.∠EAB=∠C B.∠B=90° C.EF⊥AC D.AC是⊙O直径
2.PA,PB,CD是⊙O的切线,A,B,E是切点,CD分别交PA,PB于C,D两点,若∠APB=40°,则∠COD的度数是( )
A.50° B.60° C.70° D.75°
3.如图,四边形ABCD内接于圆O,AB为圆O的直径,CM切圆O于点C,∠BCM=60 ,则∠B的正切值是( )
A. B. C. D.
4.如图Rt△ABC中,∠ACB=90°,AC=4,AB=5,点P是AC上的一个动点(P不与点A、点C重合),PQ⊥AB,垂足为Q,当PQ与△ABC的内切圆⊙O相切时,PC的值为( )
A. B.1 C. D.
5.如图,在平面直角坐标系xOy中,直线AB经过点A(-4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
A. B. C.2 D.3
6.下列尺规作图中,能确定圆心的是( )
①如图1,在圆上任取三个点A,B,C,分别作弦AB,BC的垂直平分线,交点O即为圆心;②如图2,在圆上任取一点B,以B为圆心,小于直径长为半径画弧交圆于A,C两点,连结AB,BC,作∠ABC的平分线交圆于点D,作弦BD的垂直平分线交BD于点O,点O即为圆心;③如图3,在圆上截取弦AB=CD,连结AB,BC,CD,分别作∠ABC与∠DCB的平分线,交点O即为圆心.
A.①② B.①③ C.②③ D.①②③
7.下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
二、填空(本题共计6小题,每空5分,共计30分)
8.木工师傅可以用角尺测量并计算出圆的半径r,用角尺的较短边紧靠⊙O,并使较长边与⊙O相切于点C,假设角尺的较长边足够长,角尺的顶点为B,较短边AB=8cm,若读得BC长为acm,则用含a的代数式表示r为 .
9.平面直角坐标系内的三个点A(1,0)、B(0,-3)、C(2,-3) 确定一个圆(填“能”或“不能”)
10.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A= .
11.下列四个命题中,正确的是 (填写正确命题的序号)
①三角形的外心是三角形三边垂直平分线的交点;
②函数y=(1﹣a)x2﹣4x+6与x轴只有一个交点,则a=;
③半径分别为1和2的两圆相切,则两圆的圆心距为3;
④若对于任意x>1的实数,都有ax>1成立,则a的取值范围是a≥1.
12.如图, 是 的直径, 切 于点 ,线段 交 于点 .若 , ,则弧 的长为 .
13.如图,PA、PB是⊙O的切线,A、B为切点,点C、D在⊙O上.若∠P=108°,则∠B+∠D= .
三、解答(本题共计6小题,共55分)
14.(6分)圆心O到直线L的距离为d,⊙O半径为r,若d、r是方程 -6x+m=0的两个根,且直线L与⊙O相切,求m的值.
15.(8分)如图,在△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,DE⊥BC,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若DG⊥AB,垂足为点F,交⊙O于点G,∠A=35°,⊙O半径为5,求劣弧DG的长.(结果保留π)
16.(10分)如图,⊙O经过点B、D、E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.
(1)试说明直线AC是⊙O的切线;
(2)当AE=4,AD=2时,求⊙O的半径及BC的长.
17.(10分)在 中, 为直径, 为 上一点.
(Ⅰ)如图①,过点 作 的切线,与 的延长线相交于点 ,若 ,求 的大小;
(Ⅱ)如图②, 为优弧 上一点,且 的延长线经过 的中点 ,连接 与 相交于点 ,若 ,求 的大小.
18.(10分)如图AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C作DC⊥OA,交AB于点D.
(1)求证:∠CDO=∠BDO;
(2)若∠A=30°,⊙O的半径为4,求阴影部分的面积(结果保留π).
19.(11分)如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,,C△ABC=10cm且∠C=60°.求:
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)
答案部分
1.A
2.C
3.D
4.C
5.B
6.A
7.C
8.r=8时,r=a;当r>8时,
9.能
10.76°
11.①④
12.
13.216°
14.解:∵d、r是方程x2-6x+m=0的两个根,且直线L与⊙O相切,
∴d=r,
∴方程有两个相等的实根,
∴△=36-4m=0,
解得,m=9.
15.(1)证明:如图1,连接BD、OD,
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=BC,
∴AD=DC,
∵AO=OB,
∴OD是△ABC的中位线,
∴DO∥BC,
∵DE⊥BC,
∴DE⊥OD,
∵OD为半径,
∴DE是⊙O切线;
(2)解:如图2所示,连接OG,OD
∵DG⊥AB,OB过圆心O,
∴弧BG=弧BD,
∵∠A=35°,
∴∠BOD=2∠A=70°,
∴∠BOG=∠BOD=70°,
∴∠GOD=140°,
∴劣弧DG的长是=π.
16.(1)证明:连接OE.
∵BE是∠ABC的平分线,
∴∠1=∠2.
∵OE=OB,
∴∠1=∠3.
∴∠2=∠3.
∴OE∥BC.
又∠C=90°,
∴∠AEO=90°.
∴AC是⊙O的切线.
(2)解:设⊙O的半径为r,在Rt△AEO中,由勾股定理可得OA2=OE2+AE2.
∵AE=4,AD=2,
∴(2+r)2=r2+42.
∴r=3.
∵OE∥BC,
∴.
∴.
∴BC=.
17.(Ⅰ)连接 ,如图①,
为切线,
,
,
,
,
,
;
(Ⅱ)如图②,
点 为 的中点,
,
,
,
,
.
18.(1)证明:AB切⊙O于点B,
∴OB⊥AB,即∠B=90°.
又∴DC⊥OA,∴∠OCD=90°.
在Rt△COD与Rt△BOD中,OD=OD,OB=OC,
∴Rt△COD≌Rt△BOD.
∴∠CDO=∠BDO.
(2)解:在Rt△ABO中,∠A=30°,OB=4,
∴∠BOC=60°,
∵Rt△COD≌Rt△BOD,
∴∠BOD=30°,
∴BD=OB·tan 30°=.
∴S四边形OCDB=2S△OBD=2××4×=.
∵∠BOC=60°,
∴S扇形OBC==.
∴S阴影=S四边形OCDB-S扇形OBC=-.
19.解:(1)连接OA,OB,OC,设⊙O的半径为r,∵S△ABC=S△AOB+S△AOC+S△BOC,∴S△ABC=AB r+BC r+AC r=(AB+BC+AC)r=C△ABC r,∵,C△ABC=10cm,∴r=2cm;(2)∵∠C=60°,∴∠EOF=120°,∴S扇形OEF==cm2;(3)∵∠C=60°,∴∠EOF=120°,∴C扇形OEF=l扇形OEF+2r=+2×2=+4(cm).
