18.2.2 第2课时 菱形的判定 课件(23张PPT)
文档属性
| 名称 | 18.2.2 第2课时 菱形的判定 课件(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 15:13:15 | ||
图片预览






文档简介
(共23张PPT)
18.2.2 菱形
第2课时 菱 形 的 判 定
人教版 八年级下册 数学
(一)知识与技能: 理解并掌握菱形的三个判定方法,并会用三个判定方法进行相关的论证和计算。
(二)过程与方法: 经历探究菱形判定条件的过程,通过观察―猜想―证明―归纳―总结。发展自身合情推理能力,培养主动探究的习惯。
(三)情感态度与价值观: 在探究过程中,加深对菱形的理解,激发自己的求知欲望,进一步体会菱形的结构美和应用美。
学习目标
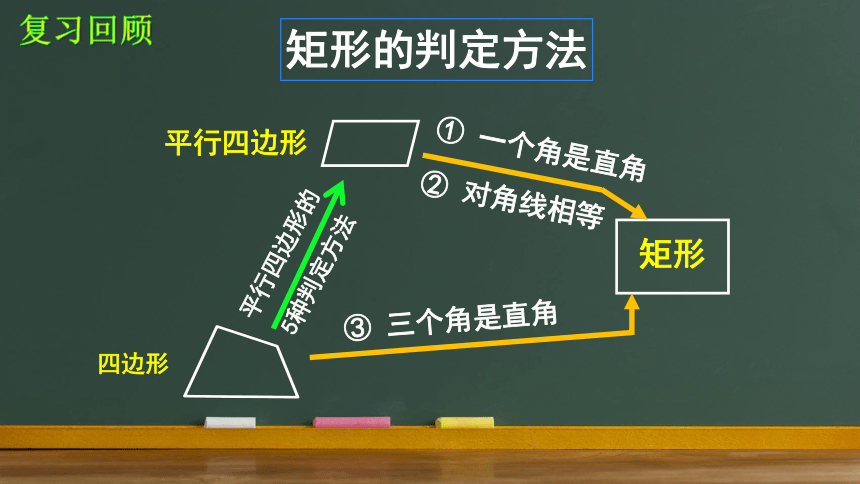
矩形的判定方法
矩形
平行四边形
① 一个角是直角
四边形
③ 三个角是直角
平行四边形的
5种判定方法
② 对角线相等
复习回顾
菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
∵ 四边形ABCD是平行四边形
A
B
C
D
且AB=BC
∴ 四边形ABCD是菱形.
几何语言:
(定义法)
复习回顾
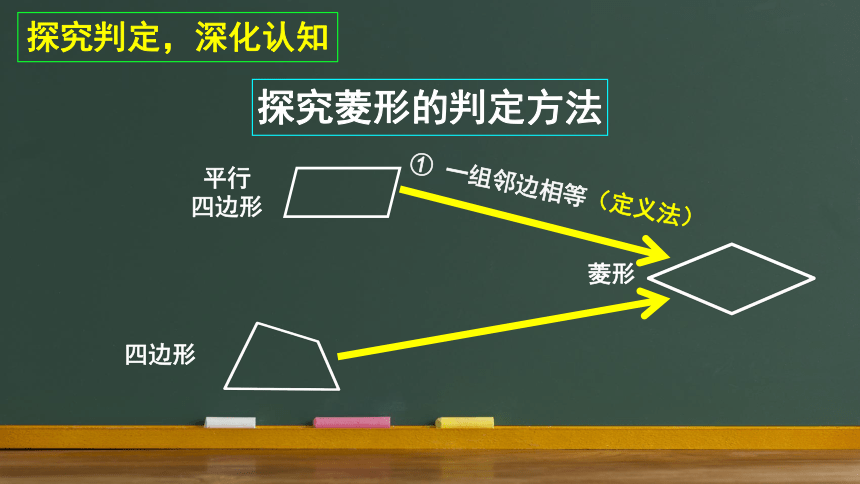
探究菱形的判定方法
四边形
平行
四边形
菱形
探究判定,深化认知
① 一组邻边相等(定义法)
前提条件是平行四边形
对角线互相垂直的平行四边形是菱形.
菱形的对角线互相垂直.
题设
结论
菱形的性质:
逆命题
猜想1 对角线互相垂直的平行四边形是菱形
已知:如图,在 ABCD中,对角线AC,
BD相交于点O,且AC⊥BD.
求证: ABCD是菱形.
A
B
D
C
O
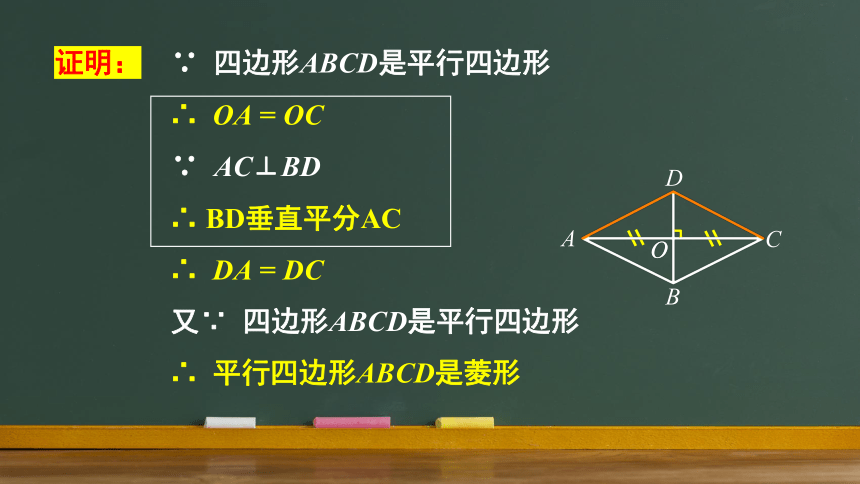
证明: ∵ 四边形ABCD是平行四边形
∴ OA = OC
∵ AC⊥BD
∴ BD垂直平分AC
∴ DA = DC
又∵ 四边形ABCD是平行四边形
∴ 平行四边形ABCD是菱形
A
B
D
O
C
O
菱形的判定定理:
对角线互相垂直的平行四边形是菱形.
A
B
D
C
O
在平行四边形ABCD中,
∵ AC⊥BD,
∴ 平行四边形ABCD是菱形.
结 论
几何语言:
菱形的四条边都相等.
四条边相等的四边形是菱形.
菱形的性质:
题设
结论
逆命题
猜想2 四条边相等的四边形是菱形
A
B
C
D
已知:如图,在四边形ABCD中,
AB = BC = CD = AD.
求证:四边形ABCD是菱形.
一组邻边相等 + 平行四边形
可用 AB = BC
AB = CD,BC = AD
A
B
C
D
证明:∵ AB = BC = CD = AD,
∴ AB = CD, BC = AD.
∴ 四边形ABCD是平行四边形.
又 AB = BC,
∴ 四边形ABCD是菱形.
菱形的判定定理:
四条边相等的四边形是菱形.
∵ AB = BC = CD = AD,
∴ 四边形ABCD是菱形.
A
B
C
D
结 论
几何语言:
菱形的判定方法:
(1)有一组邻边相等的平行四边形是菱形;
(2)对角线互相垂直的平行四边形是菱形;
(3)四条边相等的四边形是菱形。
应用练习,巩固知识
例 如图, ABCD的对角线AC,BD相交于点O,且AB = 5,AO = 4,BO = 3.
求证: ABCD是菱形.
A
B
C
D
O
A
B
O
3
4
5
AC⊥BD
ABCD
+
证明:
∵ 32+42=25,52=25
∴
∴ △AOB是直角三角形
∴ ∠AOB=90°
∴ AC⊥BD
又∵ ABCD是平行四边形
∴ ABCD是菱形
A
B
C
D
O
例 如图,AE∥BF,AC平分∠BAE,且交BF于点C,
BD平分∠ABC,且交AE于点D,连接CD.
求证:四边形ABCD是菱形.
2
1
3
A
D
E
O
B
C
F
教材P60 第6题
证明:∵ AE∥BF,
∴ ∠1 =∠2.
∵ AC平分∠BAD,
∴ ∠1 =∠3.
∴ ∠2 =∠3.
∴ AB = BC.
A
D
E
O
B
2
1
3
C
证明:同理 AB = AD.
∴ AD = BC.
∵ AD∥BC,
∴ 四边形ABCD是平行四边形.
又 AB = AD,
∴ 四边形ABCD是菱形.
A
D
E
O
B
2
1
3
C
方法总结:
方法1
方法2
方法3
一组邻边相等
对角线互相垂直
四条边相等
证明菱形
先证明平行四边形
四边形
平行四边形
+
平行四边形
+
菱形的判定
菱形
平行四边形
① 一组邻边相等
四边形
③ 四条边相等
平行四边形的
5种判定方法
② 对角线互相垂直
课堂小结
https://www.21cnjy.com/help/help_extract.php
18.2.2 菱形
第2课时 菱 形 的 判 定
人教版 八年级下册 数学
(一)知识与技能: 理解并掌握菱形的三个判定方法,并会用三个判定方法进行相关的论证和计算。
(二)过程与方法: 经历探究菱形判定条件的过程,通过观察―猜想―证明―归纳―总结。发展自身合情推理能力,培养主动探究的习惯。
(三)情感态度与价值观: 在探究过程中,加深对菱形的理解,激发自己的求知欲望,进一步体会菱形的结构美和应用美。
学习目标
矩形的判定方法
矩形
平行四边形
① 一个角是直角
四边形
③ 三个角是直角
平行四边形的
5种判定方法
② 对角线相等
复习回顾
菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
∵ 四边形ABCD是平行四边形
A
B
C
D
且AB=BC
∴ 四边形ABCD是菱形.
几何语言:
(定义法)
复习回顾
探究菱形的判定方法
四边形
平行
四边形
菱形
探究判定,深化认知
① 一组邻边相等(定义法)
前提条件是平行四边形
对角线互相垂直的平行四边形是菱形.
菱形的对角线互相垂直.
题设
结论
菱形的性质:
逆命题
猜想1 对角线互相垂直的平行四边形是菱形
已知:如图,在 ABCD中,对角线AC,
BD相交于点O,且AC⊥BD.
求证: ABCD是菱形.
A
B
D
C
O
证明: ∵ 四边形ABCD是平行四边形
∴ OA = OC
∵ AC⊥BD
∴ BD垂直平分AC
∴ DA = DC
又∵ 四边形ABCD是平行四边形
∴ 平行四边形ABCD是菱形
A
B
D
O
C
O
菱形的判定定理:
对角线互相垂直的平行四边形是菱形.
A
B
D
C
O
在平行四边形ABCD中,
∵ AC⊥BD,
∴ 平行四边形ABCD是菱形.
结 论
几何语言:
菱形的四条边都相等.
四条边相等的四边形是菱形.
菱形的性质:
题设
结论
逆命题
猜想2 四条边相等的四边形是菱形
A
B
C
D
已知:如图,在四边形ABCD中,
AB = BC = CD = AD.
求证:四边形ABCD是菱形.
一组邻边相等 + 平行四边形
可用 AB = BC
AB = CD,BC = AD
A
B
C
D
证明:∵ AB = BC = CD = AD,
∴ AB = CD, BC = AD.
∴ 四边形ABCD是平行四边形.
又 AB = BC,
∴ 四边形ABCD是菱形.
菱形的判定定理:
四条边相等的四边形是菱形.
∵ AB = BC = CD = AD,
∴ 四边形ABCD是菱形.
A
B
C
D
结 论
几何语言:
菱形的判定方法:
(1)有一组邻边相等的平行四边形是菱形;
(2)对角线互相垂直的平行四边形是菱形;
(3)四条边相等的四边形是菱形。
应用练习,巩固知识
例 如图, ABCD的对角线AC,BD相交于点O,且AB = 5,AO = 4,BO = 3.
求证: ABCD是菱形.
A
B
C
D
O
A
B
O
3
4
5
AC⊥BD
ABCD
+
证明:
∵ 32+42=25,52=25
∴
∴ △AOB是直角三角形
∴ ∠AOB=90°
∴ AC⊥BD
又∵ ABCD是平行四边形
∴ ABCD是菱形
A
B
C
D
O
例 如图,AE∥BF,AC平分∠BAE,且交BF于点C,
BD平分∠ABC,且交AE于点D,连接CD.
求证:四边形ABCD是菱形.
2
1
3
A
D
E
O
B
C
F
教材P60 第6题
证明:∵ AE∥BF,
∴ ∠1 =∠2.
∵ AC平分∠BAD,
∴ ∠1 =∠3.
∴ ∠2 =∠3.
∴ AB = BC.
A
D
E
O
B
2
1
3
C
证明:同理 AB = AD.
∴ AD = BC.
∵ AD∥BC,
∴ 四边形ABCD是平行四边形.
又 AB = AD,
∴ 四边形ABCD是菱形.
A
D
E
O
B
2
1
3
C
方法总结:
方法1
方法2
方法3
一组邻边相等
对角线互相垂直
四条边相等
证明菱形
先证明平行四边形
四边形
平行四边形
+
平行四边形
+
菱形的判定
菱形
平行四边形
① 一组邻边相等
四边形
③ 四条边相等
平行四边形的
5种判定方法
② 对角线互相垂直
课堂小结
https://www.21cnjy.com/help/help_extract.php
