山东省德州市2013届高三上学期期末校际联考 数学(文) Word版
文档属性
| 名称 | 山东省德州市2013届高三上学期期末校际联考 数学(文) Word版 |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-30 00:00:00 | ||
图片预览


文档简介
山东省德州市
2013届高三上学期期末校际联考
数学(文)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,测试时间120分钟.
注意事项:
1.答第Ⅰ卷前考生务必将自己的姓名、准考证号、考试科目用2B铅笔涂写在答题卡上.
2.选择题为四选一题目,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上,
第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共60分,把正确答案涂在答题卡上.
1.已知全集U={l,2,3,4,5,6},集合A={l,2.4:6},集合B={l,3,5},则( )
A.{l,2,3,4,5,6} B.{1,2,4,6} C.{2,4,6} D.{2,3,4,5,6}
2.已知复数z1,z2在复平面上对应的点分别为A(l,2),B(-1,3),则: ( )
A.1+i B.i C.1-i D.一i
3.设则“a≥1且b≥l”是“a+b≥2”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.不等式的解集为 ( )
A. B.C.D.
5.已知函数,则实数a的值等于 ( ) A.-3 B.-l C.1 D.-3或l
6.在各项均为正数的数列{an}中,对任意、都有·若则等于 ( )
A.216 B.510 C.512 D.l024
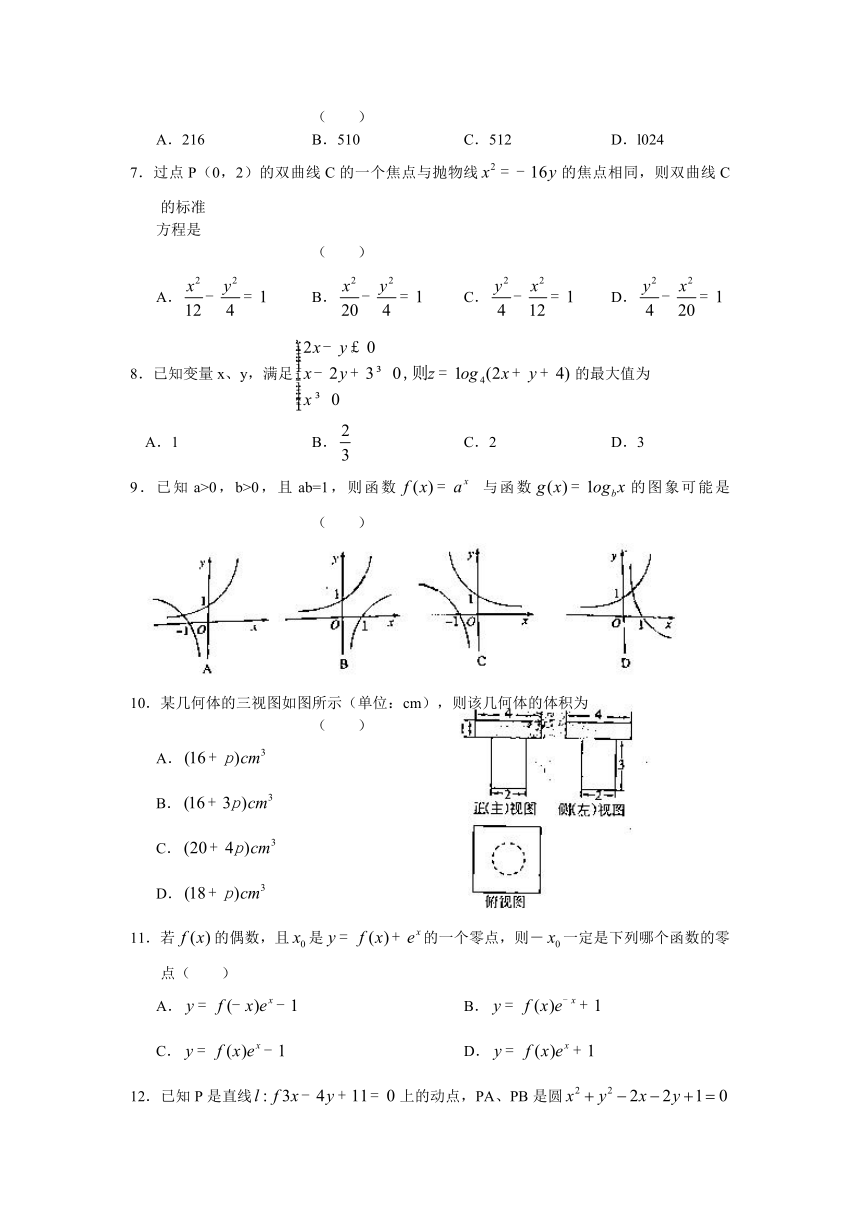
7.过点P(0,2)的双曲线C的一个焦点与抛物线的焦点相同,则双曲线C的标准
方程是 ( )
A. B. C. D.
8.已知变量x、y,满足的最大值为
A.1 B. C.2 D.3
9.已知a>0,b>0,且ab=1,则函数 与函数的图象可能是 ( )
10.某几何体的三视图如图所示(单位:cm),则该几何体的体积为 ( )
A.
B.
C.
D.
11.若的偶数,且是的一个零点,则-一定是下列哪个函数的零点( )
A. B.
C. D.
12.已知P是直线上的动点,PA、PB是圆的两条切
线,C是圆心,那么四边形PACB面积的最小值是 ( )
A. B.2 C. D.2
第II卷(共90分)
二、填空题:本大题共4小题,每小题4分.共16分.把答案填在答题纸的相应位置
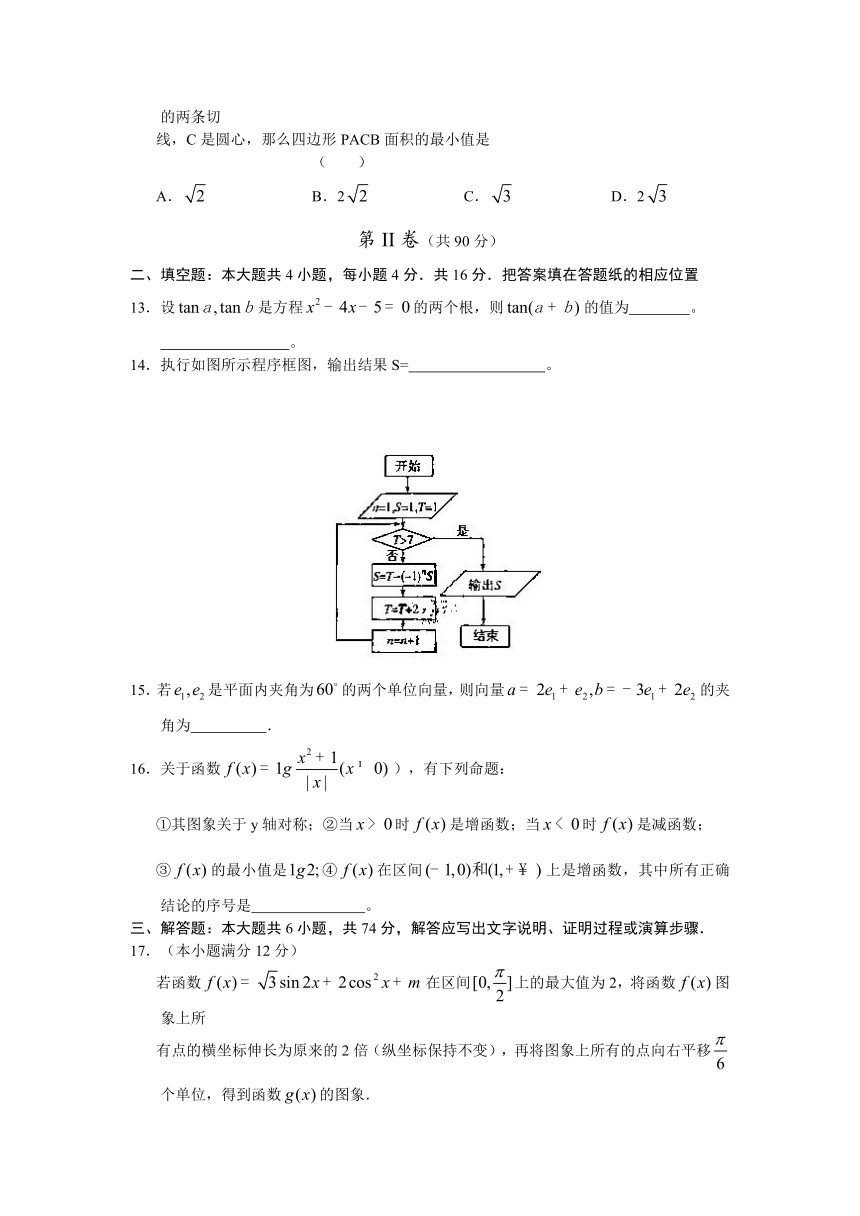
13.设是方程的两个根,则的值为 。
。
14.执行如图所示程序框图,输出结果S= 。
15.若是平面内夹角为的两个单位向量,则向量的夹角为 .
16.关于函数),有下列命题:
①其图象关于y轴对称;②当时是增函数;当时是减函数;
③的最小值是④在区间上是增函数,其中所有正确结论的序号是 。
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
若函数在区间上的最大值为2,将函数图象上所
有点的横坐标伸长为原来的2倍(纵坐标保持不变),再将图象上所有的点向右平移个单位,得到函数的图象.
(1)求函数解析式;
(2)在△ABC中,角A、B、C所对的边分别是a、b、c,又,△ABC的面
积等于3,求边长a的值,
18.(本小题满分l2分)
为了增强学生的环保意识,某中学随机抽取了50名学生举行了一次环保知识竞赛,本次竞赛的成绩(得分均为整数,满分100分)整理得到的频率分布直方图如下图。若图中第一组(成绩为[40,50))对应矩形高是第六组(成绩为[90,100])对应矩形高的一半.
(1)试求第一组、第六组分别有学生多少人?
(2)若从第一组中选出一名学生,从第六组中选
出2名学生,共3名学生召开座谈会,求第一组
中学生A1和第六组中学生B1同时被选中的概率.
19.(本小题满分12分)
已知数列{an}的公差为2的等差数列,它的前n项和为,且成等比数列.
(I)求{an}的通项公式;
(2)
20.(本小题满分12分)
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD= AB=1,
BC=,凸多面体ABCED的体积为,F为BC的中点.
(1)求证:AF∥平面BDE;
(2)求证:平面BDE⊥平面BCE.
21.(本小题满分12分)
设函数
(1)当a=l时,求曲线在点处的切线方程;
(2)若对恒成立,求实数a的取笸范围.
22.(本小题满分14分)
已知椭圆,焦点到短轴端点的距离为2,离心率为,过点
(m,o)作圆的切线交椭圆C于,A,B两点.
(1)求椭圆C的标准方程:
(2)将|AB|表示为m的函数,并求|AB|的最大值。
2013届高三上学期期末校际联考
数学(文)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,测试时间120分钟.
注意事项:
1.答第Ⅰ卷前考生务必将自己的姓名、准考证号、考试科目用2B铅笔涂写在答题卡上.
2.选择题为四选一题目,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上,
第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共60分,把正确答案涂在答题卡上.
1.已知全集U={l,2,3,4,5,6},集合A={l,2.4:6},集合B={l,3,5},则( )
A.{l,2,3,4,5,6} B.{1,2,4,6} C.{2,4,6} D.{2,3,4,5,6}
2.已知复数z1,z2在复平面上对应的点分别为A(l,2),B(-1,3),则: ( )
A.1+i B.i C.1-i D.一i
3.设则“a≥1且b≥l”是“a+b≥2”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.不等式的解集为 ( )
A. B.C.D.
5.已知函数,则实数a的值等于 ( ) A.-3 B.-l C.1 D.-3或l
6.在各项均为正数的数列{an}中,对任意、都有·若则等于 ( )
A.216 B.510 C.512 D.l024
7.过点P(0,2)的双曲线C的一个焦点与抛物线的焦点相同,则双曲线C的标准
方程是 ( )
A. B. C. D.
8.已知变量x、y,满足的最大值为
A.1 B. C.2 D.3
9.已知a>0,b>0,且ab=1,则函数 与函数的图象可能是 ( )
10.某几何体的三视图如图所示(单位:cm),则该几何体的体积为 ( )
A.
B.
C.
D.
11.若的偶数,且是的一个零点,则-一定是下列哪个函数的零点( )
A. B.
C. D.
12.已知P是直线上的动点,PA、PB是圆的两条切
线,C是圆心,那么四边形PACB面积的最小值是 ( )
A. B.2 C. D.2
第II卷(共90分)
二、填空题:本大题共4小题,每小题4分.共16分.把答案填在答题纸的相应位置
13.设是方程的两个根,则的值为 。
。
14.执行如图所示程序框图,输出结果S= 。
15.若是平面内夹角为的两个单位向量,则向量的夹角为 .
16.关于函数),有下列命题:
①其图象关于y轴对称;②当时是增函数;当时是减函数;
③的最小值是④在区间上是增函数,其中所有正确结论的序号是 。
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
若函数在区间上的最大值为2,将函数图象上所
有点的横坐标伸长为原来的2倍(纵坐标保持不变),再将图象上所有的点向右平移个单位,得到函数的图象.
(1)求函数解析式;
(2)在△ABC中,角A、B、C所对的边分别是a、b、c,又,△ABC的面
积等于3,求边长a的值,
18.(本小题满分l2分)
为了增强学生的环保意识,某中学随机抽取了50名学生举行了一次环保知识竞赛,本次竞赛的成绩(得分均为整数,满分100分)整理得到的频率分布直方图如下图。若图中第一组(成绩为[40,50))对应矩形高是第六组(成绩为[90,100])对应矩形高的一半.
(1)试求第一组、第六组分别有学生多少人?
(2)若从第一组中选出一名学生,从第六组中选
出2名学生,共3名学生召开座谈会,求第一组
中学生A1和第六组中学生B1同时被选中的概率.
19.(本小题满分12分)
已知数列{an}的公差为2的等差数列,它的前n项和为,且成等比数列.
(I)求{an}的通项公式;
(2)
20.(本小题满分12分)
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD= AB=1,
BC=,凸多面体ABCED的体积为,F为BC的中点.
(1)求证:AF∥平面BDE;
(2)求证:平面BDE⊥平面BCE.
21.(本小题满分12分)
设函数
(1)当a=l时,求曲线在点处的切线方程;
(2)若对恒成立,求实数a的取笸范围.
22.(本小题满分14分)
已知椭圆,焦点到短轴端点的距离为2,离心率为,过点
(m,o)作圆的切线交椭圆C于,A,B两点.
(1)求椭圆C的标准方程:
(2)将|AB|表示为m的函数,并求|AB|的最大值。
同课章节目录
