沪科版数学八年级下18.2勾股定理逆定理(第1课时)课件(共1张PPT)
文档属性
| 名称 | 沪科版数学八年级下18.2勾股定理逆定理(第1课时)课件(共1张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
沪科版 数学 八年级 下册
18.2 勾股定理的逆定理
第一课时
知识回顾
问题1:已学过直角三角形有哪些性质?
问题2:一个三角形满足什么条件是直角三角形
*直角三角形两锐角互余
*直角三角形斜边上中线等于斜边的一半
*勾股定理
直角三角形量直角边的平方和等于斜边的平方
*有一个角是直角 的三角形是直角三角形
还有别的判定方法吗?
新知导入
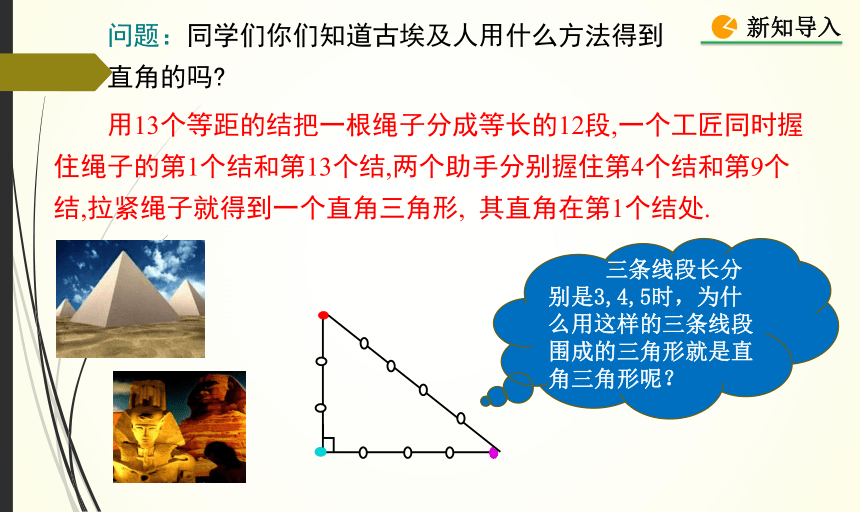
问题:同学们你们知道古埃及人用什么方法得到直角的吗
用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第9个结,拉紧绳子就得到一个直角三角形, 其直角在第1个结处.
三条线段长分别是3,4,5时,为什么用这样的三条线段围成的三角形就是直角三角形呢?
活动1、分别以下列三组数为边长画出三角形(单位:cm).
① 5,12,13; ② 7,24,25; ③ 8,15,17.
探究新知
活动2、用量角器量一量,它们都是直角三角形吗?
是直角三角形
①5,12,13; ②7,24,25; ③8,15,17.
讨论1:这三组数在数量关系上有什么相同点?
① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
③ 8,15,17满足82+152=172.
讨论2、古埃及人用来画直角的三边满足这个等式吗?
∵32+42=52,∴满足.
a2+b2=c2
探究新知
猜想:如果一个三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形
求证:
如果一个三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形
探究新知
命题证明步骤
(1)根据命题题设结论画图并结合图写已知求证
(2)分析题设结论,找出证明思路
(3)写出证明过程
A
B
C
a
b
c
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
△ABC≌ △ A′B′C′
?
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
构造两直角边分别为a,b的Rt△A′B′C′
探究新知
∠C= ∠C′ =90°
作一个直角∠MC1N,在C1M上截取C1B1=a=CB,在C1N上截C1A1=b=CA,
连接A1B1.
∴ △ABC ≌△A1B1C1 . (SSS)
∴ ∠C=∠C1=90°,
∴ △ABC是直角三角形.
a
c
b
A
C
B
b
a
C1
M
N
B1
A1
证明:
在Rt△A1C1B1中,由勾股定理,得A1B12=a2+b2=AB2 .
∴ A1B1=AB
在△ABC和△A1B1C 1中,
勾股定理的逆定理
A
C
B
a
b
c
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
直角三角形判定
题 设 结 论
勾股定理逆定理
三角形两边的平方和等于第三边的平方
这个三角形是直角三角形
一个三角形是直角三角形
直角三角形两直角边的平方和斜边的平方
勾股定理
例1、已知:△ABC的三边长为a=9cm,b=40cm,c=41cm,求三角形的面积
例题讲解
A
B
C
a
b
c
解:
如图所示
∵a=9cm,b=40cm
∴a2+b2=81+1600=1681
∵c=41
∴c =1681
∴ a2+b2=c
∴∠C=90°
S △ABC=×9×40=180(cm )
例2、已知a,b,c为△ABC的三边,且满足a c -b c =a4-b4,试判断此三角形的形状.
解:
∵a c -b c =a4-b4
∴(a -b )c =(a2+b2)(a2-b2)
∴(a -b )c -(a2+b2)(a2-b2)=0
∴(a -b )[c -(a2+b2)] =0
∴a -b =0 或 c -(a2+b2) =0
∴a=b 或 c =a2+b2
∴三角形为等腰三角形 或 三角形是直角三角形
随堂练习:
1、将下列长度的三木棒首尾顺次连接,能组成直角三角形的是( )
(A)1, 2, 3 (B)4, 6, 8 (C)5, 5, 4 (D)15,12, 9
2、如果线段a、b、c能组成直角三角形, 则它们的比可能是( )
(A)3:4:7; (B)5:12:13;
(C)1:2:4; (D)1:3:5.
D
B
三角形的三边分别是a、b、c, 且满足
(a+b)2-c2=2ab, 则此三角形是:( )
A. 直角三角形; B. 是锐角三角形;
是钝角三角形; D. 是等腰直角三角形.
A
4、已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
解:
由题意得:
AC=4
BC=3
AB=5
∵AB =25,BC +AC =25
∴AB =BC +AC
∴△ABC是直角三角形
B
2、一个零件的形状如下图所示,按规定这个零件
中∠A和∠DBC都应为直角,工人师傅量出这
个零件各边尺寸如下,那么这个零件符合要求吗?
A
B
C
D
3
4
5
12
13
巩固练习
解:
由题意得:
∵DB =25,AD +AB =25
∴DB =AB +AD
∴△ABD是直角三角形,且∠A=90°
∵DC =169,BC +BD =25+144=169
∴DC =BC +BD
∴△DBC是直角三角形且∠DBC=90°
∴这个零件符合要求
1.一个三角形三边分别是m -1,2m,m +1,则三角形中最大角是____度.
提升练习
解:
∵(m -1) =m4-2m +1
∵(m +1) =m4+2m +1
(2m) =4m2
∴(m -1) +(2m)
=m4-2m +1+4m2
=m4+2m +1
∴(m -1) +(2m) =(m +1)
∴三角形是直角三角形
90
提升练习
2、已知:点P是等边△ABC的内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转到△P’AB,求P’P的长及∠APB的度数
P
A
C
B
P’
解:
连结P’ P,由题意得: △P’AB≌ △PAC,
∴∠ P’AB= ∠PAC
P’A=PA, P’B= PC=10
∴∠ P’AB+∠BAP= ∠PAC +∠BAP
∴∠ P’AP= ∠BAC =60°
∴△ P’AP为等边三角形
∴P’P=PA=6, ∠P’PA=60°
∵P’P +PB =100=P’B ,
∴∠P’PB=90°
∴∠APB= ∠ P’AP+∠P’PB=90°+60°=150°
课堂小结
勾股定理的逆定理
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
注意:在运用勾股定理的逆定理时,先确定三边长,再找三边长的平方的关系,然后确定直角三角形(哪个角是直角).
直角三角形判定方法
沪科版 数学 八年级 下册
18.2 勾股定理的逆定理
第一课时
知识回顾
问题1:已学过直角三角形有哪些性质?
问题2:一个三角形满足什么条件是直角三角形
*直角三角形两锐角互余
*直角三角形斜边上中线等于斜边的一半
*勾股定理
直角三角形量直角边的平方和等于斜边的平方
*有一个角是直角 的三角形是直角三角形
还有别的判定方法吗?
新知导入
问题:同学们你们知道古埃及人用什么方法得到直角的吗
用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第9个结,拉紧绳子就得到一个直角三角形, 其直角在第1个结处.
三条线段长分别是3,4,5时,为什么用这样的三条线段围成的三角形就是直角三角形呢?
活动1、分别以下列三组数为边长画出三角形(单位:cm).
① 5,12,13; ② 7,24,25; ③ 8,15,17.
探究新知
活动2、用量角器量一量,它们都是直角三角形吗?
是直角三角形
①5,12,13; ②7,24,25; ③8,15,17.
讨论1:这三组数在数量关系上有什么相同点?
① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
③ 8,15,17满足82+152=172.
讨论2、古埃及人用来画直角的三边满足这个等式吗?
∵32+42=52,∴满足.
a2+b2=c2
探究新知
猜想:如果一个三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形
求证:
如果一个三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形
探究新知
命题证明步骤
(1)根据命题题设结论画图并结合图写已知求证
(2)分析题设结论,找出证明思路
(3)写出证明过程
A
B
C
a
b
c
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
△ABC≌ △ A′B′C′
?
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
构造两直角边分别为a,b的Rt△A′B′C′
探究新知
∠C= ∠C′ =90°
作一个直角∠MC1N,在C1M上截取C1B1=a=CB,在C1N上截C1A1=b=CA,
连接A1B1.
∴ △ABC ≌△A1B1C1 . (SSS)
∴ ∠C=∠C1=90°,
∴ △ABC是直角三角形.
a
c
b
A
C
B
b
a
C1
M
N
B1
A1
证明:
在Rt△A1C1B1中,由勾股定理,得A1B12=a2+b2=AB2 .
∴ A1B1=AB
在△ABC和△A1B1C 1中,
勾股定理的逆定理
A
C
B
a
b
c
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
直角三角形判定
题 设 结 论
勾股定理逆定理
三角形两边的平方和等于第三边的平方
这个三角形是直角三角形
一个三角形是直角三角形
直角三角形两直角边的平方和斜边的平方
勾股定理
例1、已知:△ABC的三边长为a=9cm,b=40cm,c=41cm,求三角形的面积
例题讲解
A
B
C
a
b
c
解:
如图所示
∵a=9cm,b=40cm
∴a2+b2=81+1600=1681
∵c=41
∴c =1681
∴ a2+b2=c
∴∠C=90°
S △ABC=×9×40=180(cm )
例2、已知a,b,c为△ABC的三边,且满足a c -b c =a4-b4,试判断此三角形的形状.
解:
∵a c -b c =a4-b4
∴(a -b )c =(a2+b2)(a2-b2)
∴(a -b )c -(a2+b2)(a2-b2)=0
∴(a -b )[c -(a2+b2)] =0
∴a -b =0 或 c -(a2+b2) =0
∴a=b 或 c =a2+b2
∴三角形为等腰三角形 或 三角形是直角三角形
随堂练习:
1、将下列长度的三木棒首尾顺次连接,能组成直角三角形的是( )
(A)1, 2, 3 (B)4, 6, 8 (C)5, 5, 4 (D)15,12, 9
2、如果线段a、b、c能组成直角三角形, 则它们的比可能是( )
(A)3:4:7; (B)5:12:13;
(C)1:2:4; (D)1:3:5.
D
B
三角形的三边分别是a、b、c, 且满足
(a+b)2-c2=2ab, 则此三角形是:( )
A. 直角三角形; B. 是锐角三角形;
是钝角三角形; D. 是等腰直角三角形.
A
4、已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
解:
由题意得:
AC=4
BC=3
AB=5
∵AB =25,BC +AC =25
∴AB =BC +AC
∴△ABC是直角三角形
B
2、一个零件的形状如下图所示,按规定这个零件
中∠A和∠DBC都应为直角,工人师傅量出这
个零件各边尺寸如下,那么这个零件符合要求吗?
A
B
C
D
3
4
5
12
13
巩固练习
解:
由题意得:
∵DB =25,AD +AB =25
∴DB =AB +AD
∴△ABD是直角三角形,且∠A=90°
∵DC =169,BC +BD =25+144=169
∴DC =BC +BD
∴△DBC是直角三角形且∠DBC=90°
∴这个零件符合要求
1.一个三角形三边分别是m -1,2m,m +1,则三角形中最大角是____度.
提升练习
解:
∵(m -1) =m4-2m +1
∵(m +1) =m4+2m +1
(2m) =4m2
∴(m -1) +(2m)
=m4-2m +1+4m2
=m4+2m +1
∴(m -1) +(2m) =(m +1)
∴三角形是直角三角形
90
提升练习
2、已知:点P是等边△ABC的内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转到△P’AB,求P’P的长及∠APB的度数
P
A
C
B
P’
解:
连结P’ P,由题意得: △P’AB≌ △PAC,
∴∠ P’AB= ∠PAC
P’A=PA, P’B= PC=10
∴∠ P’AB+∠BAP= ∠PAC +∠BAP
∴∠ P’AP= ∠BAC =60°
∴△ P’AP为等边三角形
∴P’P=PA=6, ∠P’PA=60°
∵P’P +PB =100=P’B ,
∴∠P’PB=90°
∴∠APB= ∠ P’AP+∠P’PB=90°+60°=150°
课堂小结
勾股定理的逆定理
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
注意:在运用勾股定理的逆定理时,先确定三边长,再找三边长的平方的关系,然后确定直角三角形(哪个角是直角).
直角三角形判定方法
