人教版数学七年级下册 6.3 第12课时平方根(二) 课件(共22张PPT)
文档属性
| 名称 | 人教版数学七年级下册 6.3 第12课时平方根(二) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 11:23:41 | ||
图片预览





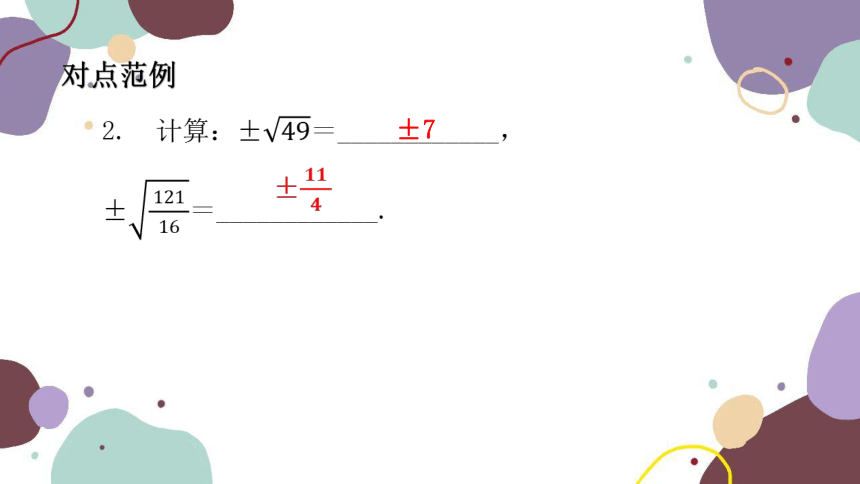

文档简介
(共22张PPT)
第六章 实数
第12课时 平方根(二)
目录
01
本课目标
02
课堂演练
1. 了解平方根的定义和性质.
2. 了解乘方与开方互为逆运算,能依据平方运算求百以内正整数的平方根,并会用符号表示.
一般地,如果一个数的____________等于a,那么这个数叫做a的平方根或二次方根,记作____________.
知识重点
知识点一 平方根的定义
平方
1. 若一个数的平方等于4,则这个数等于( )
A. ±2 B. 2
C. ±16 D. 16
对点范例
A
求一个数a的____________的运算,叫做开平方.
知识重点
知识点二 开平方的定义
平方根
对点范例
±7
正数有____________个平方根,它们互为相反数;0的平方根是____________;____________数没有平方根.
知识重点
知识点三 平方根的性质
两
0
负
对点范例
D
先将方程化为x2=a或(x-b)2=a的形式,再利用_______________的定义和整体思想求解.
知识重点
知识点四 解方程
平方根
4. 若x2=9,则x的取值是( )
A.x=3 B.x=-3
C.x=±3 D.x=±4.5
对点范例
C
【例1】81的平方根是( )
A.81 B.9
C.-9 D.±9
思路点拨:一个正数的平方根有两个,它们互为相反数,其中正值为算术平方根.
典型例题
D
5. (-0.7)2的平方根是( )
A. -0.7 B. 0.7
C. ±0.7 D. 0.49
举一反三
C
典型例题
解:(1)9的平方根为±3.
(3)0.01的平方根为±0.1.
举一反三
解:(1)4 900的平方根是±70.
(4)0.001 6的平方根是±0.04.
典型例题
举一反三
【例4】一个正数的两个平方根是a+6与2a-9,求这
个正数.
思路点拨:根据平方根的性质正确求出a的值是解题的关键.
典型例题
解:由题意,得a+6+2a-9=0. 解得a=1.
∴这个正数是(a+6)2=72=49.
8. 已知一个正数x的平方根是2a-3与5-a,求正数x.
举一反三
解:由题意,得2a-3+5-a=0.
解得a=-2.
∴2a-3=-7.
∴x=49.
【例5】已知2(x-2)2=8,求x的值.
思路点拨:把方程化为(x-2)2=4,再根据平方根的定义解答即可.
典型例题
解:整理方程,得(x-2)2=4.
开方,得x-2=2或x-2=-2.
解得x=4或x=0.
9. 求下列方程中x的值:
(1)4x2=121;(2)(x+2)2=25.
举一反三
(2)开方,得x+2=5或x+2=-5.
解得x=3或x=-7.
谢 谢
第六章 实数
第12课时 平方根(二)
目录
01
本课目标
02
课堂演练
1. 了解平方根的定义和性质.
2. 了解乘方与开方互为逆运算,能依据平方运算求百以内正整数的平方根,并会用符号表示.
一般地,如果一个数的____________等于a,那么这个数叫做a的平方根或二次方根,记作____________.
知识重点
知识点一 平方根的定义
平方
1. 若一个数的平方等于4,则这个数等于( )
A. ±2 B. 2
C. ±16 D. 16
对点范例
A
求一个数a的____________的运算,叫做开平方.
知识重点
知识点二 开平方的定义
平方根
对点范例
±7
正数有____________个平方根,它们互为相反数;0的平方根是____________;____________数没有平方根.
知识重点
知识点三 平方根的性质
两
0
负
对点范例
D
先将方程化为x2=a或(x-b)2=a的形式,再利用_______________的定义和整体思想求解.
知识重点
知识点四 解方程
平方根
4. 若x2=9,则x的取值是( )
A.x=3 B.x=-3
C.x=±3 D.x=±4.5
对点范例
C
【例1】81的平方根是( )
A.81 B.9
C.-9 D.±9
思路点拨:一个正数的平方根有两个,它们互为相反数,其中正值为算术平方根.
典型例题
D
5. (-0.7)2的平方根是( )
A. -0.7 B. 0.7
C. ±0.7 D. 0.49
举一反三
C
典型例题
解:(1)9的平方根为±3.
(3)0.01的平方根为±0.1.
举一反三
解:(1)4 900的平方根是±70.
(4)0.001 6的平方根是±0.04.
典型例题
举一反三
【例4】一个正数的两个平方根是a+6与2a-9,求这
个正数.
思路点拨:根据平方根的性质正确求出a的值是解题的关键.
典型例题
解:由题意,得a+6+2a-9=0. 解得a=1.
∴这个正数是(a+6)2=72=49.
8. 已知一个正数x的平方根是2a-3与5-a,求正数x.
举一反三
解:由题意,得2a-3+5-a=0.
解得a=-2.
∴2a-3=-7.
∴x=49.
【例5】已知2(x-2)2=8,求x的值.
思路点拨:把方程化为(x-2)2=4,再根据平方根的定义解答即可.
典型例题
解:整理方程,得(x-2)2=4.
开方,得x-2=2或x-2=-2.
解得x=4或x=0.
9. 求下列方程中x的值:
(1)4x2=121;(2)(x+2)2=25.
举一反三
(2)开方,得x+2=5或x+2=-5.
解得x=3或x=-7.
谢 谢
