人教版数学七年级下册 5.11 第10课时平移 课件(共19张PPT)
文档属性
| 名称 | 人教版数学七年级下册 5.11 第10课时平移 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
第五章 相交线与平行线
第10课时 平移
目录
01
本课目标
02
课堂演练
1. 了解平移的概念,理解平移前后的图形对应点所连的线段平行(或在同一条直线上)且相等的性质.
2. 能按要求作出简单平面图形平移后的图形.
3. 能利用平移进行简单的图案设计,认识和欣赏平移在生活中的应用,培养观察和动手操作的能力.
把一个图形整体沿____________________移动,会得到一个新图形,图形的这种移动叫做平移.平移的两个要素是:平移的____________与平移的____________.
知识重点
知识点一 平移的定义
某一直线方向
方向
距离
1. 下列生活现象中,属于平移的是( )
A.足球在草地上滚动
B.急刹车时汽车在地面上滑行
C.投影片的文字经投影转换到屏幕上
D.钟摆的摆动
对点范例
B
(1)平移前后的图形形状和大小完全____________;
(2)连接各组对应点的线段____________(或在同一条直线上)且相等.
知识重点
知识点二 平移的性质
相同
平行
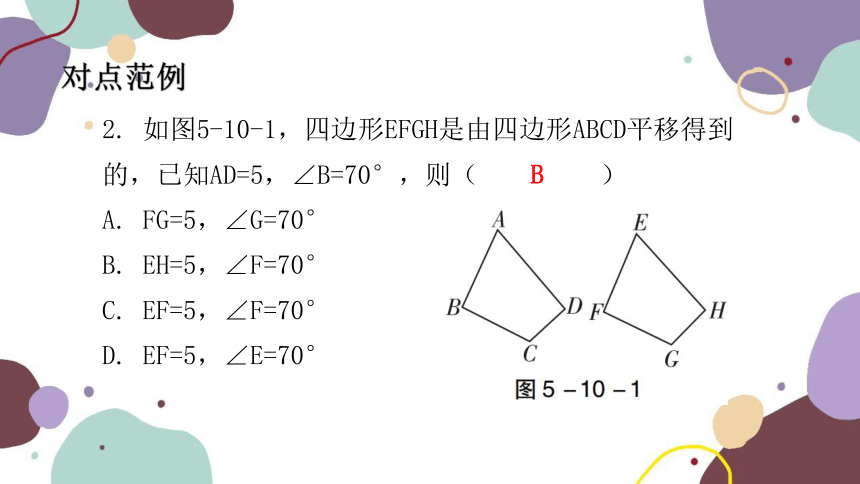
2. 如图5-10-1,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A. FG=5,∠G=70°
B. EH=5,∠F=70°
C. EF=5,∠F=70°
D. EF=5,∠E=70°
对点范例
B
一找:找出平移的____________;
二定:确定表示图形的__________________;
三移:过关键点作____________________的线段,得到关键点的对应点;
四连:按原图形的顺序连接关键点的对应点.
知识重点
知识点三 平移作图
方向
关键点
平行且相等
3. 过点D作三角形ABC平移后的图形,请填空:
(1)连接____________,
(2)作____________∥AD且____________=AD,
(3)作____________∥AD且____________=AD,
(4)顺次连接D,E,F,得到三角形ABC平移后的图形三角形DEF.
对点范例
AD
BE
BE
CF
CF
【例1】下面选项中的四个小船,可由图5-10-3平移得到的是( )
思路点拨:掌握图形的平移只改变图形的位置,而不改变图形的形状和大小.
典型例题
C
4. 在下面选项中的四个图,能由图5-10-4经过平移得到的是( )
举一反三
D
【例2】如图5-10-5,三角形ABC沿直线m向右平移a cm,得到三角形DEF.下列说法错误的是( )
A. AC∥DF B. CF∥AB
C. CF=a cm D. DE=a cm
思路点拨:图形经过平移后,连接各组对应点的线段平行(或在同一条直线上)且相等.
典型例题
D
5. 如图5-10-6,把直角三角形ABC(∠ABC=90°)沿着射线BC方向平移得到直角三角形DEF,若AB=8,BE=5,则四边形ACFD的面积是____________.
举一反三
40
【例3】(创新题)如图5-10-7,将长为6 cm,宽为4 cm的长方形ABCD先向右平移2 cm,再向下平移1 cm,得到长方形A′B′C′D′,则阴影部分的面积为____________ cm2.
思路点拨:利用平移的性质求出空白部分矩形的长,宽即可解决问题.
典型例题
24
6. (创新题)如图5-10-8是一块白色正方形布,边长是1.8 m,上面横竖各有两道黑条,黑条的宽是0.2 m,利用平移知识得白色部分的面积是____________m2.
举一反三
1.96
【例4】如图5-10-9,假设三角形ABC平移后的图形是三角形A′B′C′,其中C与C′是对应点,请画出平移后的三角形A′B′C′.
典型例题
解:如答图5-10-1,三角形A′B′C′就是所要画的三角形.
思路点拨:确定平移后图形的基本要素有两个,即平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
7. 在如图5-10-10所示的网格中,将三角形ABC向右平移4格,再向下平移2格.
(1)请你画出经过两次平移后的三角形DEF(点A与点D,点B与点E,点C与点F对应);
举一反三
解:(1)如答图5-10-2,三角形DEF即为所求.
(2)若网格每个小正方形的边长为1个单位长度,连接BE和CE,请求出三角形BCE的面积.
谢 谢
第五章 相交线与平行线
第10课时 平移
目录
01
本课目标
02
课堂演练
1. 了解平移的概念,理解平移前后的图形对应点所连的线段平行(或在同一条直线上)且相等的性质.
2. 能按要求作出简单平面图形平移后的图形.
3. 能利用平移进行简单的图案设计,认识和欣赏平移在生活中的应用,培养观察和动手操作的能力.
把一个图形整体沿____________________移动,会得到一个新图形,图形的这种移动叫做平移.平移的两个要素是:平移的____________与平移的____________.
知识重点
知识点一 平移的定义
某一直线方向
方向
距离
1. 下列生活现象中,属于平移的是( )
A.足球在草地上滚动
B.急刹车时汽车在地面上滑行
C.投影片的文字经投影转换到屏幕上
D.钟摆的摆动
对点范例
B
(1)平移前后的图形形状和大小完全____________;
(2)连接各组对应点的线段____________(或在同一条直线上)且相等.
知识重点
知识点二 平移的性质
相同
平行
2. 如图5-10-1,四边形EFGH是由四边形ABCD平移得到的,已知AD=5,∠B=70°,则( )
A. FG=5,∠G=70°
B. EH=5,∠F=70°
C. EF=5,∠F=70°
D. EF=5,∠E=70°
对点范例
B
一找:找出平移的____________;
二定:确定表示图形的__________________;
三移:过关键点作____________________的线段,得到关键点的对应点;
四连:按原图形的顺序连接关键点的对应点.
知识重点
知识点三 平移作图
方向
关键点
平行且相等
3. 过点D作三角形ABC平移后的图形,请填空:
(1)连接____________,
(2)作____________∥AD且____________=AD,
(3)作____________∥AD且____________=AD,
(4)顺次连接D,E,F,得到三角形ABC平移后的图形三角形DEF.
对点范例
AD
BE
BE
CF
CF
【例1】下面选项中的四个小船,可由图5-10-3平移得到的是( )
思路点拨:掌握图形的平移只改变图形的位置,而不改变图形的形状和大小.
典型例题
C
4. 在下面选项中的四个图,能由图5-10-4经过平移得到的是( )
举一反三
D
【例2】如图5-10-5,三角形ABC沿直线m向右平移a cm,得到三角形DEF.下列说法错误的是( )
A. AC∥DF B. CF∥AB
C. CF=a cm D. DE=a cm
思路点拨:图形经过平移后,连接各组对应点的线段平行(或在同一条直线上)且相等.
典型例题
D
5. 如图5-10-6,把直角三角形ABC(∠ABC=90°)沿着射线BC方向平移得到直角三角形DEF,若AB=8,BE=5,则四边形ACFD的面积是____________.
举一反三
40
【例3】(创新题)如图5-10-7,将长为6 cm,宽为4 cm的长方形ABCD先向右平移2 cm,再向下平移1 cm,得到长方形A′B′C′D′,则阴影部分的面积为____________ cm2.
思路点拨:利用平移的性质求出空白部分矩形的长,宽即可解决问题.
典型例题
24
6. (创新题)如图5-10-8是一块白色正方形布,边长是1.8 m,上面横竖各有两道黑条,黑条的宽是0.2 m,利用平移知识得白色部分的面积是____________m2.
举一反三
1.96
【例4】如图5-10-9,假设三角形ABC平移后的图形是三角形A′B′C′,其中C与C′是对应点,请画出平移后的三角形A′B′C′.
典型例题
解:如答图5-10-1,三角形A′B′C′就是所要画的三角形.
思路点拨:确定平移后图形的基本要素有两个,即平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
7. 在如图5-10-10所示的网格中,将三角形ABC向右平移4格,再向下平移2格.
(1)请你画出经过两次平移后的三角形DEF(点A与点D,点B与点E,点C与点F对应);
举一反三
解:(1)如答图5-10-2,三角形DEF即为所求.
(2)若网格每个小正方形的边长为1个单位长度,连接BE和CE,请求出三角形BCE的面积.
谢 谢
