28.1 锐角三角函数(1)--正弦
文档属性
| 名称 | 28.1 锐角三角函数(1)--正弦 |  | |
| 格式 | zip | ||
| 文件大小 | 206.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-31 11:26:35 | ||
图片预览


文档简介
课件26张PPT。只有不断的思考,才会有新的发现;
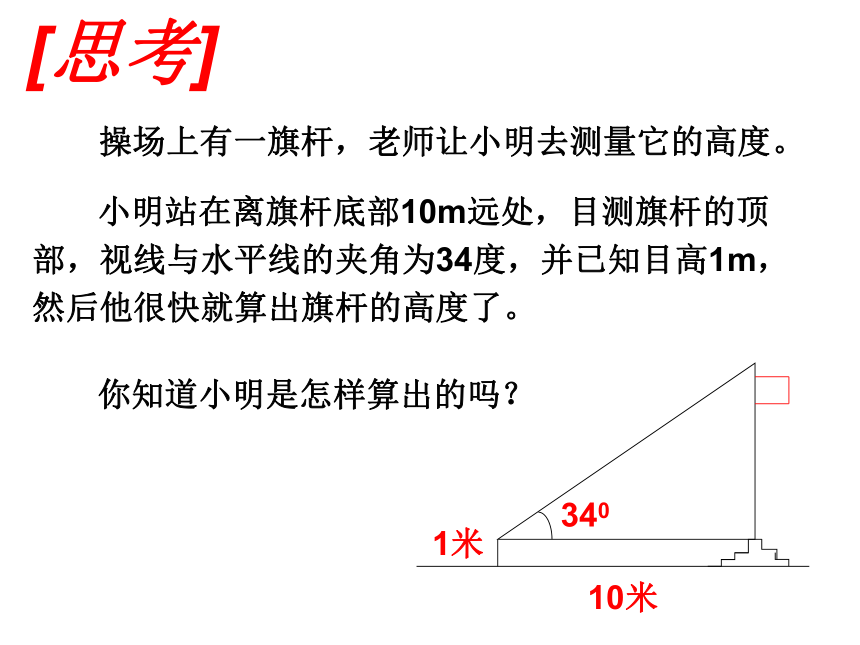
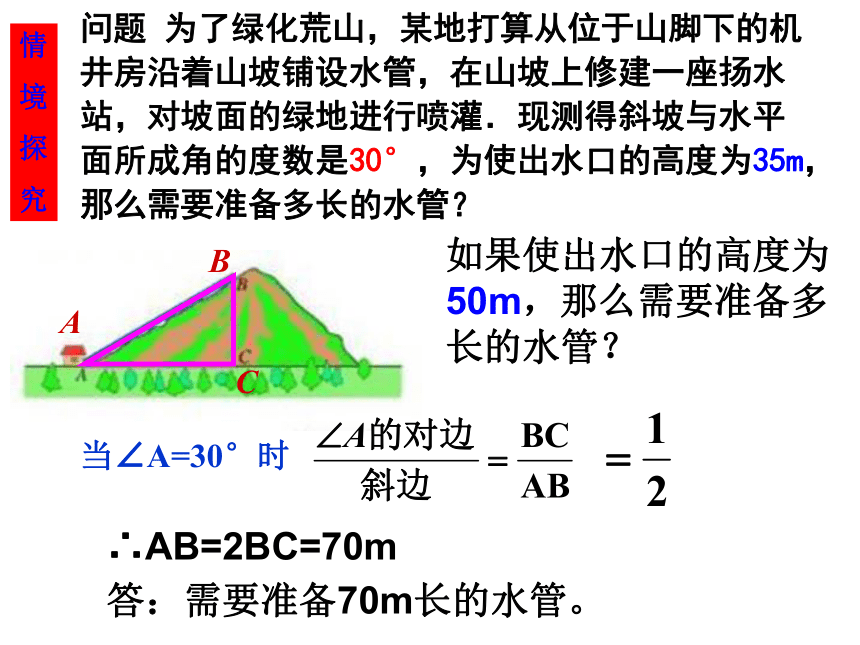
只有量的变化,才会有质的进步。[思考] 操场上有一旗杆,老师让小明去测量它的高度。 小明站在离旗杆底部10m远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高1m,然后他很快就算出旗杆的高度了。 你知道小明是怎样算出的吗?3401米10米28.1 锐角三角函数(1)——正 弦问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
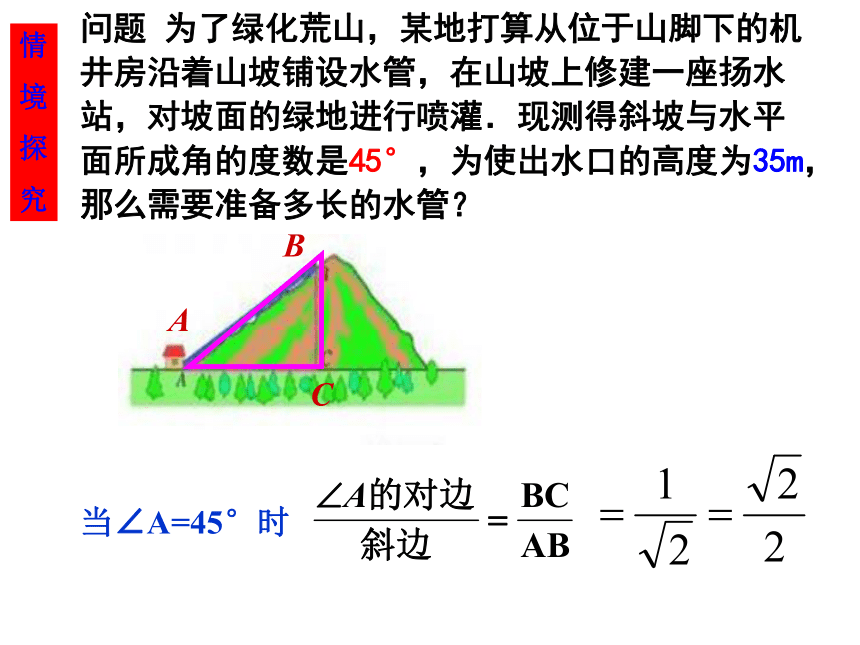
究当∠A=30°时如果使出水口的高度为50m,那么需要准备多长的水管?∴AB=2BC=70m答:需要准备70m长的水管。问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是45°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
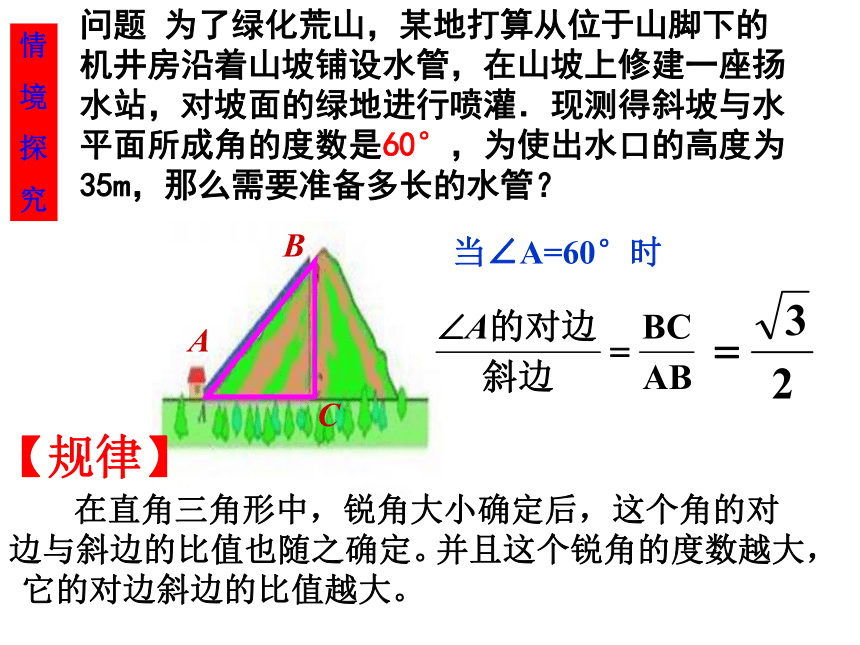
究当∠A=45°时问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是60°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
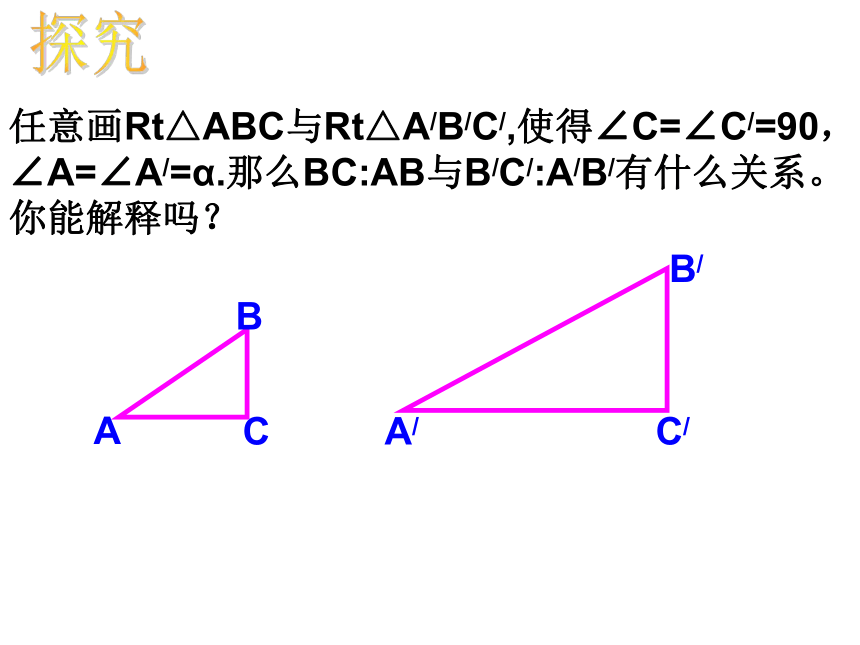
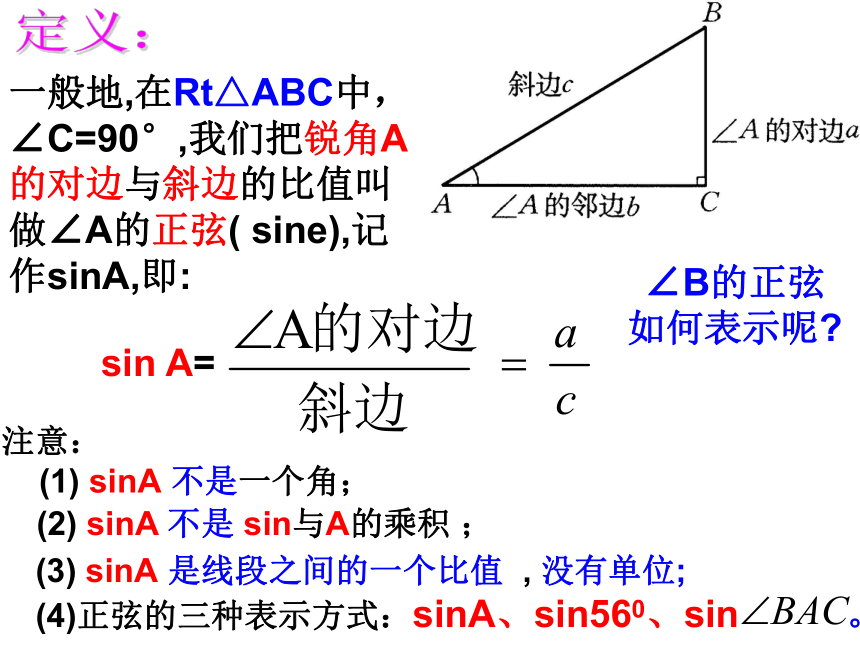
究当∠A=60°时【规律】 在直角三角形中,锐角大小确定后,这个角的对边与斜边的比值也随之确定。 并且这个锐角的度数越大,它的对边斜边的比值越大。探究任意画Rt△ABC与Rt△A/B/C/,使得∠C=∠C/=90,∠A=∠A/=α.那么BC:AB与B/C/:A/B/有什么关系。你能解释吗?一般地,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦( sine),记作sinA,即:sin A= ∠B的正弦如何表示呢?注意:
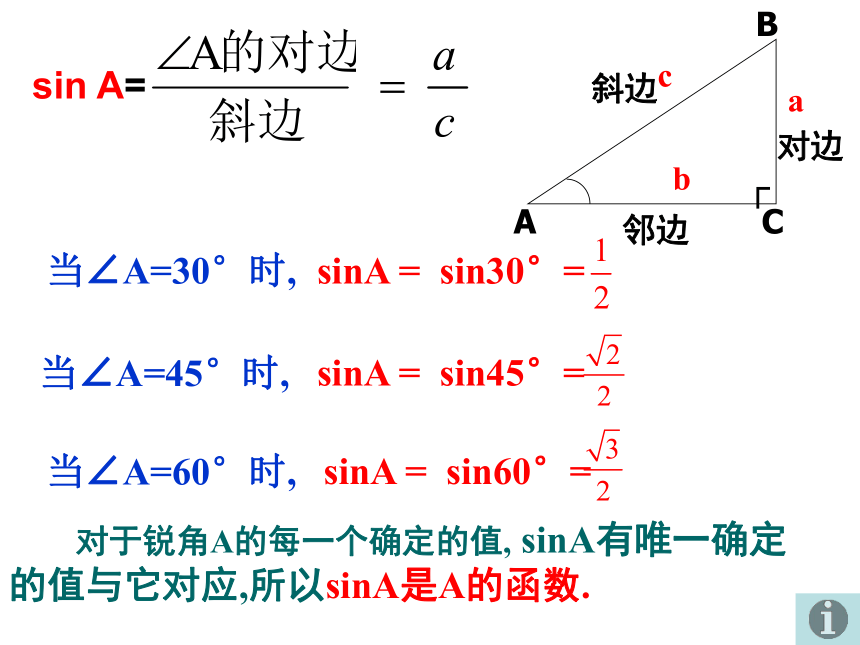
(1) sinA 不是一个角;定义:(2) sinA 不是 sin与A的乘积 ; (3) sinA 是线段之间的一个比值 , 没有单位;(4)正弦的三种表示方式:sinA、sin560、sin 。 对于锐角A的每一个确定的值, sinA有唯一确定的值与它对应,所以sinA是A的函数.当∠A=30°时,sinA = sin30°=当∠A=45°时,sinA = sin45°=sin A= 当∠A=60°时,sinA = sin60°=练一练1.判断对错:1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)sinB=0.8 ( )
√√××sinA是线段之间的一个比值(注意比的顺序),无单位;2)如图,sinA= ( ) ×2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定C练一练练一练4.如图,在Rt △ABC中,∠C=90°,AB=13,BC=5
求sinA和sinB的值.解:在Rt △ABC中,5、根据下图,求sinA和sinB的值.C3 自主练习6、如图,∠C=900,AB= ,BC= ,
求∠A的度数。BCA7、如图,P为角a的一边OA上的任一点,过P作PQ ⊥OB于点Q,则a的正弦函数值与( )
A、角a的大小无关 B、点P的位置无关
C、角a的度数无关 D、OP的长度有关OPABQa 求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。 如图, ∠C=90°,CD⊥AB,
sinB可以由哪两条线段之比?想一想若AC=5,CD=3,求sinB的值。解: ∵∠B =∠ACD ∴sinB = sin∠ACD在Rt△ACD中,AD=sin ∠ACD=∴sinB==4 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足0.77≤ sinα ≤0.97.现有一个长6m的梯子,问使用这个梯子能安全攀上一个5m 高的平房吗?实际应用ACB1.在△ABC中,∠C=900,sinA+sinB= ,
AC+BC=28,求AB的长.挑战自我3.已知△ABC中,∠ACB=900,CD⊥AB于D,若AB=5,BC=4,求sinα的值.2、如图,在△ABC中, AB=AC=5,sinB= ,求△ABC 的面积。D3.△ABC中,AB=8,BC=6,S△ABC=12,试求sinB的值.D回味无穷 1.锐角三角函数中正弦函数定义: 2.sinA是∠A的函数. sin300 = ;sin45°= ;sin60°=注意:(1) sinA 不是一个角,它有三种表达方式;(2) sinA不是 sin与A的乘积; (3) sinA 是线段之间的一个比值, 没有单位。 3.角的正弦值的计算:(1)直接在直角三角形中利用定义计算。(2)通过构造直角三角形进行计算。(3)转化为求与之相等的角的正弦值。今天作业:1 作业本(2) P17 2 课时作业本 P5、在平面直角坐标系中,有一条直线m:y=5/12x,m与x轴的正半轴的夹角为α,求sinα的值。拓展提高6.已知在Rt△ABC中,∠C=900,D是BC中点,DE⊥AB,垂足为E,sin∠BDE= ,
AE=7,求DE的长.
只有量的变化,才会有质的进步。[思考] 操场上有一旗杆,老师让小明去测量它的高度。 小明站在离旗杆底部10m远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高1m,然后他很快就算出旗杆的高度了。 你知道小明是怎样算出的吗?3401米10米28.1 锐角三角函数(1)——正 弦问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
究当∠A=30°时如果使出水口的高度为50m,那么需要准备多长的水管?∴AB=2BC=70m答:需要准备70m长的水管。问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是45°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
究当∠A=45°时问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是60°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
究当∠A=60°时【规律】 在直角三角形中,锐角大小确定后,这个角的对边与斜边的比值也随之确定。 并且这个锐角的度数越大,它的对边斜边的比值越大。探究任意画Rt△ABC与Rt△A/B/C/,使得∠C=∠C/=90,∠A=∠A/=α.那么BC:AB与B/C/:A/B/有什么关系。你能解释吗?一般地,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦( sine),记作sinA,即:sin A= ∠B的正弦如何表示呢?注意:
(1) sinA 不是一个角;定义:(2) sinA 不是 sin与A的乘积 ; (3) sinA 是线段之间的一个比值 , 没有单位;(4)正弦的三种表示方式:sinA、sin560、sin 。 对于锐角A的每一个确定的值, sinA有唯一确定的值与它对应,所以sinA是A的函数.当∠A=30°时,sinA = sin30°=当∠A=45°时,sinA = sin45°=sin A= 当∠A=60°时,sinA = sin60°=练一练1.判断对错:1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)sinB=0.8 ( )
√√××sinA是线段之间的一个比值(注意比的顺序),无单位;2)如图,sinA= ( ) ×2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定C练一练练一练4.如图,在Rt △ABC中,∠C=90°,AB=13,BC=5
求sinA和sinB的值.解:在Rt △ABC中,5、根据下图,求sinA和sinB的值.C3 自主练习6、如图,∠C=900,AB= ,BC= ,
求∠A的度数。BCA7、如图,P为角a的一边OA上的任一点,过P作PQ ⊥OB于点Q,则a的正弦函数值与( )
A、角a的大小无关 B、点P的位置无关
C、角a的度数无关 D、OP的长度有关OPABQa 求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。 如图, ∠C=90°,CD⊥AB,
sinB可以由哪两条线段之比?想一想若AC=5,CD=3,求sinB的值。解: ∵∠B =∠ACD ∴sinB = sin∠ACD在Rt△ACD中,AD=sin ∠ACD=∴sinB==4 要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足0.77≤ sinα ≤0.97.现有一个长6m的梯子,问使用这个梯子能安全攀上一个5m 高的平房吗?实际应用ACB1.在△ABC中,∠C=900,sinA+sinB= ,
AC+BC=28,求AB的长.挑战自我3.已知△ABC中,∠ACB=900,CD⊥AB于D,若AB=5,BC=4,求sinα的值.2、如图,在△ABC中, AB=AC=5,sinB= ,求△ABC 的面积。D3.△ABC中,AB=8,BC=6,S△ABC=12,试求sinB的值.D回味无穷 1.锐角三角函数中正弦函数定义: 2.sinA是∠A的函数. sin300 = ;sin45°= ;sin60°=注意:(1) sinA 不是一个角,它有三种表达方式;(2) sinA不是 sin与A的乘积; (3) sinA 是线段之间的一个比值, 没有单位。 3.角的正弦值的计算:(1)直接在直角三角形中利用定义计算。(2)通过构造直角三角形进行计算。(3)转化为求与之相等的角的正弦值。今天作业:1 作业本(2) P17 2 课时作业本 P5、在平面直角坐标系中,有一条直线m:y=5/12x,m与x轴的正半轴的夹角为α,求sinα的值。拓展提高6.已知在Rt△ABC中,∠C=900,D是BC中点,DE⊥AB,垂足为E,sin∠BDE= ,
AE=7,求DE的长.
