人教版数学八年级上册第十二章《全等三角形》小结与复习 课件(共18张PPT)
文档属性
| 名称 | 人教版数学八年级上册第十二章《全等三角形》小结与复习 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 656.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 11:33:07 | ||
图片预览

文档简介
(共18张PPT)
《全等三角形》小结与复习
八年级上册第十二章
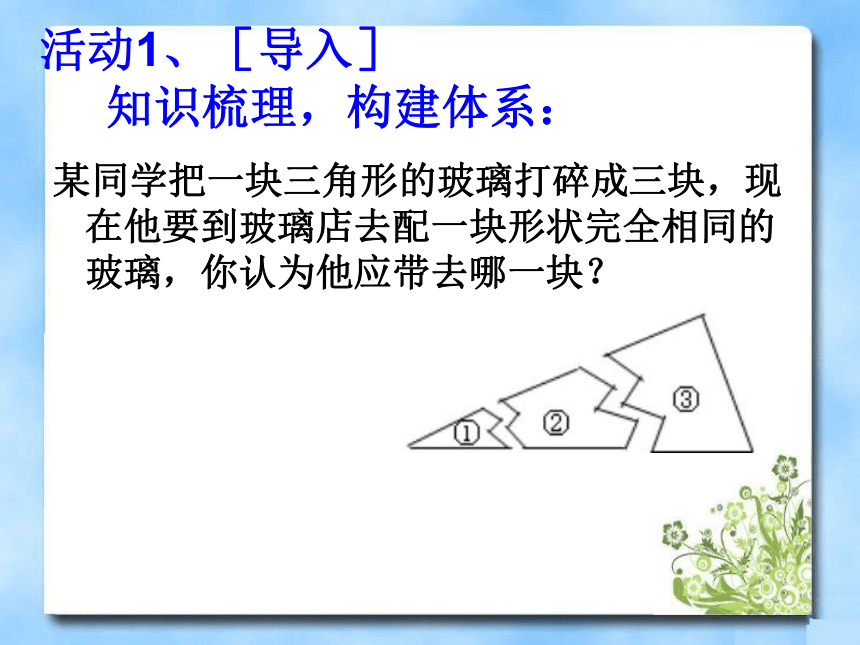
活动1、[导入]
知识梳理,构建体系:
某同学把一块三角形的玻璃打碎成三块,现在他要到玻璃店去配一块形状完全相同的玻璃,你认为他应带去哪一块?
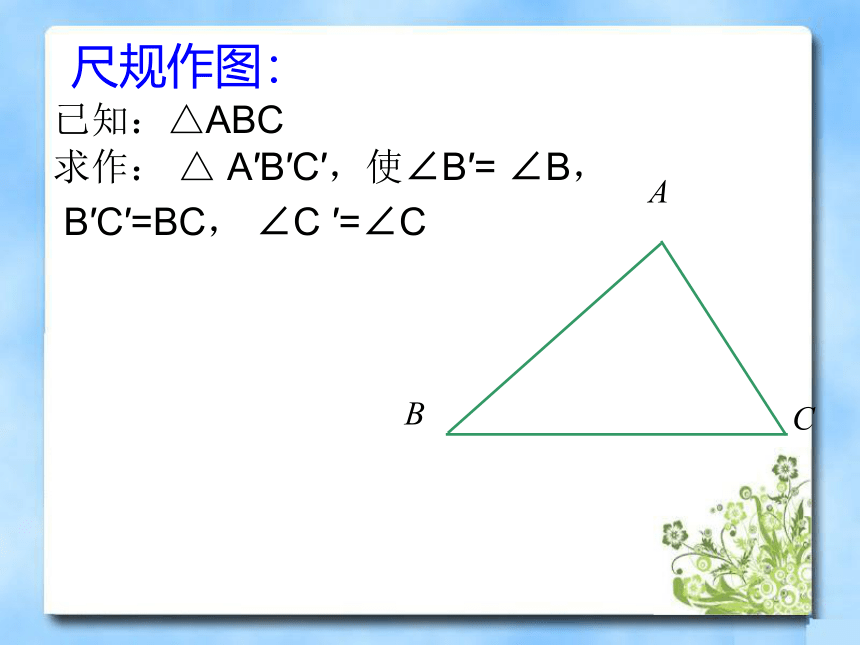
已知:△ABC
A
B
C
求作: △ A′B′C′,使∠B′= ∠B,
B′C′=BC, ∠C ′=∠C
尺规作图:
全等形
全等三角形
边边边,边角边,角边角
角角边,斜边、直角边
角平分线的
性质与判定
应用
对应边相等
对应角相等
尺规作图
能够完全重合
的两个图形
能够完全重合
的两个三角形
全等三角形具有什么性质?
判定两个三角形全等,
有哪些方法?
对角的平分线有了哪
些新的认识?
1、作角等于已知角
2、作已知角的平分线
3、作一个三角形与已
知三角形全等
判定
性质
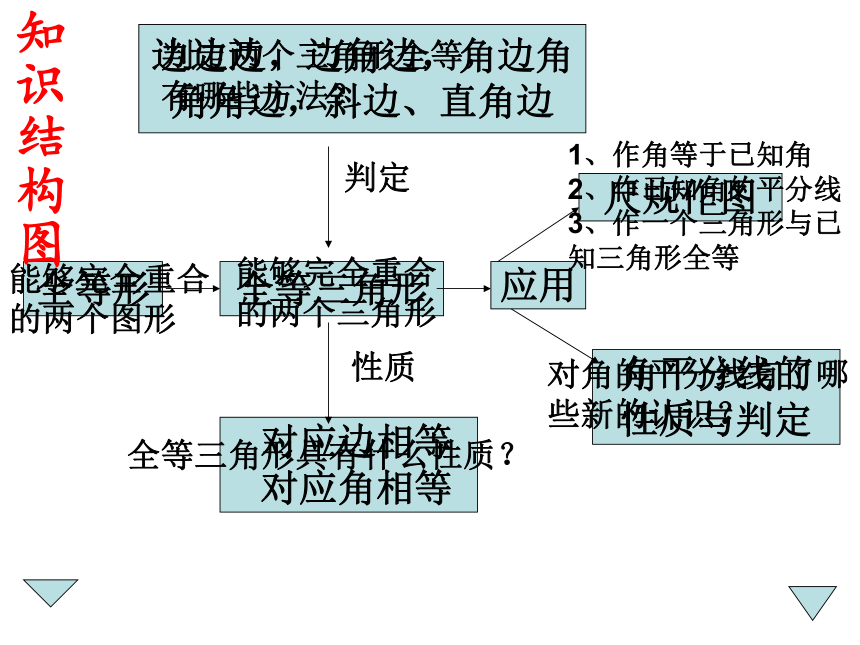
知识结构图
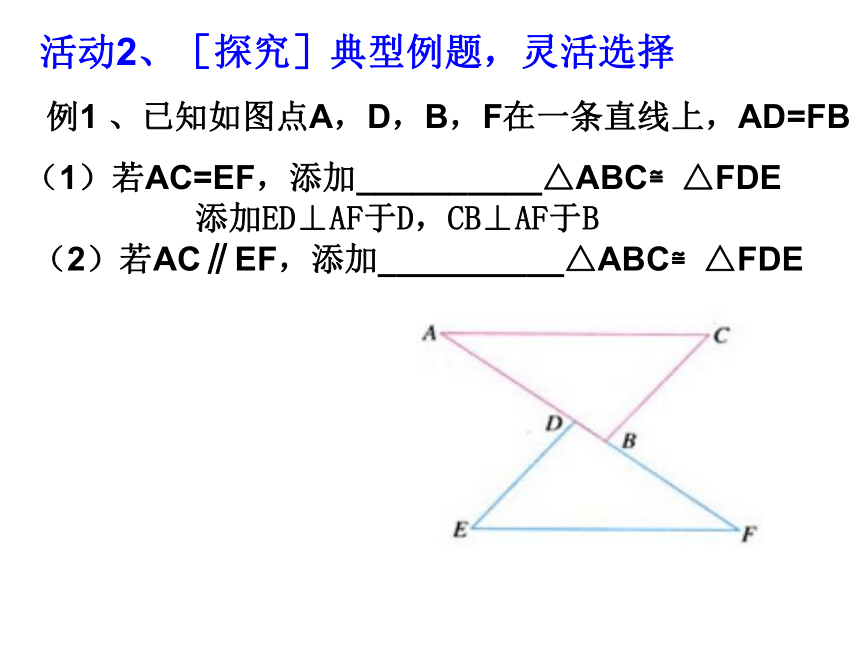
例1 、已知如图点A,D,B,F在一条直线上,AD=FB
活动2、[探究]典型例题,灵活选择
(1)若AC=EF,添加__________△ABC≌△FDE
(2)若AC∥EF,添加__________△ABC≌△FDE
添加ED⊥AF于D,CB⊥AF于B
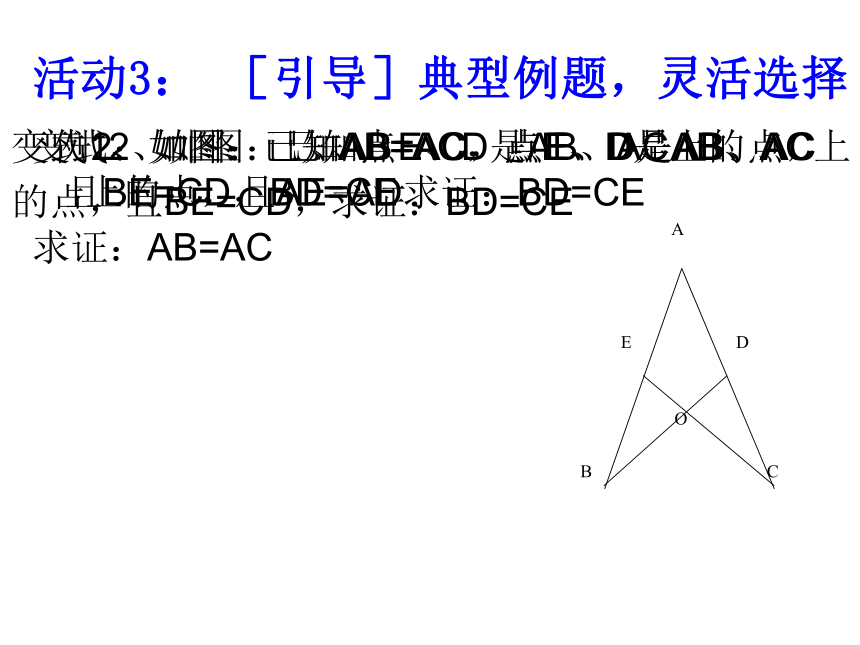
活动3: [引导]典型例题,灵活选择
例2:如图:已知AB=AC,点E、D是AB、AC上的点,且AE=AD求证:BD=CE
A
B
C
D
E
O
变式1、如图:已知AB=AC,点E、D是AB、AC上
的点,且BE=CD,求证:BD=CE
变式2、如图:已知点E、D是AB、AC上的点,且BE=CD,BD=CE
求证:AB=AC
∵BM是△ABC的角平分线, PD⊥AB , PE⊥BC
∴PD=PE.
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
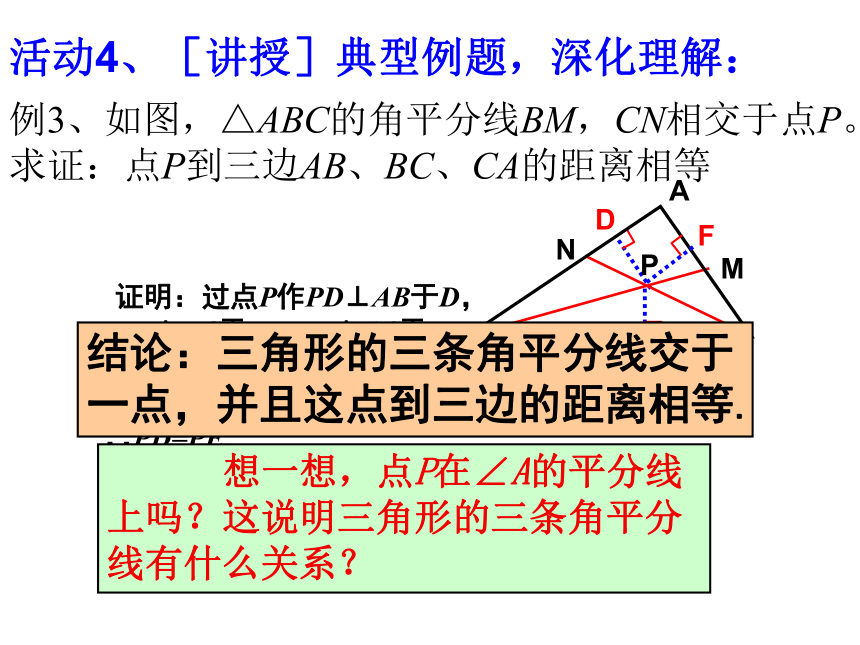
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
例3、如图,△ABC的角平分线BM,CN相交于点P。求证:点P到三边AB、BC、CA的距离相等
D
P
M
N
A
B
C
F
E
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
活动4、[讲授]典型例题,深化理解:
G
H
M
如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠BAC的平分线上.
活动5:变式训练,巩固提高
如图所示,直线 表示三条相互交叉的公
路,现要建一个货物中转站,要求它到三条
公路的距离相等,你能说出可供选择的地址有
几处吗?
P1
P2
P3
P4
l1
l3
S区
l2
如图所示,直线 表示三条相互交叉的公路,现要在s区建一个货物中转站,要求它到三条公
路的距离相等,你能确定中转站的位置吗?
学以致用
活动6、总结归纳,提炼升华
全等三角形的概念、性质、判定方法, 角平分线的性质与判定,尺规作图。
用分析法分析条件与结论的关系。
用综合法书写证明格式。
证明线段或角相等问题往往转化成
证明三角形全等的问题。
思想
方法
知识
B
活动7、目标检测、反馈矫正
1、下列说法错误的是( )
A、有两角和一边分别相等的两个三角形全等
B、有两边和一角分别相等的两个三角形全等
C、有两边和其中一边上的中线分别相等的两个
三角形全等
D、有一边分别相等的两个等边三角形全等
2、如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;
A
B
C
D
AB=AC
∠BDA=∠CDA
∠B=∠C
3、如图所示,要测量河两岸相对的两点A、B的距离,在AB的垂线BF上取两点C、D,使BC=CD,过D作BF的垂线DE,与AC的延长线交于点E,若测得DE的长为25米,则河宽AB长为_______.
25米
4、 如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( ) 作法: ①以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E; ②分别以D,E为圆心,大于1/2DE的长为半径画弧,两弧在∠AOB内交于一点C; ③画射线OC,射线OC就是∠AOB的角平分线. A、ASA B、SAS C、SSS D、AAS
C
5、如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,
④ ∠FAC=∠EAB,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
C
M
O
N
A
B
C
D
P
活动8、拓展延伸:
木工师傅利用手中的角尺采用下列的方法找到角的平分线,你能用所学的知识解释其中的道理吗?
如图:
1、已知∠MON
2、在角的两边上分别截取线段OA=OB,
则OP平分∠MON
3、连接AD、BC交于点P
OC=OD
A
A
C
B
D
E
图1
图2
图3
图4
A
B
D
C
A
B
C
D
B
C
N
M
F
E
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。
角的内部到角的两边的距离相等的点在角的平
分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平 分线上
∴ QD=QE
角的平分线的性质与判定
1.角平分线的性质:
2.角平分线的判定:
《全等三角形》小结与复习
八年级上册第十二章
活动1、[导入]
知识梳理,构建体系:
某同学把一块三角形的玻璃打碎成三块,现在他要到玻璃店去配一块形状完全相同的玻璃,你认为他应带去哪一块?
已知:△ABC
A
B
C
求作: △ A′B′C′,使∠B′= ∠B,
B′C′=BC, ∠C ′=∠C
尺规作图:
全等形
全等三角形
边边边,边角边,角边角
角角边,斜边、直角边
角平分线的
性质与判定
应用
对应边相等
对应角相等
尺规作图
能够完全重合
的两个图形
能够完全重合
的两个三角形
全等三角形具有什么性质?
判定两个三角形全等,
有哪些方法?
对角的平分线有了哪
些新的认识?
1、作角等于已知角
2、作已知角的平分线
3、作一个三角形与已
知三角形全等
判定
性质
知识结构图
例1 、已知如图点A,D,B,F在一条直线上,AD=FB
活动2、[探究]典型例题,灵活选择
(1)若AC=EF,添加__________△ABC≌△FDE
(2)若AC∥EF,添加__________△ABC≌△FDE
添加ED⊥AF于D,CB⊥AF于B
活动3: [引导]典型例题,灵活选择
例2:如图:已知AB=AC,点E、D是AB、AC上的点,且AE=AD求证:BD=CE
A
B
C
D
E
O
变式1、如图:已知AB=AC,点E、D是AB、AC上
的点,且BE=CD,求证:BD=CE
变式2、如图:已知点E、D是AB、AC上的点,且BE=CD,BD=CE
求证:AB=AC
∵BM是△ABC的角平分线, PD⊥AB , PE⊥BC
∴PD=PE.
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等.
证明:过点P作PD⊥AB于D,
PE⊥BC于E,PF⊥AC于F,
例3、如图,△ABC的角平分线BM,CN相交于点P。求证:点P到三边AB、BC、CA的距离相等
D
P
M
N
A
B
C
F
E
想一想,点P在∠A的平分线上吗?这说明三角形的三条角平分线有什么关系?
结论:三角形的三条角平分线交于一点,并且这点到三边的距离相等.
活动4、[讲授]典型例题,深化理解:
G
H
M
如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠BAC的平分线上.
活动5:变式训练,巩固提高
如图所示,直线 表示三条相互交叉的公
路,现要建一个货物中转站,要求它到三条
公路的距离相等,你能说出可供选择的地址有
几处吗?
P1
P2
P3
P4
l1
l3
S区
l2
如图所示,直线 表示三条相互交叉的公路,现要在s区建一个货物中转站,要求它到三条公
路的距离相等,你能确定中转站的位置吗?
学以致用
活动6、总结归纳,提炼升华
全等三角形的概念、性质、判定方法, 角平分线的性质与判定,尺规作图。
用分析法分析条件与结论的关系。
用综合法书写证明格式。
证明线段或角相等问题往往转化成
证明三角形全等的问题。
思想
方法
知识
B
活动7、目标检测、反馈矫正
1、下列说法错误的是( )
A、有两角和一边分别相等的两个三角形全等
B、有两边和一角分别相等的两个三角形全等
C、有两边和其中一边上的中线分别相等的两个
三角形全等
D、有一边分别相等的两个等边三角形全等
2、如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;
A
B
C
D
AB=AC
∠BDA=∠CDA
∠B=∠C
3、如图所示,要测量河两岸相对的两点A、B的距离,在AB的垂线BF上取两点C、D,使BC=CD,过D作BF的垂线DE,与AC的延长线交于点E,若测得DE的长为25米,则河宽AB长为_______.
25米
4、 如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( ) 作法: ①以O为圆心,适当长为半径画弧,分别交OA,OB于点D,E; ②分别以D,E为圆心,大于1/2DE的长为半径画弧,两弧在∠AOB内交于一点C; ③画射线OC,射线OC就是∠AOB的角平分线. A、ASA B、SAS C、SSS D、AAS
C
5、如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,
④ ∠FAC=∠EAB,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
C
M
O
N
A
B
C
D
P
活动8、拓展延伸:
木工师傅利用手中的角尺采用下列的方法找到角的平分线,你能用所学的知识解释其中的道理吗?
如图:
1、已知∠MON
2、在角的两边上分别截取线段OA=OB,
则OP平分∠MON
3、连接AD、BC交于点P
OC=OD
A
A
C
B
D
E
图1
图2
图3
图4
A
B
D
C
A
B
C
D
B
C
N
M
F
E
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。
角的内部到角的两边的距离相等的点在角的平
分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平 分线上
∴ QD=QE
角的平分线的性质与判定
1.角平分线的性质:
2.角平分线的判定:
