人教版数学八年级上册全等三角形性质与判定的综合应用 课件(共16张PPT)
文档属性
| 名称 | 人教版数学八年级上册全等三角形性质与判定的综合应用 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 581.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 11:29:19 | ||
图片预览



文档简介
(共16张PPT)
全等三角形性质与判定的综合应用
一、知识回顾
1、全等三角形的概念及其性质
全等三角形的概念:
能够完全重合的两个三角形叫做全等三角形 ,重合的点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
全等三角形性质:
(1) 对应边相等 (2)对应角相等
(3)周长相等 (4)面积相等
注意:“全等”的记法“≌”,全等变换:平移、旋转、翻转
2、全等三角形的判定方法:
一般三角形 全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:
HL
包括直角三角形
不包括其它形状的三角形
解题中常用的4种方法
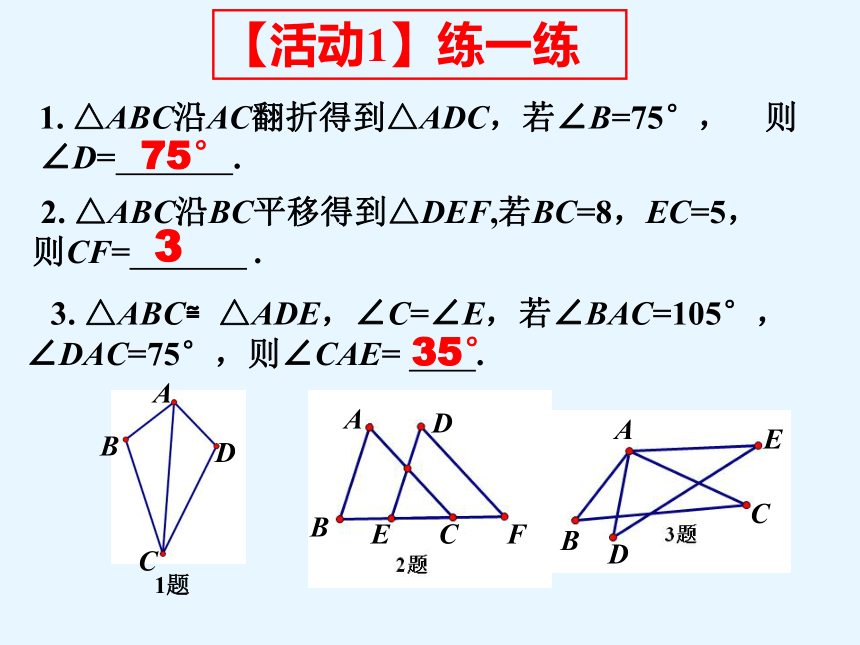
【活动1】练一练
1. △ABC沿AC翻折得到△ADC,若∠B=75°, 则∠D= .
2. △ABC沿BC平移得到△DEF,若BC=8,EC=5,
则CF= .
3. △ABC≌△ADE,∠C=∠E,若∠BAC=105°,
∠DAC=75°,则∠CAE= .
75°
3
35°
B
A
C
D
1题
A
B
C
E
F
D
A
E
B
D
C
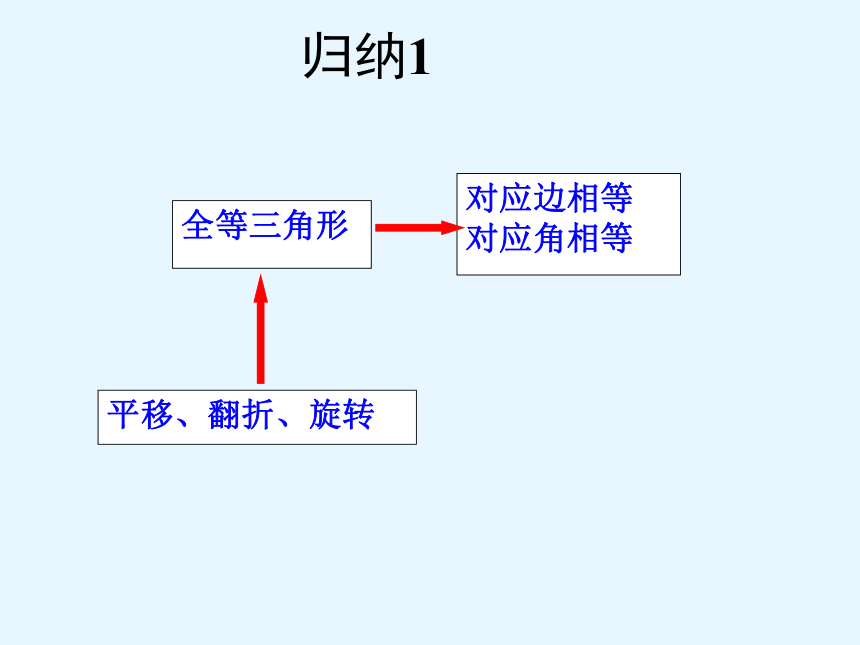
归纳1
全等三角形
对应边相等
对应角相等
平移、翻折、旋转
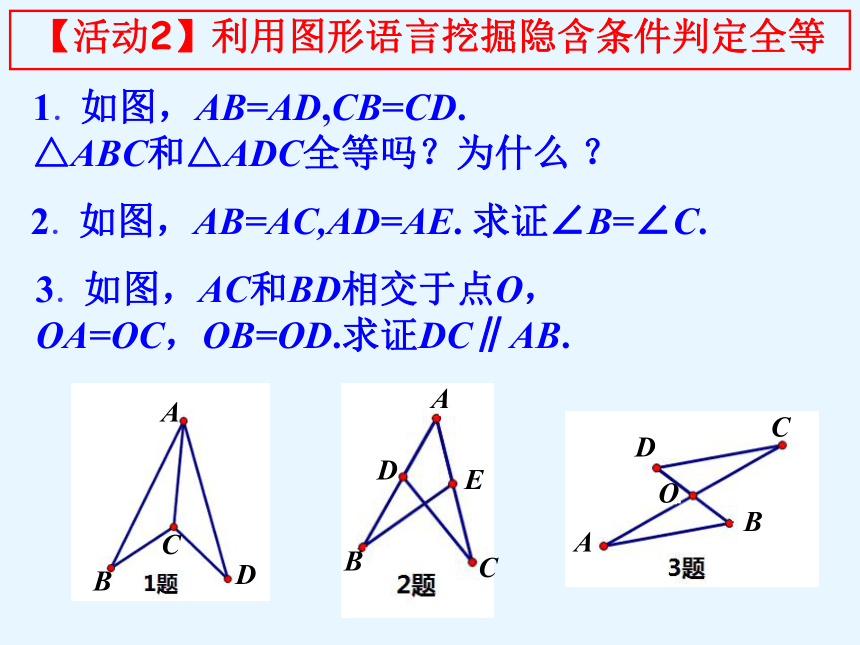
【活动2】利用图形语言挖掘隐含条件判定全等
2.如图,AB=AC,AD=AE. 求证∠B=∠C.
3.如图,AC和BD相交于点O,
OA=OC,OB=OD.求证DC∥AB.
1.如图,AB=AD,CB=CD.
△ABC和△ADC全等吗?为什么 ?
A
B
D
C
A
E
B
D
C
A
O
B
D
C
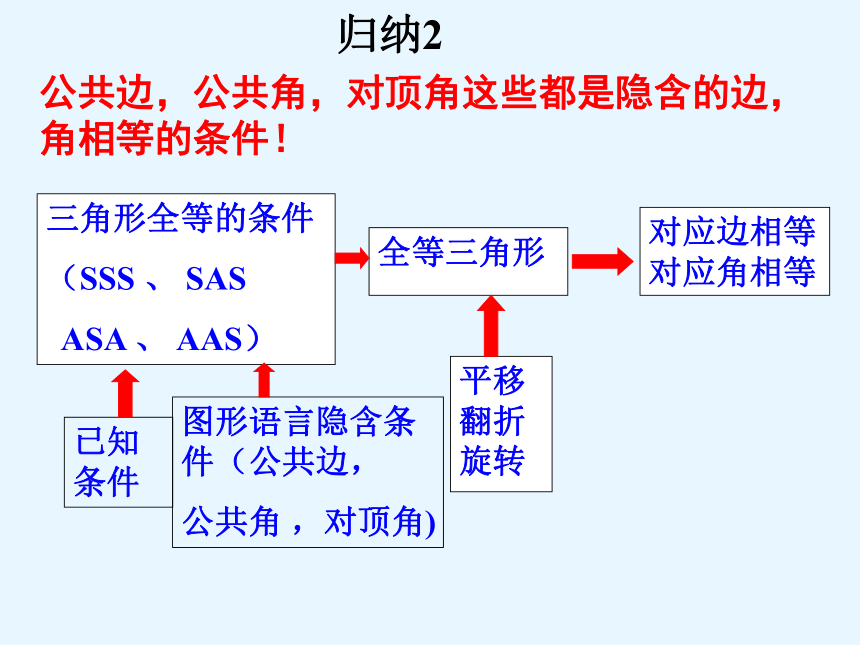
归纳2
公共边,公共角,对顶角这些都是隐含的边,角相等的条件!
全等三角形
对应边相等
对应角相等
平移
翻折
旋转
三角形全等的条件
(SSS 、 SAS
ASA 、 AAS)
已知条件
图形语言隐含条件(公共边,
公共角 ,对顶角)
A
B
D
C
1.如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 .
AB=AC
∠BDA=∠CDA
∠B=∠C
友情提示:添加条件的题目,首先要找到已具备的条件,这些条件有些是题目已知条件 ,有些是图中隐含条件.
【活动3】添条件判全等
A
B
D
C
2. 如图,已知AC=BD, 要使△ABC≌△DCB,根
据“SSS”需要添加条件 ;根据“SAS”需要添
加条件 .
已知条件
隐含条件
增添条件
AC=BD
BC=CB
AB=CD
∠ABC=∠DCB
AB=CD
∠ABC=∠DCB
根据SSS
根据SAS
3.如图,BD与AC相交于点O,∠A=∠C,要使△ABO≌△CDO,
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 .
已知条件
隐含条件
增添条件
∠ A= ∠ C
∠ AOB= ∠ COD
OA=OC
OD=OB或DC=AB
OA=OC
OD=OB
或DC=AB
A
O
B
D
C
归纳3
全等三角形
三角形全等的条件
(SSS 、 SAS 、ASA 、AAS)
已知条件
图形语言隐含条件(公共边,公共角, 对顶角)
增添条件
A
E
B
D
C
证明: ∵ ∠CAE=∠BAD,
∴∠CAE+∠BAE=∠BAD+∠BAE,
即∠BAC=∠DAE.
又∵∠B=∠D,
AC=AE,
△ABC≌ △ADE,
∴AD=AB(全等三角形的对应边相等).
根据“AAS”,就可以得到
如图,∠CAE=∠BAD,∠B=∠D,AC=AE.求证:AD=AB.
【活动4 】转化间接条件,判断全等
归纳4
全等三角形
三角形全等的条件
(SSS 、 SAS 、ASA 、AAS)
已知条件
图形语言隐含条件(公共边公共角 对顶角)
间接条件
对应边相等
对应角相等
利用线段和差证出对应边相等;利用角的和差或平行线的性质证出对应角相等.
转化
【活动5】归纳小结,总结方法
1.本节课主要解决了哪些问题 你对解决全等的习题有了哪些认识?
2.本节课的学习中哪些环节给你留下的印象最深刻 你还有什么疑问
【活动7】布置作业
教材第44页第10、11题,第45页第12题.
谢 谢
全等三角形性质与判定的综合应用
一、知识回顾
1、全等三角形的概念及其性质
全等三角形的概念:
能够完全重合的两个三角形叫做全等三角形 ,重合的点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
全等三角形性质:
(1) 对应边相等 (2)对应角相等
(3)周长相等 (4)面积相等
注意:“全等”的记法“≌”,全等变换:平移、旋转、翻转
2、全等三角形的判定方法:
一般三角形 全等的条件:
1.定义(重合)法;
2.SSS;
3.SAS;
4.ASA;
5.AAS.
直角三角形 全等特有的条件:
HL
包括直角三角形
不包括其它形状的三角形
解题中常用的4种方法
【活动1】练一练
1. △ABC沿AC翻折得到△ADC,若∠B=75°, 则∠D= .
2. △ABC沿BC平移得到△DEF,若BC=8,EC=5,
则CF= .
3. △ABC≌△ADE,∠C=∠E,若∠BAC=105°,
∠DAC=75°,则∠CAE= .
75°
3
35°
B
A
C
D
1题
A
B
C
E
F
D
A
E
B
D
C
归纳1
全等三角形
对应边相等
对应角相等
平移、翻折、旋转
【活动2】利用图形语言挖掘隐含条件判定全等
2.如图,AB=AC,AD=AE. 求证∠B=∠C.
3.如图,AC和BD相交于点O,
OA=OC,OB=OD.求证DC∥AB.
1.如图,AB=AD,CB=CD.
△ABC和△ADC全等吗?为什么 ?
A
B
D
C
A
E
B
D
C
A
O
B
D
C
归纳2
公共边,公共角,对顶角这些都是隐含的边,角相等的条件!
全等三角形
对应边相等
对应角相等
平移
翻折
旋转
三角形全等的条件
(SSS 、 SAS
ASA 、 AAS)
已知条件
图形语言隐含条件(公共边,
公共角 ,对顶角)
A
B
D
C
1.如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 .
AB=AC
∠BDA=∠CDA
∠B=∠C
友情提示:添加条件的题目,首先要找到已具备的条件,这些条件有些是题目已知条件 ,有些是图中隐含条件.
【活动3】添条件判全等
A
B
D
C
2. 如图,已知AC=BD, 要使△ABC≌△DCB,根
据“SSS”需要添加条件 ;根据“SAS”需要添
加条件 .
已知条件
隐含条件
增添条件
AC=BD
BC=CB
AB=CD
∠ABC=∠DCB
AB=CD
∠ABC=∠DCB
根据SSS
根据SAS
3.如图,BD与AC相交于点O,∠A=∠C,要使△ABO≌△CDO,
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 .
已知条件
隐含条件
增添条件
∠ A= ∠ C
∠ AOB= ∠ COD
OA=OC
OD=OB或DC=AB
OA=OC
OD=OB
或DC=AB
A
O
B
D
C
归纳3
全等三角形
三角形全等的条件
(SSS 、 SAS 、ASA 、AAS)
已知条件
图形语言隐含条件(公共边,公共角, 对顶角)
增添条件
A
E
B
D
C
证明: ∵ ∠CAE=∠BAD,
∴∠CAE+∠BAE=∠BAD+∠BAE,
即∠BAC=∠DAE.
又∵∠B=∠D,
AC=AE,
△ABC≌ △ADE,
∴AD=AB(全等三角形的对应边相等).
根据“AAS”,就可以得到
如图,∠CAE=∠BAD,∠B=∠D,AC=AE.求证:AD=AB.
【活动4 】转化间接条件,判断全等
归纳4
全等三角形
三角形全等的条件
(SSS 、 SAS 、ASA 、AAS)
已知条件
图形语言隐含条件(公共边公共角 对顶角)
间接条件
对应边相等
对应角相等
利用线段和差证出对应边相等;利用角的和差或平行线的性质证出对应角相等.
转化
【活动5】归纳小结,总结方法
1.本节课主要解决了哪些问题 你对解决全等的习题有了哪些认识?
2.本节课的学习中哪些环节给你留下的印象最深刻 你还有什么疑问
【活动7】布置作业
教材第44页第10、11题,第45页第12题.
谢 谢
