人教版数学八年级上册15.3.可化为一元一次方程的分式方程 课件(共19张PPT)
文档属性
| 名称 | 人教版数学八年级上册15.3.可化为一元一次方程的分式方程 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
学以至用
数学来源于生活
生活离不开数学
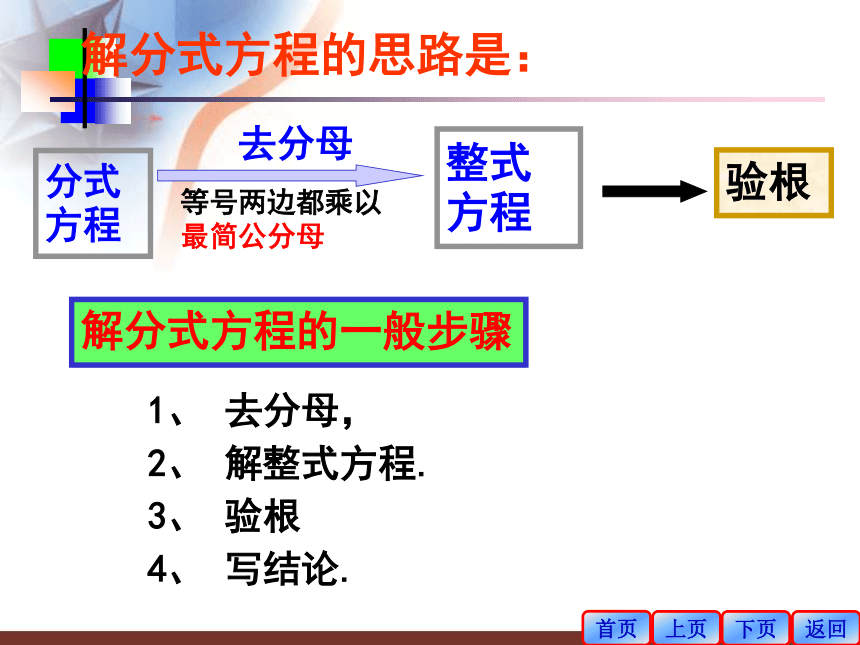
解分式方程的一般步骤
1、 去分母,
2、 解整式方程.
3、 验根
4、 写结论.
解分式方程的思路是:
分式方程
整式方程
去分母
验根
等号两边都乘以
最简公分母
解方程 :
(1)
(2)
(3)
(4)
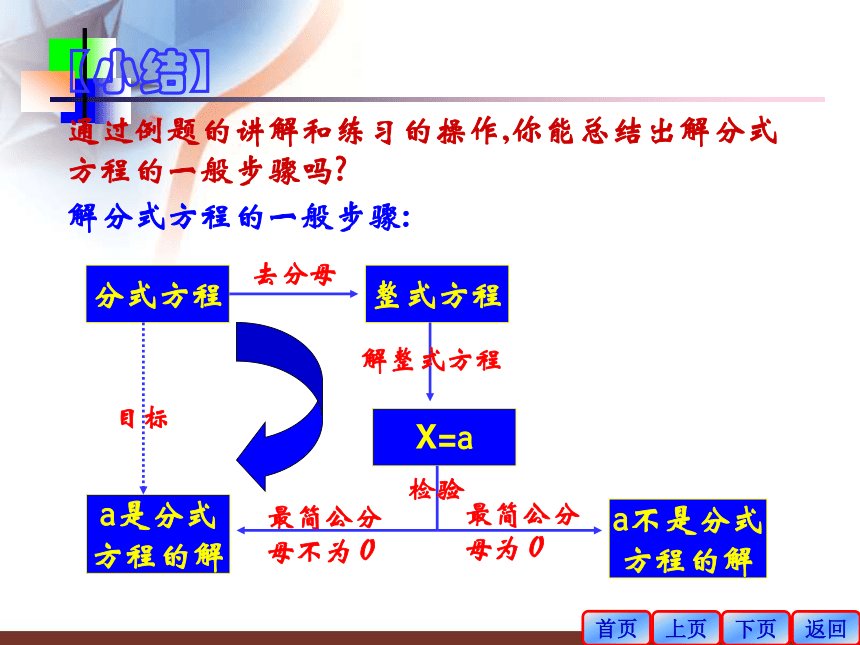
通过例题的讲解和练习的操作,你能总结出解分式方程的一般步骤吗
【小结】
解分式方程的一般步骤:
分式方程
整式方程
a是分式
方程的解
X=a
a不是分式
方程的解
去分母
解整式方程
检验
目标
最简公分
母不为0
最简公分
母为0
1.若方程中的分母是多项式,须先分解因式.再确定最简公分母.
2.若方程中的含有整数项,去分母时不要漏乘.
例3.当k为何值时,方程 的解为负数
解:方程两边都乘以x-2,得
解这个整式方程,得
k+3(x-2)=x-1
变式.当k为何值时,方程 的解为正数
所以当k=1时,方程 产生增根。
例4.当a为何值时,方程 有增根
解:去分母,方程两边同乘以
解这个整式方程,得
因为方程有增根,所以
所以
所以当
时,原方程产生增根.
k为何值时,方程 无解?
思考:“方程有增根”和“方程无解”一样吗?
变式1:
k为何值时,方程 有解?
变式2:
例5.已知
例题讲解与练习
变式 解方程:
解:
方程两边分别通分
经检验 是原方程的根
∴原方程的根是 .
所以
解得
例6.解关于 的分式方程
解:去分母,方程两边同乘以
移项,得
所以
所以
经检验
是原方程的根.
因为
1.判断:
做一做
做一做
2.解下列分式方程:
做一做
3.解下列分式方程:
做一做
4.解关于 的分式方程:
5.已知分式方程 无解,求 的值.
做一做
6. 为何值时,分式方程
有根
解分式方程的注意点:
(1)去分母时,先确定最简公分母;若分母是多项式,要进行因式分解;
(2)去分母时,不要漏乘不含分母的项;
(3)最后不要忘记验根。
课堂小结
学以至用
数学来源于生活
生活离不开数学
解分式方程的一般步骤
1、 去分母,
2、 解整式方程.
3、 验根
4、 写结论.
解分式方程的思路是:
分式方程
整式方程
去分母
验根
等号两边都乘以
最简公分母
解方程 :
(1)
(2)
(3)
(4)
通过例题的讲解和练习的操作,你能总结出解分式方程的一般步骤吗
【小结】
解分式方程的一般步骤:
分式方程
整式方程
a是分式
方程的解
X=a
a不是分式
方程的解
去分母
解整式方程
检验
目标
最简公分
母不为0
最简公分
母为0
1.若方程中的分母是多项式,须先分解因式.再确定最简公分母.
2.若方程中的含有整数项,去分母时不要漏乘.
例3.当k为何值时,方程 的解为负数
解:方程两边都乘以x-2,得
解这个整式方程,得
k+3(x-2)=x-1
变式.当k为何值时,方程 的解为正数
所以当k=1时,方程 产生增根。
例4.当a为何值时,方程 有增根
解:去分母,方程两边同乘以
解这个整式方程,得
因为方程有增根,所以
所以
所以当
时,原方程产生增根.
k为何值时,方程 无解?
思考:“方程有增根”和“方程无解”一样吗?
变式1:
k为何值时,方程 有解?
变式2:
例5.已知
例题讲解与练习
变式 解方程:
解:
方程两边分别通分
经检验 是原方程的根
∴原方程的根是 .
所以
解得
例6.解关于 的分式方程
解:去分母,方程两边同乘以
移项,得
所以
所以
经检验
是原方程的根.
因为
1.判断:
做一做
做一做
2.解下列分式方程:
做一做
3.解下列分式方程:
做一做
4.解关于 的分式方程:
5.已知分式方程 无解,求 的值.
做一做
6. 为何值时,分式方程
有根
解分式方程的注意点:
(1)去分母时,先确定最简公分母;若分母是多项式,要进行因式分解;
(2)去分母时,不要漏乘不含分母的项;
(3)最后不要忘记验根。
课堂小结
