人教版数学九年级上册第二十三章 旋转23.2 中心对称上册23.2.1中心对称 课件(共21张PPT)
文档属性
| 名称 | 人教版数学九年级上册第二十三章 旋转23.2 中心对称上册23.2.1中心对称 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
观察:下列图形,绕中心点旋转多少度能与自身重合?它们的旋转角度有什么相同点?
(1) 这些图形有什么共同的特征?
(2)这些图形都可以绕某个点旋转哪个角度后与原来的图形重合
在平面内,一个图形绕某个点旋转180o,能与自身重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
特征:(1)中心对称图形绕着它的中心点旋转180°后与自身重合;(2)中心对称图形也是一种特殊的旋转对称图形。
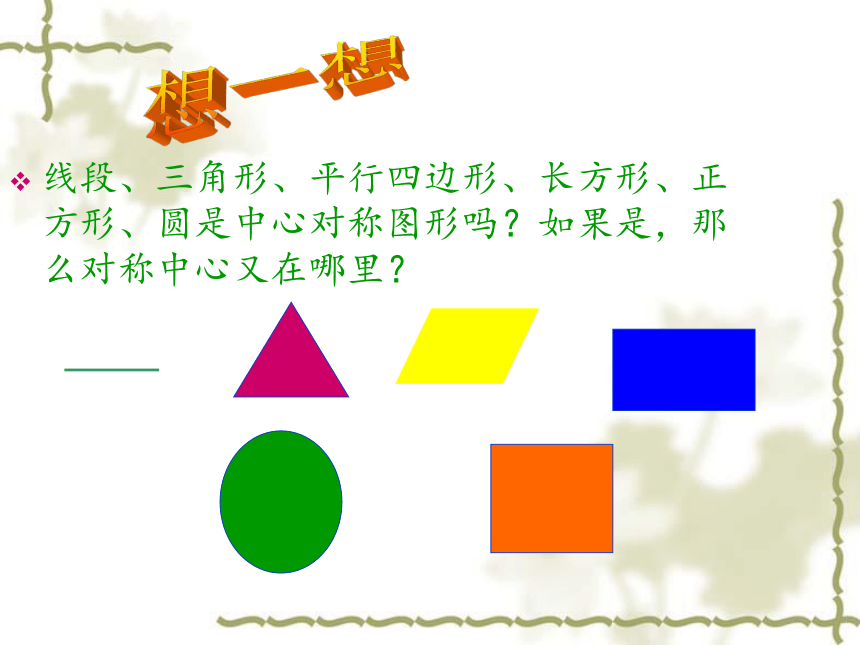
线段、三角形、平行四边形、长方形、正方形、圆是中心对称图形吗?如果是,那么对称中心又在哪里?
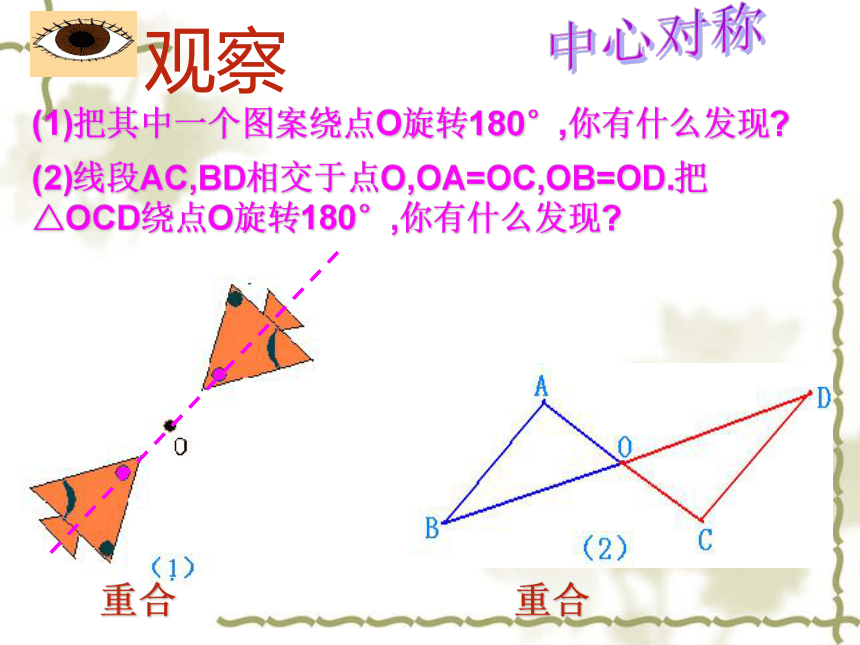
(1)把其中一个图案绕点O旋转180°,你有什么发现
重合
重合
观察
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现
A
C
B
A
C
B
A
C
B
A
D
E
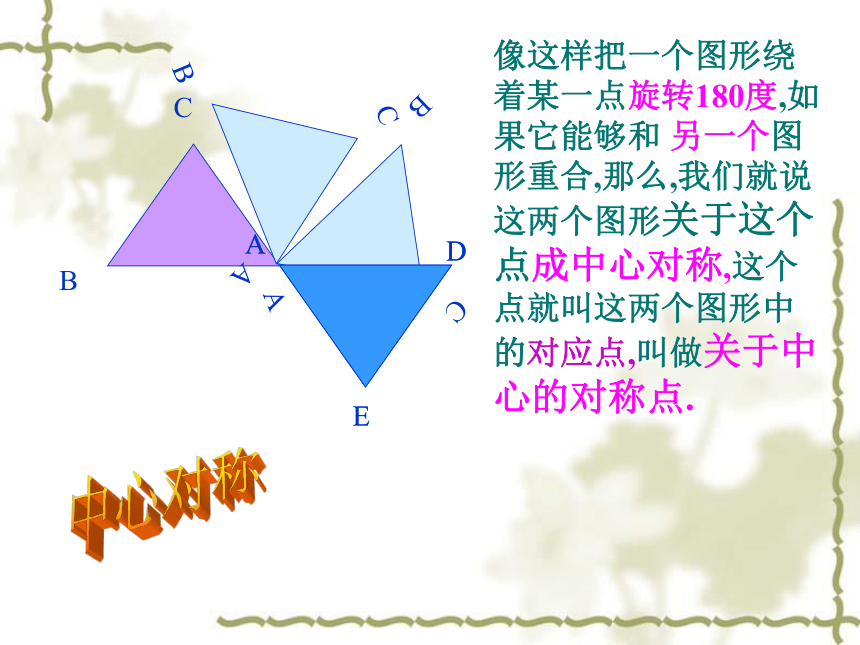
像这样把一个图形绕着某一点旋转180度,如果它能够和 另一个图形重合,那么,我们就说这两个图形关于这个点成中心对称,这个点就叫这两个图形中的对应点,叫做关于中心的对称点.
A
D
E
请你探究
中心对称图形与中心对称的区别:
中心对称图形 中心对称
相同点
不同点
VS
请你动手:将一个三角板放在纸上,画出△ABC,再将三角板绕一个顶点旋转180o,画出△A’B’C’,移开三角板,画出的△ABC与△A’B’C’关于点O对称。分别连接对称点AA’ 、BB’、CC’,点O在线段AA’上吗?如果在,在什么位置? △ABC与 △A’B’C’有什么关系?
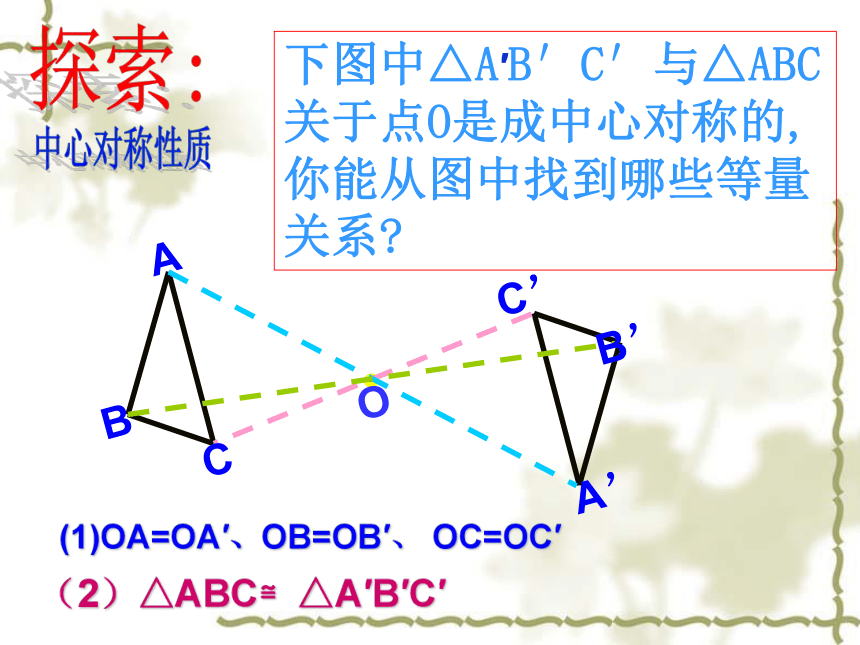
下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系
A’
B’
C’
A
B
C
O
(1)OA=OA′、OB=OB′、 OC=OC′
(2)△ABC≌△A′B′C′
归纳:
在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
试一试:如果△ABC和△EDF关于点O成中心对称,写出相等的线段和相等的角。
D
E
F
A
A′
B′
B
O
2、线段的中心对称线段的作法
A
O
A′
1、点的中心对称点的作法
灵活运用,体会内涵
以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
线段A′B′就是所求的线段
点A′即为所求的点
应用拓展 :已知四边形ABCD和点O(下图),画四边形A’B’C’D’,使它与已知四边形关于点O对称.
.
o
A
B
C
D
A’
B’
C’
D’
画法:1. 连结AO并延长到A’,使
OA’=OA,得到点A的对称点A’.
2. 同样画B、C、D的对称点
B’、C’、D’.
3. 顺次连结A’、B’、C’、D’
各点.
四边形A’B’C’D’就是所求的四边形.
巩固练习:如图23.2-5,选择点O为对称中心,画出与△ABC关于点O对称的△A’B’C’.
能力提高 : 已知四边形ABCD,画四边形A’B’C’D’,使它与已知四边形关于点A对称。
解:
A
B
C
D
1、判断下列图形是否是中心对称图形
达标检测一
2、画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。
达标检测二
D
A
B
C
E
F
G
M
D
A
B
C
O
.
N
1、回顾本节课的活动过程 。
2、本节课学到了哪些知识?
——应用
(1)中心对称图形与中心对称的定义
(2)中心对称的性质
(3)我们所学的多边形中有哪些是中心对称图形
(4)中心对称的应用
观察
——分析
——探索
——概括
小结: 今天你学到了什么
自己设计一个中心对称图形,并画出它关于某点成中心对称的图形。
课后作业
板书设计
15.3 中心对称
1、中心对称图形
2、中心对称
(1)定义
(2)性质
(3)应用
教学评价
课堂教学是一个动态过程,学生的思维又常常受到课堂气氛的影响,为了达到最佳的教学效果,我将“教学反应”型评价和“教学反馈”型评价相结合,一方面根据课堂实施状况和学生反馈的信息而作出一种即时性评价;另一方面根据课堂练习的反馈,了解学生掌握知识的程度,灵活安排教学细节,从而达到教学的预期效果。
观察:下列图形,绕中心点旋转多少度能与自身重合?它们的旋转角度有什么相同点?
(1) 这些图形有什么共同的特征?
(2)这些图形都可以绕某个点旋转哪个角度后与原来的图形重合
在平面内,一个图形绕某个点旋转180o,能与自身重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
特征:(1)中心对称图形绕着它的中心点旋转180°后与自身重合;(2)中心对称图形也是一种特殊的旋转对称图形。
线段、三角形、平行四边形、长方形、正方形、圆是中心对称图形吗?如果是,那么对称中心又在哪里?
(1)把其中一个图案绕点O旋转180°,你有什么发现
重合
重合
观察
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现
A
C
B
A
C
B
A
C
B
A
D
E
像这样把一个图形绕着某一点旋转180度,如果它能够和 另一个图形重合,那么,我们就说这两个图形关于这个点成中心对称,这个点就叫这两个图形中的对应点,叫做关于中心的对称点.
A
D
E
请你探究
中心对称图形与中心对称的区别:
中心对称图形 中心对称
相同点
不同点
VS
请你动手:将一个三角板放在纸上,画出△ABC,再将三角板绕一个顶点旋转180o,画出△A’B’C’,移开三角板,画出的△ABC与△A’B’C’关于点O对称。分别连接对称点AA’ 、BB’、CC’,点O在线段AA’上吗?如果在,在什么位置? △ABC与 △A’B’C’有什么关系?
下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系
A’
B’
C’
A
B
C
O
(1)OA=OA′、OB=OB′、 OC=OC′
(2)△ABC≌△A′B′C′
归纳:
在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
试一试:如果△ABC和△EDF关于点O成中心对称,写出相等的线段和相等的角。
D
E
F
A
A′
B′
B
O
2、线段的中心对称线段的作法
A
O
A′
1、点的中心对称点的作法
灵活运用,体会内涵
以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
线段A′B′就是所求的线段
点A′即为所求的点
应用拓展 :已知四边形ABCD和点O(下图),画四边形A’B’C’D’,使它与已知四边形关于点O对称.
.
o
A
B
C
D
A’
B’
C’
D’
画法:1. 连结AO并延长到A’,使
OA’=OA,得到点A的对称点A’.
2. 同样画B、C、D的对称点
B’、C’、D’.
3. 顺次连结A’、B’、C’、D’
各点.
四边形A’B’C’D’就是所求的四边形.
巩固练习:如图23.2-5,选择点O为对称中心,画出与△ABC关于点O对称的△A’B’C’.
能力提高 : 已知四边形ABCD,画四边形A’B’C’D’,使它与已知四边形关于点A对称。
解:
A
B
C
D
1、判断下列图形是否是中心对称图形
达标检测一
2、画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。
达标检测二
D
A
B
C
E
F
G
M
D
A
B
C
O
.
N
1、回顾本节课的活动过程 。
2、本节课学到了哪些知识?
——应用
(1)中心对称图形与中心对称的定义
(2)中心对称的性质
(3)我们所学的多边形中有哪些是中心对称图形
(4)中心对称的应用
观察
——分析
——探索
——概括
小结: 今天你学到了什么
自己设计一个中心对称图形,并画出它关于某点成中心对称的图形。
课后作业
板书设计
15.3 中心对称
1、中心对称图形
2、中心对称
(1)定义
(2)性质
(3)应用
教学评价
课堂教学是一个动态过程,学生的思维又常常受到课堂气氛的影响,为了达到最佳的教学效果,我将“教学反应”型评价和“教学反馈”型评价相结合,一方面根据课堂实施状况和学生反馈的信息而作出一种即时性评价;另一方面根据课堂练习的反馈,了解学生掌握知识的程度,灵活安排教学细节,从而达到教学的预期效果。
同课章节目录
