人教版数学八年级上册11.3.2 多边形及其内角和 课件(共21张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.3.2 多边形及其内角和 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 451.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 12:59:26 | ||
图片预览





文档简介
(共21张PPT)
11.3 多边形的内角和
课标要求:
探索并掌握多边形内角和与外角和公式。
学习目标:
1.了解多边形内角和公式以及运用公式进行有关计算
2.理解运用多边形外角和公式
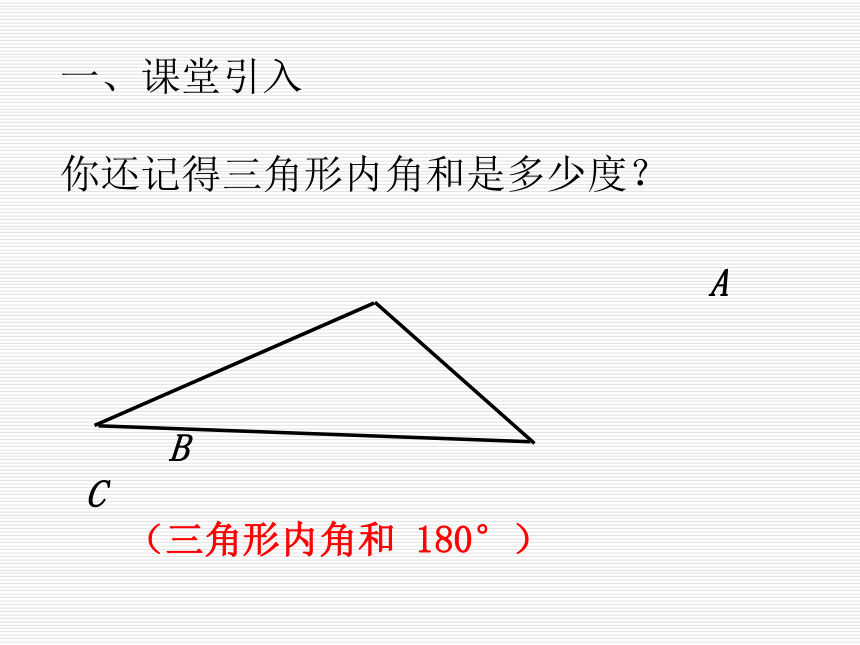
一、课堂引入
你还记得三角形内角和是多少度?
A
B C
(三角形内角和 180°)
你知道长方形和正方形内角和是多少吗?
A
D
B
C
A
D
B
C
(都是360°)
A
B
C
D
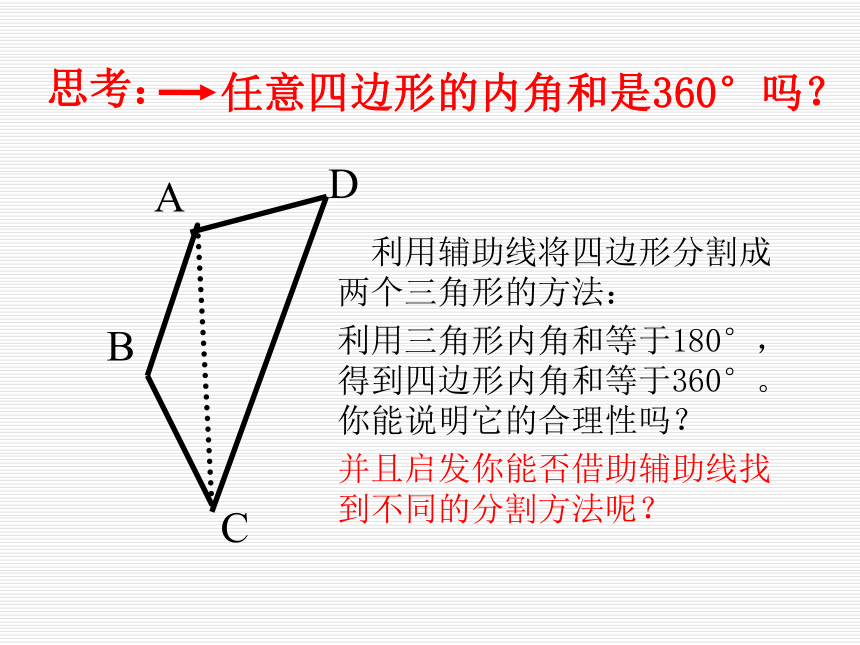
利用辅助线将四边形分割成两个三角形的方法:
利用三角形内角和等于180°,得到四边形内角和等于360°。你能说明它的合理性吗?
并且启发你能否借助辅助线找到不同的分割方法呢?
任意四边形的内角和是360°吗?
思考:
P
A
B
C
D
图 1
如图1,在四边形内任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,
四边形内角和等于
180°×4 - 360°= 360°
二、学生自主学习
P
A
B
D
C
图 2
如图2,在四边形的一边上任取一点P,连接PB、PC,将四边形变成有一个公共顶点的三个三角形,四边形内角和等于
180° ×3-180°= 360°
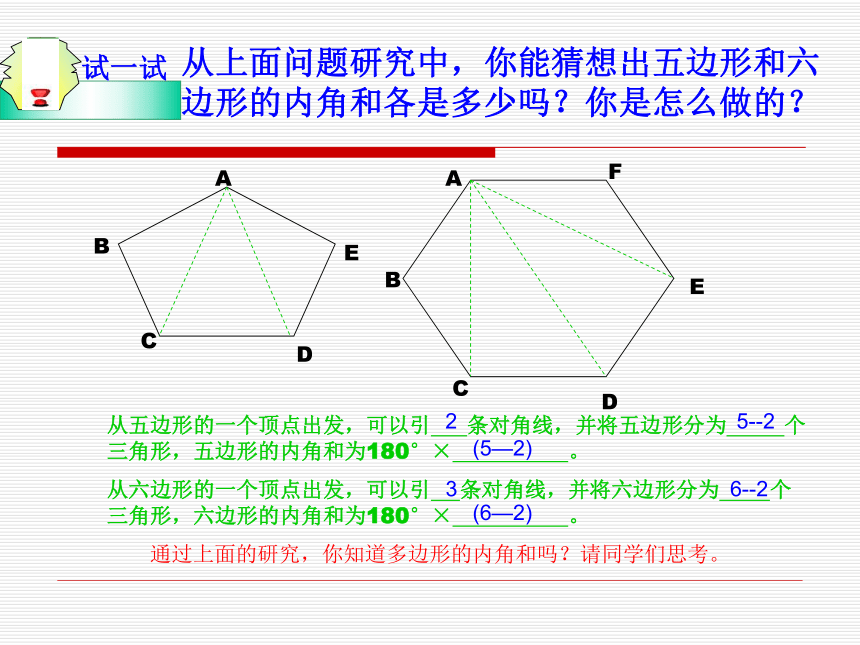
从上面问题研究中,你能猜想出五边形和六边形的内角和各是多少吗?你是怎么做的?
A
B
C
D
E
A
B
C
D
E
F
从五边形的一个顶点出发,可以引 条对角线,并将五边形分为 个三角形,五边形的内角和为180°× 。
从六边形的一个顶点出发,可以引 条对角线,并将六边形分为 个三角形,六边形的内角和为180°× 。
通过上面的研究,你知道多边形的内角和吗?请同学们思考。
2
5--2
(5—2)
3
6--2
(6—2)
试一试
多边形的内角和
(1) 三角形个数与多边形边数有何关系?
三角形个数比多边形的边数 少 2。
(2)多边形的内角和与所有三角形的内角和有何关系?
多边形的内角和与所有三角形的内角和 相等
(3)由此你能得到多边形的内角和吗?
从n边形的一个顶点出发,可以引 条对角线,并将n
边形分为 个三角形, n边形的内角和等于 。
(4)你还有其它的方法可以说明多边形的内角和为 吗?
n--3
n--2
180°×(n—2)
180°×(n—2)
提问
返回
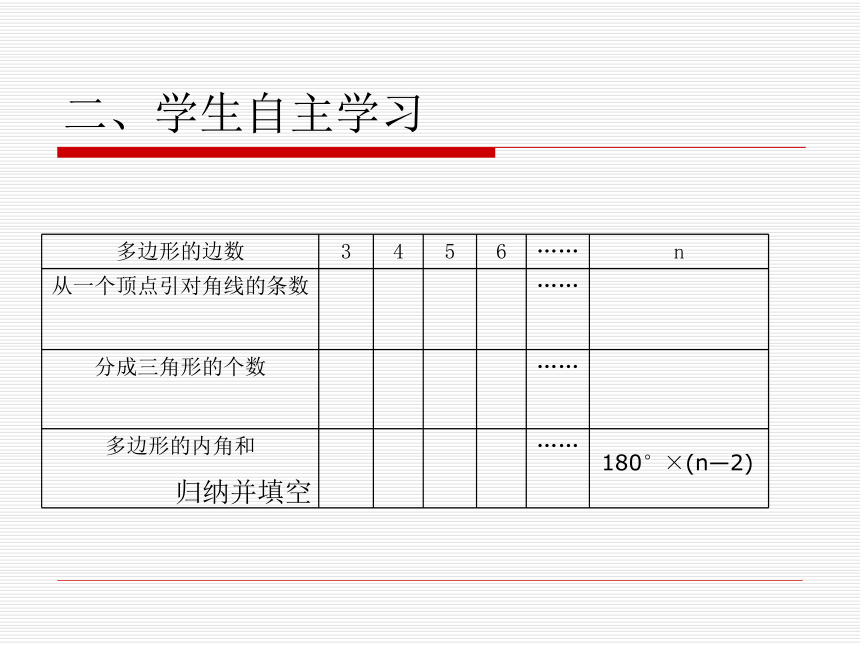
二、学生自主学习
归纳并填空
多边形的边数 3 4 5 6 …… n
从一个顶点引对角线的条数 ……
分成三角形的个数 ……
多边形的内角和 ……
180°×(n—2)
探究
我们也可以利用下列不同的方法分割多边形,得到n边形的内角和公式
p
p
解:如图所示,四边形ABCD中,
∠A+∠C=180。
因为
∠A+∠B+ ∠C+ ∠D=(4-2)×180。 =360。
所以
∠B+ ∠D =360。-( ∠A+∠C )
=360。- 180。
=180。
这就是说,如果四边形的一组对角互补,那么另一组
对角也互补。
A
D
C
B
例2:如图,在六边形的每个顶点处各取一个外角,
这些外角的和叫做六边形的外角和.六边形的外角
和等于多少?
A
B
C
D
E
F
1
2
3
4
5
6
三、例题讲解
∠1 +∠2 +∠3 +∠4 +∠5+∠6
=180°×6 - 180°×4 =360°.
探索n 边形的外角和
问题 你能仿照上面的方法求n 边形(n 是不小
于3 的任意整数)的外角和吗?
因为n 边形的每个内角与它相邻的外角是邻补角,
它们的和是180°,所以n 边形内角和加外角和等于
n · 180°,所以, n 边形的外角和为:
n · 180°-(n -2)· 180°= 360°.
任意多边形的外角和等于360°.
探索n 边形的外角和
我们也可以这样理解多边形外角和等于360°.
如图,从多边形的一
个顶点A 出发,沿多边形
的各边走过各顶点,再回
到点A,然后转向出发的
方向.
A
探索n 边形的外角和
在行程中转过的各个
角的和,就是多边形的外
角和.由于走了一周,所
转过的各个角的和等于一
个周角,所以多边形外角
和等于360°.
A
三、例题讲解
例3、已知一个n边形的内角和与外角和之比
为7:2,求这个多边形的边数n.
四、当堂练习
(A组)一、判断题.
1.当多边形边数增加时,它的内角和也随着增加.( √ )
2.当多边形边数增加时.它的外角和也随着增加.( × )
3.三角形的外角和与一多边形的外角和相等.( √ )
4.从n边形一个顶点出发,可以引出(n一2)条对角线,
得到(n一2)个三角形. ( × )
5.四边形的四个内角至少有一个角不小于直角.( √ )
四、当堂练习
二、填空题.
6.一个多边形的每个内角都等于135°,则这个多边形
为 边形.
7.一个多边形的每一个外角都等于30°,则这个多边形
为 边形.
8.内角和等于外角和的多边形是 边形.
9.内角和为1440°的多边形是 .
10.四边形中∠A、∠B、∠C、∠D的外角之比为1:2:
3:4,那么∠A:∠B:∠C:∠D= .
8
12
4
10边形
4:3:2:1
四、当堂练习
三、选择题
11.多边形的每个外角与它相邻内角的关系是 ( )
A.互为余角 B.互为邻补角
C.两个角相等 D.外角大于内角
(B组) 12.一个多边形的内角和为720°,那么这个
多边形的对角线条数为( )
A.6条 B.7条 C.8条 D.9条
13. n边形的n个内角中锐角最多有( )个.
A.1个 B.2个 C.3个 D.4个
B
D
C
四、当堂练习
14、选作题:(C组)
一个多边形除一个内角外,其余的各内角之和为2570°.求这个内角的度数。
课堂小结
1、我们学会了许多解决数学问题的思想方法,如将多边形问题转化为三角形问题,以及类比方法,化未知为已知的思想方法等。
2、通过探索多边形的内角和公式,我们尝试了从不同的角度寻求解决问题的方法,并且能有效地解决问题。
3、我们还学会了运用多边形内角和公式进行相关计算。
11.3 多边形的内角和
课标要求:
探索并掌握多边形内角和与外角和公式。
学习目标:
1.了解多边形内角和公式以及运用公式进行有关计算
2.理解运用多边形外角和公式
一、课堂引入
你还记得三角形内角和是多少度?
A
B C
(三角形内角和 180°)
你知道长方形和正方形内角和是多少吗?
A
D
B
C
A
D
B
C
(都是360°)
A
B
C
D
利用辅助线将四边形分割成两个三角形的方法:
利用三角形内角和等于180°,得到四边形内角和等于360°。你能说明它的合理性吗?
并且启发你能否借助辅助线找到不同的分割方法呢?
任意四边形的内角和是360°吗?
思考:
P
A
B
C
D
图 1
如图1,在四边形内任取一点P,连接PA、PB、PC、PD将四边形变成有一个公共顶点的四个三角形,
四边形内角和等于
180°×4 - 360°= 360°
二、学生自主学习
P
A
B
D
C
图 2
如图2,在四边形的一边上任取一点P,连接PB、PC,将四边形变成有一个公共顶点的三个三角形,四边形内角和等于
180° ×3-180°= 360°
从上面问题研究中,你能猜想出五边形和六边形的内角和各是多少吗?你是怎么做的?
A
B
C
D
E
A
B
C
D
E
F
从五边形的一个顶点出发,可以引 条对角线,并将五边形分为 个三角形,五边形的内角和为180°× 。
从六边形的一个顶点出发,可以引 条对角线,并将六边形分为 个三角形,六边形的内角和为180°× 。
通过上面的研究,你知道多边形的内角和吗?请同学们思考。
2
5--2
(5—2)
3
6--2
(6—2)
试一试
多边形的内角和
(1) 三角形个数与多边形边数有何关系?
三角形个数比多边形的边数 少 2。
(2)多边形的内角和与所有三角形的内角和有何关系?
多边形的内角和与所有三角形的内角和 相等
(3)由此你能得到多边形的内角和吗?
从n边形的一个顶点出发,可以引 条对角线,并将n
边形分为 个三角形, n边形的内角和等于 。
(4)你还有其它的方法可以说明多边形的内角和为 吗?
n--3
n--2
180°×(n—2)
180°×(n—2)
提问
返回
二、学生自主学习
归纳并填空
多边形的边数 3 4 5 6 …… n
从一个顶点引对角线的条数 ……
分成三角形的个数 ……
多边形的内角和 ……
180°×(n—2)
探究
我们也可以利用下列不同的方法分割多边形,得到n边形的内角和公式
p
p
解:如图所示,四边形ABCD中,
∠A+∠C=180。
因为
∠A+∠B+ ∠C+ ∠D=(4-2)×180。 =360。
所以
∠B+ ∠D =360。-( ∠A+∠C )
=360。- 180。
=180。
这就是说,如果四边形的一组对角互补,那么另一组
对角也互补。
A
D
C
B
例2:如图,在六边形的每个顶点处各取一个外角,
这些外角的和叫做六边形的外角和.六边形的外角
和等于多少?
A
B
C
D
E
F
1
2
3
4
5
6
三、例题讲解
∠1 +∠2 +∠3 +∠4 +∠5+∠6
=180°×6 - 180°×4 =360°.
探索n 边形的外角和
问题 你能仿照上面的方法求n 边形(n 是不小
于3 的任意整数)的外角和吗?
因为n 边形的每个内角与它相邻的外角是邻补角,
它们的和是180°,所以n 边形内角和加外角和等于
n · 180°,所以, n 边形的外角和为:
n · 180°-(n -2)· 180°= 360°.
任意多边形的外角和等于360°.
探索n 边形的外角和
我们也可以这样理解多边形外角和等于360°.
如图,从多边形的一
个顶点A 出发,沿多边形
的各边走过各顶点,再回
到点A,然后转向出发的
方向.
A
探索n 边形的外角和
在行程中转过的各个
角的和,就是多边形的外
角和.由于走了一周,所
转过的各个角的和等于一
个周角,所以多边形外角
和等于360°.
A
三、例题讲解
例3、已知一个n边形的内角和与外角和之比
为7:2,求这个多边形的边数n.
四、当堂练习
(A组)一、判断题.
1.当多边形边数增加时,它的内角和也随着增加.( √ )
2.当多边形边数增加时.它的外角和也随着增加.( × )
3.三角形的外角和与一多边形的外角和相等.( √ )
4.从n边形一个顶点出发,可以引出(n一2)条对角线,
得到(n一2)个三角形. ( × )
5.四边形的四个内角至少有一个角不小于直角.( √ )
四、当堂练习
二、填空题.
6.一个多边形的每个内角都等于135°,则这个多边形
为 边形.
7.一个多边形的每一个外角都等于30°,则这个多边形
为 边形.
8.内角和等于外角和的多边形是 边形.
9.内角和为1440°的多边形是 .
10.四边形中∠A、∠B、∠C、∠D的外角之比为1:2:
3:4,那么∠A:∠B:∠C:∠D= .
8
12
4
10边形
4:3:2:1
四、当堂练习
三、选择题
11.多边形的每个外角与它相邻内角的关系是 ( )
A.互为余角 B.互为邻补角
C.两个角相等 D.外角大于内角
(B组) 12.一个多边形的内角和为720°,那么这个
多边形的对角线条数为( )
A.6条 B.7条 C.8条 D.9条
13. n边形的n个内角中锐角最多有( )个.
A.1个 B.2个 C.3个 D.4个
B
D
C
四、当堂练习
14、选作题:(C组)
一个多边形除一个内角外,其余的各内角之和为2570°.求这个内角的度数。
课堂小结
1、我们学会了许多解决数学问题的思想方法,如将多边形问题转化为三角形问题,以及类比方法,化未知为已知的思想方法等。
2、通过探索多边形的内角和公式,我们尝试了从不同的角度寻求解决问题的方法,并且能有效地解决问题。
3、我们还学会了运用多边形内角和公式进行相关计算。
