人教版数学八年级上册11.3.2 多边形的内角和 课件(共16张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.3.2 多边形的内角和 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 538.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
新人教版 八年级(上) 数学 第11章
§11.3.2 多边形的内角和
(第一课时)
学习目标:
重点与难点:
1.知识目标:
了解多边形内角和公式以及运用公式进行有关计算。
2.能力目标:
(1)通过测量、类比、推理等数学活动,探索多边形内角和公式,感受数学思考过程中的条理性,发展推理能力和语言表达能力。
(2)通过把多边形转化为三角形体会转化思想在几何中的运用,同时让学生体会从特殊到一般的认识问题的方法。
重点
探索多边形内角和公式。
难点
探索多边形内角和时,如何把多边形转化为三角形
3.三角形的内角和是_____度.
2.在多边形中连接______________________的线段叫做多边形的对角线。
1.在平面内,___________________________叫做多边形。
由一些线段首尾顺次相接组成的图形
多边形不相邻的两个顶点
180
4.正方形的内角和是 度,长方形的内角和是 度。
360
360
知识回顾
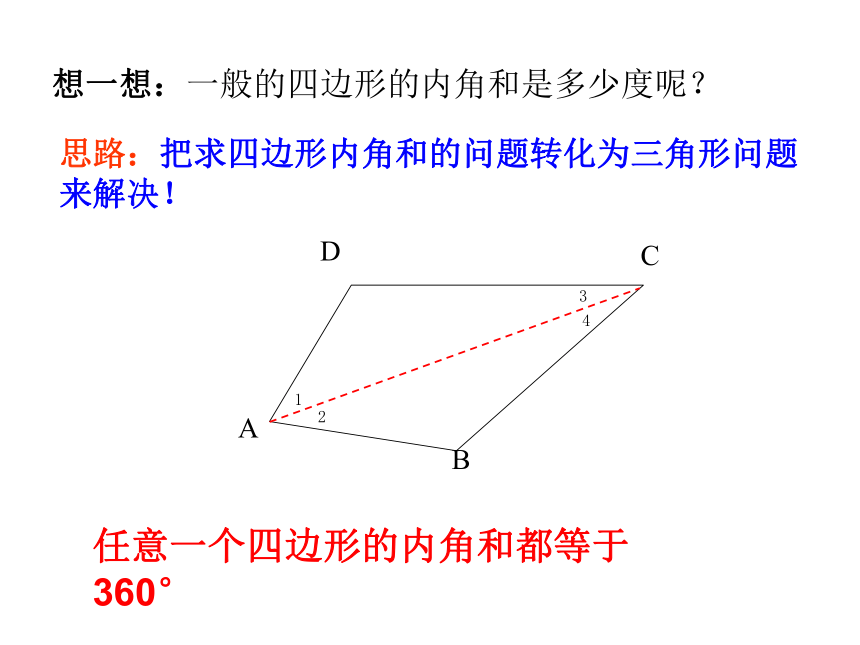
A
B
C
D
任意一个四边形的内角和都等于360°
思路:把求四边形内角和的问题转化为三角形问题来解决!
想一想:一般的四边形的内角和是多少度呢?
1
3
2
4
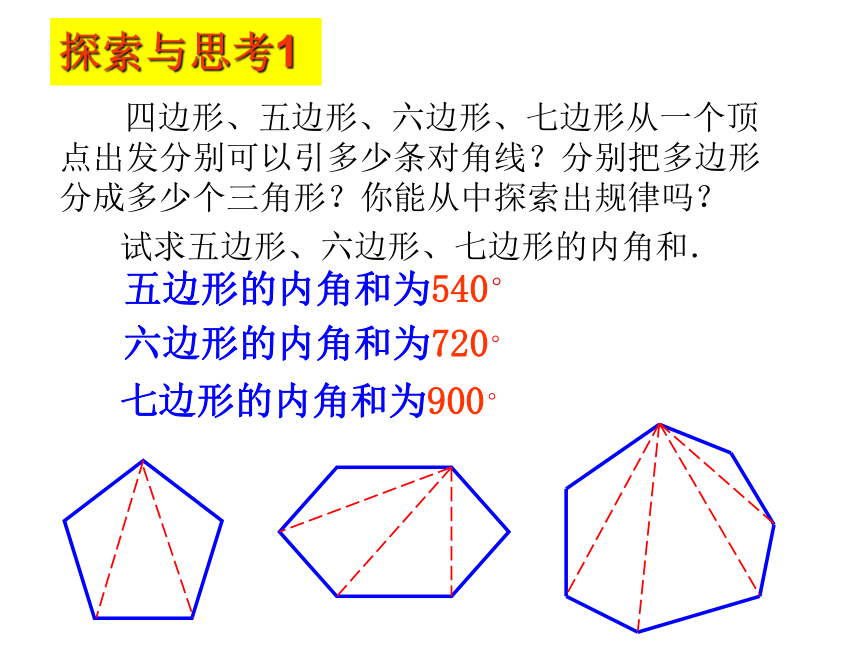
五边形的内角和为540°
七边形的内角和为900°
六边形的内角和为720°
四边形、五边形、六边形、七边形从一个顶点出发分别可以引多少条对角线?分别把多边形分成多少个三角形?你能从中探索出规律吗?
试求五边形、六边形、七边形的内角和.
探索与思考1
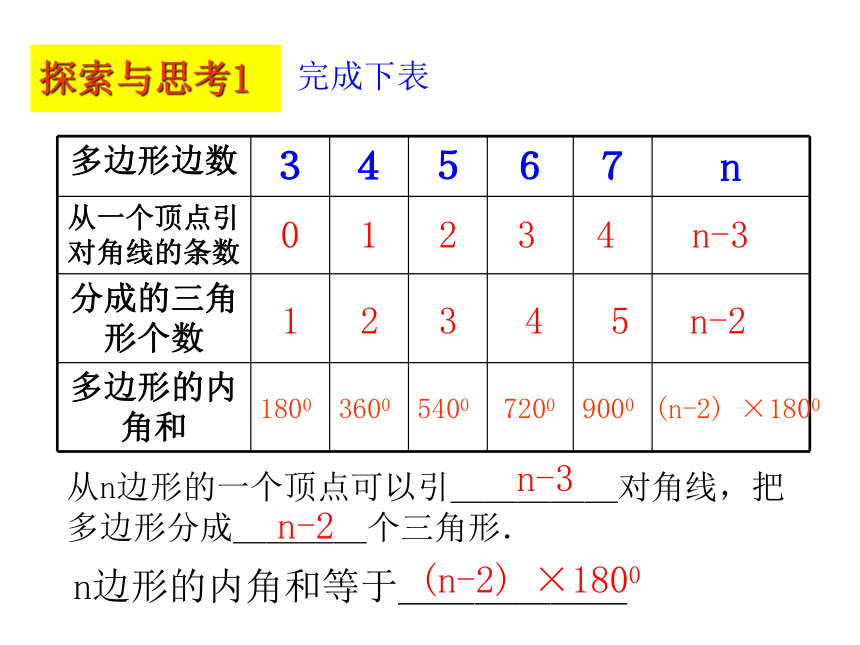
多边形边数 3 4 5 6 7 n
从一个顶点引对角线的条数
分成的三角形个数
多边形的内角和
n-2
4
3
2
1
0
5
4
3
2
1
n-3
1800
3600
5400
7200
9000
(n-2) ×1800
从n边形的一个顶点可以引_____对角线,把多边形分成____个三角形.
n边形的内角和等于______
n-3
n-2
(n-2) ×1800
探索与思考1
完成下表
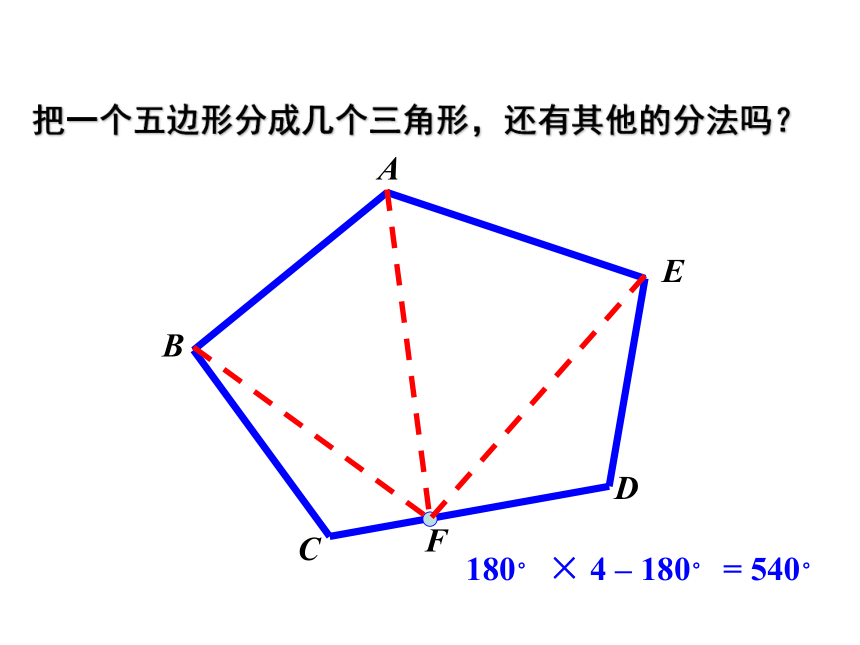
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180° × 4 – 180° = 540°
E
A
B
C
D
O
180°× 5 – 360°= 540°
A
B
C
D
E
4 × 180°-180 °
O
=540°
1. 求下列图形中 x 的值 .
(1)
(2)
速战速决
2x+140°+90°=360°
360°-80°-120°-75°=180°-x
x=65°
x=95°
(2)七边形的内角和等于______度.
2、填空题
900
(3)一个多边形的内角和等于1440°,那么这个多边形是______边形.
十
(1)多边形的内角和随着边数的增加而______,边数增加一条时,它的内角和增加________度 .
增加
180
(4)已知一个多边形每个内角都等于 108°,那么这个多边形是 边形.
五
(5) 正n边形每个内角的度数是___ __度 。
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:
如图,四边形ABCD中,
∠A+ ∠C =180°
∠A+∠B+∠C+∠D=(4-2) ×180 °
= 360 °
因为
∠B+∠D
= 360°-(∠A+∠C)
= 360°- 180°
=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
所以
例1 :
1.把一个五边形锯去一个内角后得到是什么图形?此时,多边形的内角和与外角和有什么变化?
①
②
③
解:五边形锯去一个内角后得到的图形可能是四边形,如图①;五边形,如图②;六边形,如图③
其内角和分别是360°,540°,720°。
是原来的多边形内角和度数本身,少180度和多180度
谁与争锋
解:假设这个多边形的边数是n,那个内角的度数为x
则有:(n-2) ·180=2750+x
因为n是正整数,所以2750+x也是180的倍数
因为x<180
所以x=130
所以(n-2) ·180=2880
所以n=18
2.已知一个多边形除了一个内角外,其余各内角的和是2750°,求这个多边形的边数。
小结
1、n(n≥3)边形的的内角和为(n-2)x180°
4、多边形的边数与内角和的关系
边数增加,内角和增加,边数减少,内角和减少,每增加一条边,内角和增加180°(反过来也成立),边数的内角和是180°的整数倍。
5、正n(n≥3)边形的的内角和为
作业 教材24页练习1、2、3.
新人教版 八年级(上) 数学 第11章
§11.3.2 多边形的内角和
(第一课时)
学习目标:
重点与难点:
1.知识目标:
了解多边形内角和公式以及运用公式进行有关计算。
2.能力目标:
(1)通过测量、类比、推理等数学活动,探索多边形内角和公式,感受数学思考过程中的条理性,发展推理能力和语言表达能力。
(2)通过把多边形转化为三角形体会转化思想在几何中的运用,同时让学生体会从特殊到一般的认识问题的方法。
重点
探索多边形内角和公式。
难点
探索多边形内角和时,如何把多边形转化为三角形
3.三角形的内角和是_____度.
2.在多边形中连接______________________的线段叫做多边形的对角线。
1.在平面内,___________________________叫做多边形。
由一些线段首尾顺次相接组成的图形
多边形不相邻的两个顶点
180
4.正方形的内角和是 度,长方形的内角和是 度。
360
360
知识回顾
A
B
C
D
任意一个四边形的内角和都等于360°
思路:把求四边形内角和的问题转化为三角形问题来解决!
想一想:一般的四边形的内角和是多少度呢?
1
3
2
4
五边形的内角和为540°
七边形的内角和为900°
六边形的内角和为720°
四边形、五边形、六边形、七边形从一个顶点出发分别可以引多少条对角线?分别把多边形分成多少个三角形?你能从中探索出规律吗?
试求五边形、六边形、七边形的内角和.
探索与思考1
多边形边数 3 4 5 6 7 n
从一个顶点引对角线的条数
分成的三角形个数
多边形的内角和
n-2
4
3
2
1
0
5
4
3
2
1
n-3
1800
3600
5400
7200
9000
(n-2) ×1800
从n边形的一个顶点可以引_____对角线,把多边形分成____个三角形.
n边形的内角和等于______
n-3
n-2
(n-2) ×1800
探索与思考1
完成下表
把一个五边形分成几个三角形,还有其他的分法吗?
A
B
C
D
E
F
180° × 4 – 180° = 540°
E
A
B
C
D
O
180°× 5 – 360°= 540°
A
B
C
D
E
4 × 180°-180 °
O
=540°
1. 求下列图形中 x 的值 .
(1)
(2)
速战速决
2x+140°+90°=360°
360°-80°-120°-75°=180°-x
x=65°
x=95°
(2)七边形的内角和等于______度.
2、填空题
900
(3)一个多边形的内角和等于1440°,那么这个多边形是______边形.
十
(1)多边形的内角和随着边数的增加而______,边数增加一条时,它的内角和增加________度 .
增加
180
(4)已知一个多边形每个内角都等于 108°,那么这个多边形是 边形.
五
(5) 正n边形每个内角的度数是___ __度 。
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:
如图,四边形ABCD中,
∠A+ ∠C =180°
∠A+∠B+∠C+∠D=(4-2) ×180 °
= 360 °
因为
∠B+∠D
= 360°-(∠A+∠C)
= 360°- 180°
=180°
这就是说:如果四边形一组对角互补,那么另一组对角也互补.
所以
例1 :
1.把一个五边形锯去一个内角后得到是什么图形?此时,多边形的内角和与外角和有什么变化?
①
②
③
解:五边形锯去一个内角后得到的图形可能是四边形,如图①;五边形,如图②;六边形,如图③
其内角和分别是360°,540°,720°。
是原来的多边形内角和度数本身,少180度和多180度
谁与争锋
解:假设这个多边形的边数是n,那个内角的度数为x
则有:(n-2) ·180=2750+x
因为n是正整数,所以2750+x也是180的倍数
因为x<180
所以x=130
所以(n-2) ·180=2880
所以n=18
2.已知一个多边形除了一个内角外,其余各内角的和是2750°,求这个多边形的边数。
小结
1、n(n≥3)边形的的内角和为(n-2)x180°
4、多边形的边数与内角和的关系
边数增加,内角和增加,边数减少,内角和减少,每增加一条边,内角和增加180°(反过来也成立),边数的内角和是180°的整数倍。
5、正n(n≥3)边形的的内角和为
作业 教材24页练习1、2、3.
