人教版数学八年级上册11.2.2 三角形的外角 课件(共19张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.2.2 三角形的外角 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 391.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
11.2.2 三角形的外角
11.2 与三角形有关的角
旧知回顾
【前言】上节课,我们已经学习了三角形的内角和定理的有关知识。
性质探究
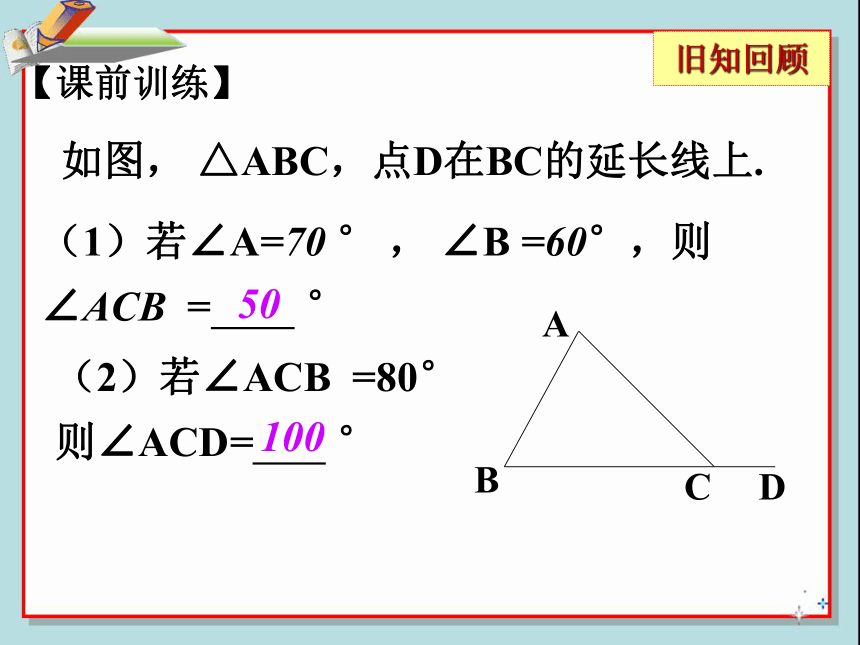
【课前训练】
(1)若∠A=70 ° , ∠B =60°,则
∠ACB = °
A
B
C
D
(2)若∠ACB =80°
则∠ACD= °
50
100
旧知回顾
如图, △ABC,点D在BC的延长线上.
新知引入
【引言】今天,让我们一起来学习三角形外角的定义、探究三角形外角的性质及其在实际问题中应用.
新知讲解
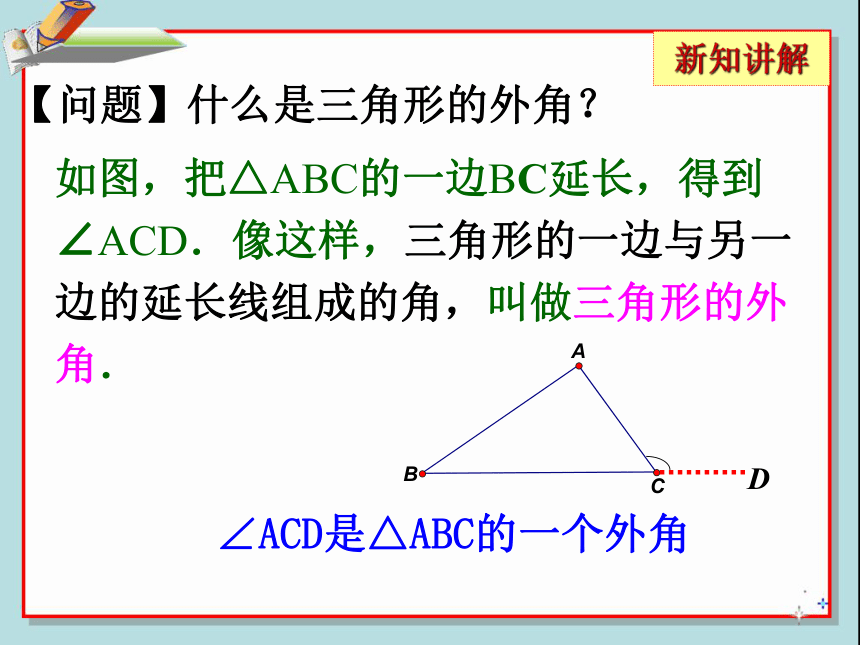
【问题】什么是三角形的外角?
如图,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
C
B
A
D
∠ACD是△ABC的一个外角
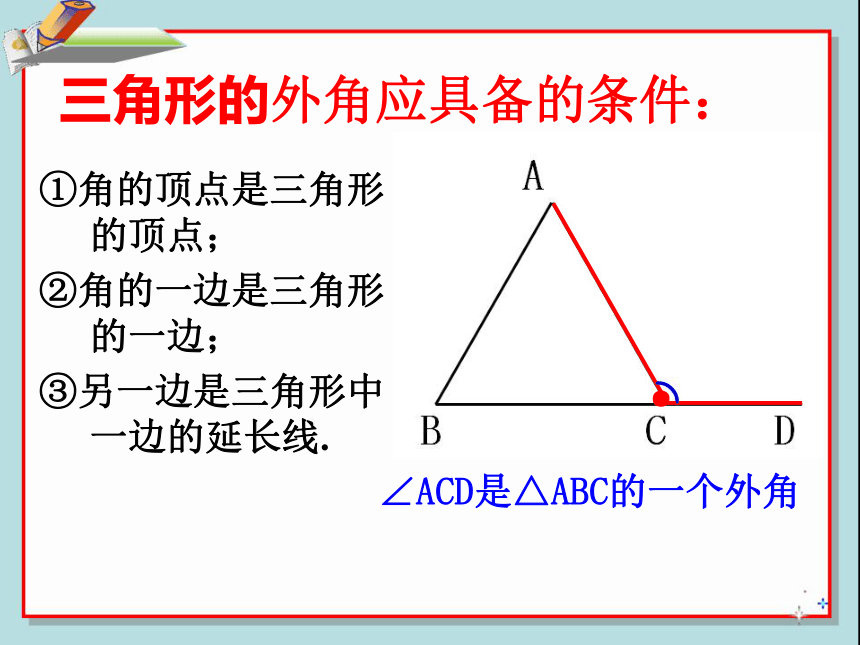
三角形的外角应具备的条件:
∠ACD是△ABC的一个外角
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
·
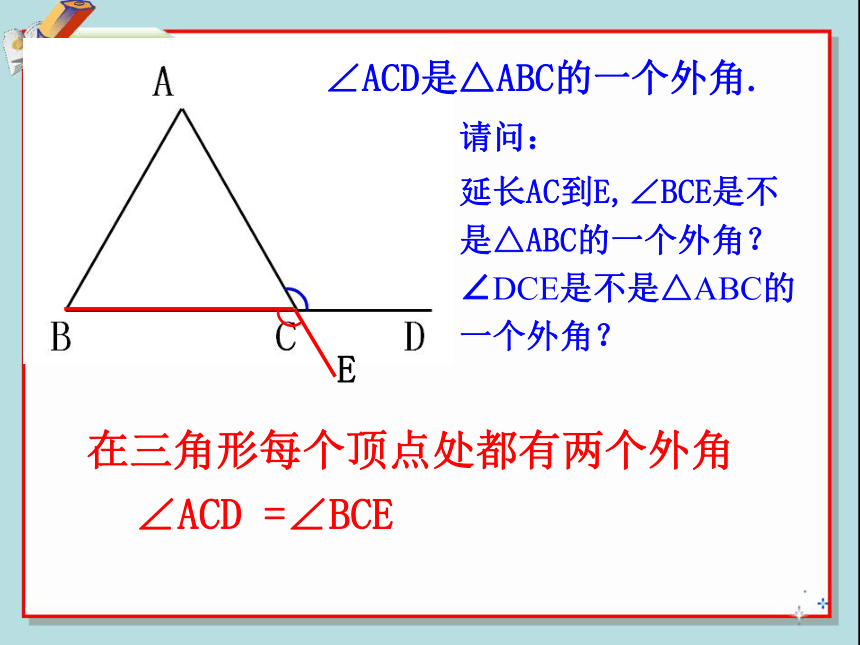
请问:
延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角
∠ACD是△ABC的一个外角.
∠ACD =∠BCE
A
B
C
1
2
3
4
5
6
一个三角形有6个外角,而且同一顶点处的两个外角是对顶角,他们是相等.
小露一手
【找外角】
1、∠BDC是哪个三角形的外角?
C
B
A
D
E
2、 ∠ACE是△ADC的外角吗?
性质探究
【三角形外角的性质】
三角形的外角等于与它不相邻的两个内角的和.
∠ACD=∠A+ ∠B
A
B
C
D
【练习】
1、如图,Rt△ABC中, ∠A=40 °,则∠ABD等于( )
A.110 ° B.120 °
C.130 ° D.140 °
A
B
C
D
C
学以致用
2、如图,△ABC中, ∠A=70 °,∠B=40 ° ,CE是△ABC外角∠ACD
的平分线,则∠ECD=( )
A.55 ° B.60 °
C.65 ° D.75 °
A
B
C
D
E
A
学以致用
3、如图,AB∥CD,∠A=45°,
∠C= ∠E,则∠C= .
答案:22.5 °
学以致用
P
4、如图,五角星的五个角∠A,∠B,∠C,∠D,∠E的度数之和等于______ ° .
答案:180
学以致用
【例】如图,∠BAE, ∠CBF, ∠ACD,
是△ABC的三个外角,它们的和是多少?
应用举例
【议】如图,△ABC,BF平分∠DBC,CF平分∠BCE .
(1)若∠A=40 °,则∠DBC+ ∠BCE= 度;
(2)各小组组长设定∠A的度数,小组合作求出∠F的度数.
A
B
E
C
D
F
拓展延伸
(3)猜想∠F与∠A的数
量关系,并证明你的结论
总结归纳
通过本节课的学习,你有什么收获?
1、什么是三角形的外角?
2、三角形的外角有什么性质?
三角形的一边与另一边的延长线组成的角
三角形的外角等于与它不相邻的两个内角的和.
布置作业
如图,△ABC,BP平分∠ABC,CP平分∠ACE ,记∠A=m度,试用m表示∠P的度数。
A
B
P
C
E
1、课本第15页练习题、17页第8题;
2、拓展练习:
作业:
11.2.2 三角形的外角
11.2 与三角形有关的角
旧知回顾
【前言】上节课,我们已经学习了三角形的内角和定理的有关知识。
性质探究
【课前训练】
(1)若∠A=70 ° , ∠B =60°,则
∠ACB = °
A
B
C
D
(2)若∠ACB =80°
则∠ACD= °
50
100
旧知回顾
如图, △ABC,点D在BC的延长线上.
新知引入
【引言】今天,让我们一起来学习三角形外角的定义、探究三角形外角的性质及其在实际问题中应用.
新知讲解
【问题】什么是三角形的外角?
如图,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
C
B
A
D
∠ACD是△ABC的一个外角
三角形的外角应具备的条件:
∠ACD是△ABC的一个外角
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
·
请问:
延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
E
在三角形每个顶点处都有两个外角
∠ACD是△ABC的一个外角.
∠ACD =∠BCE
A
B
C
1
2
3
4
5
6
一个三角形有6个外角,而且同一顶点处的两个外角是对顶角,他们是相等.
小露一手
【找外角】
1、∠BDC是哪个三角形的外角?
C
B
A
D
E
2、 ∠ACE是△ADC的外角吗?
性质探究
【三角形外角的性质】
三角形的外角等于与它不相邻的两个内角的和.
∠ACD=∠A+ ∠B
A
B
C
D
【练习】
1、如图,Rt△ABC中, ∠A=40 °,则∠ABD等于( )
A.110 ° B.120 °
C.130 ° D.140 °
A
B
C
D
C
学以致用
2、如图,△ABC中, ∠A=70 °,∠B=40 ° ,CE是△ABC外角∠ACD
的平分线,则∠ECD=( )
A.55 ° B.60 °
C.65 ° D.75 °
A
B
C
D
E
A
学以致用
3、如图,AB∥CD,∠A=45°,
∠C= ∠E,则∠C= .
答案:22.5 °
学以致用
P
4、如图,五角星的五个角∠A,∠B,∠C,∠D,∠E的度数之和等于______ ° .
答案:180
学以致用
【例】如图,∠BAE, ∠CBF, ∠ACD,
是△ABC的三个外角,它们的和是多少?
应用举例
【议】如图,△ABC,BF平分∠DBC,CF平分∠BCE .
(1)若∠A=40 °,则∠DBC+ ∠BCE= 度;
(2)各小组组长设定∠A的度数,小组合作求出∠F的度数.
A
B
E
C
D
F
拓展延伸
(3)猜想∠F与∠A的数
量关系,并证明你的结论
总结归纳
通过本节课的学习,你有什么收获?
1、什么是三角形的外角?
2、三角形的外角有什么性质?
三角形的一边与另一边的延长线组成的角
三角形的外角等于与它不相邻的两个内角的和.
布置作业
如图,△ABC,BP平分∠ABC,CP平分∠ACE ,记∠A=m度,试用m表示∠P的度数。
A
B
P
C
E
1、课本第15页练习题、17页第8题;
2、拓展练习:
作业:
