人教版数学八年级上册 12.1 全等三角形 课件(共20张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.1 全等三角形 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 15:15:13 | ||
图片预览






文档简介
(共20张PPT)
12.1 全等三角形
学习任务:
1.知道全等形,全等三角形的概念。
2. 学会全等三角形的表示方法及性质。
3.运用全等三角形的性质进行推理和计算.
观察
同一张底片洗出的同规格照片.
两张纸重合后的剪纸;
还有……?
举例
自主学习:
阅读教材31页探究,完成下列问题:
1.什么是全等形?
2.什么是全等三角形?
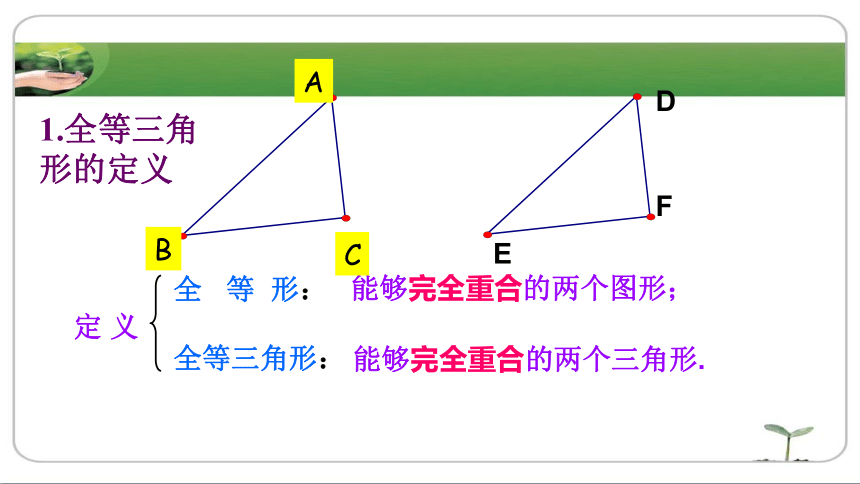
能够完全重合的两个图形;
全 等 形:
全等三角形:
定 义
能够完全重合的两个三角形.
A
B
C
D
F
E
1.全等三角形的定义
自主学习:
阅读教材32页第二自然段:
1.找出全等三角形的对应关系
2.全等三角形的表示方法
点A 与点D、点B 与点E、
点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、
边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、
∠C 与∠F 重合,称为对应角.
展示反馈1. 请同学们观察这两个三角形有何对应关系?
A
B
C
D
E
F
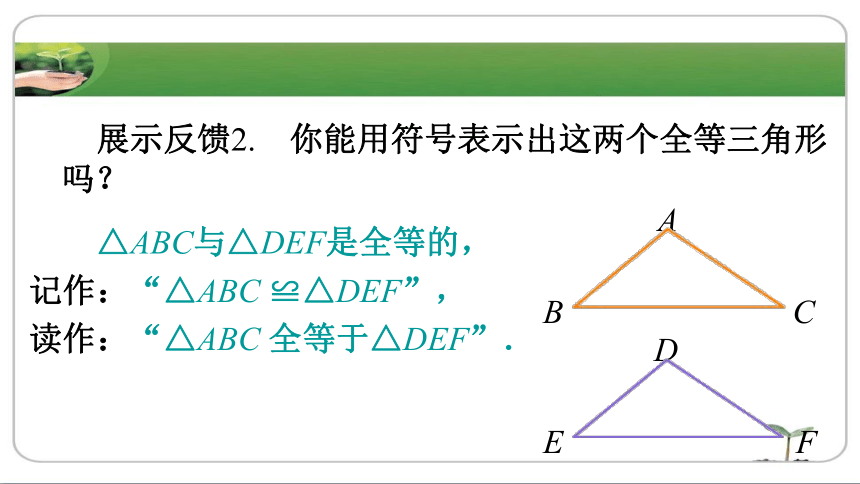
△ABC与△DEF是全等的,
记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”.
展示反馈2. 你能用符号表示出这两个全等三角形吗?
A
B
C
D
E
F
全等三角形的性质:
全等三角形的对应边相等、
对应角相等.
全等三角形的对应边和对应角有何大小关
系?
A
B
C
D
E
F
用几何语言表述:
∵ △ABC ≌△DEF,
∴ AB =DE,BC =EF,AC =DF
(全等三角形的对应边相等),
∠A =∠D,∠B =∠E,∠C =∠F
(全等三角形的对应角相等).
全等三角形的对应边和对应角有何大小关
系?
A
B
C
D
E
F
解:∵ ∠A =100°,∠B =30°,
∴ ∠C =180°-∠A -∠B
=50°.
∵ △DEF ≌△ABC ,
∴ ∠F =∠C =50°
(全等三角形的对应角相等).
例 已知:如图,△ABC ≌△DEF.
若∠A =100°,∠B =30°,求∠F 的度数.
A
B
C
D
E
F
A
B
C
D
E
O
1. △ABD≌△ACE,若∠B=25°, BD=6㎝, AD=4㎝, 你能得出△ACE中哪些角的大小,哪些边的长度吗?为什么 ?
展示反馈
平移、翻折、旋转形状、大小都不变
结论:平移、翻折、旋转前后的图形全等.
⑴平移
⑵翻折
⑶旋转
思考
A
B
O
C
D
A
B
C
D
A
B
C
D
A
B
C
D
E
全等对应元素的找法
寻找对应元素的规律
1. 有公共边的,公共边是对应边;
2. 有公共角的,公共角是对应角;
3. 有对顶角的,对顶角是对应角;
4. 两个全等三角形最大的边是对应边, 最小的边也是对应边;
5. 两个全等三角形最大的角是对应角, 最小的角也是对应角.
方法
如图,△EFG ≌△NMH,∠F 和∠M 是对
应角.
(1)FG 与MH 平行吗?为什么?
(2)判断线段EH 与NG 的大小关系,并说明理由.
(1)平行;
(2)相等.
H
E
N
G
F
M
检测提升
重点掌握:
明白道理:
“全等”和“对应相等”
因“完全重合”而“全等”
因“完全重合”而“对应”边(角)相等
这节课你学会了什么呢?
小结
有一种学习,
没有参与,
你不会知道精彩纷呈;
有一种交流,
没有融入,
你不会知道头脑风暴;
有一种苦累,
没有体会,
你不会知道收获快乐。
习题12.1中的1题2题
作业
12.1 全等三角形
学习任务:
1.知道全等形,全等三角形的概念。
2. 学会全等三角形的表示方法及性质。
3.运用全等三角形的性质进行推理和计算.
观察
同一张底片洗出的同规格照片.
两张纸重合后的剪纸;
还有……?
举例
自主学习:
阅读教材31页探究,完成下列问题:
1.什么是全等形?
2.什么是全等三角形?
能够完全重合的两个图形;
全 等 形:
全等三角形:
定 义
能够完全重合的两个三角形.
A
B
C
D
F
E
1.全等三角形的定义
自主学习:
阅读教材32页第二自然段:
1.找出全等三角形的对应关系
2.全等三角形的表示方法
点A 与点D、点B 与点E、
点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、
边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、
∠C 与∠F 重合,称为对应角.
展示反馈1. 请同学们观察这两个三角形有何对应关系?
A
B
C
D
E
F
△ABC与△DEF是全等的,
记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”.
展示反馈2. 你能用符号表示出这两个全等三角形吗?
A
B
C
D
E
F
全等三角形的性质:
全等三角形的对应边相等、
对应角相等.
全等三角形的对应边和对应角有何大小关
系?
A
B
C
D
E
F
用几何语言表述:
∵ △ABC ≌△DEF,
∴ AB =DE,BC =EF,AC =DF
(全等三角形的对应边相等),
∠A =∠D,∠B =∠E,∠C =∠F
(全等三角形的对应角相等).
全等三角形的对应边和对应角有何大小关
系?
A
B
C
D
E
F
解:∵ ∠A =100°,∠B =30°,
∴ ∠C =180°-∠A -∠B
=50°.
∵ △DEF ≌△ABC ,
∴ ∠F =∠C =50°
(全等三角形的对应角相等).
例 已知:如图,△ABC ≌△DEF.
若∠A =100°,∠B =30°,求∠F 的度数.
A
B
C
D
E
F
A
B
C
D
E
O
1. △ABD≌△ACE,若∠B=25°, BD=6㎝, AD=4㎝, 你能得出△ACE中哪些角的大小,哪些边的长度吗?为什么 ?
展示反馈
平移、翻折、旋转形状、大小都不变
结论:平移、翻折、旋转前后的图形全等.
⑴平移
⑵翻折
⑶旋转
思考
A
B
O
C
D
A
B
C
D
A
B
C
D
A
B
C
D
E
全等对应元素的找法
寻找对应元素的规律
1. 有公共边的,公共边是对应边;
2. 有公共角的,公共角是对应角;
3. 有对顶角的,对顶角是对应角;
4. 两个全等三角形最大的边是对应边, 最小的边也是对应边;
5. 两个全等三角形最大的角是对应角, 最小的角也是对应角.
方法
如图,△EFG ≌△NMH,∠F 和∠M 是对
应角.
(1)FG 与MH 平行吗?为什么?
(2)判断线段EH 与NG 的大小关系,并说明理由.
(1)平行;
(2)相等.
H
E
N
G
F
M
检测提升
重点掌握:
明白道理:
“全等”和“对应相等”
因“完全重合”而“全等”
因“完全重合”而“对应”边(角)相等
这节课你学会了什么呢?
小结
有一种学习,
没有参与,
你不会知道精彩纷呈;
有一种交流,
没有融入,
你不会知道头脑风暴;
有一种苦累,
没有体会,
你不会知道收获快乐。
习题12.1中的1题2题
作业
