人教版数学八年级上册11.1.2 三角形的高、中线与角平分线 课件(共36张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.1.2 三角形的高、中线与角平分线 课件(共36张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 15:25:52 | ||
图片预览





文档简介
(共36张PPT)
第十一章 三角形
11.1.2 三角形的高、中线与角平分线
A
B
C
F
G
A
B
C
.
.
.
┐
D
A
B
C
.
.
.
┐
D
A
B
C
.
.
.
E
A
B
C
.
.
.
F
A
B
C
.
.
.
┐
D
A
B
C
.
.
.
E
A
B
C
.
.
.
F
1
2
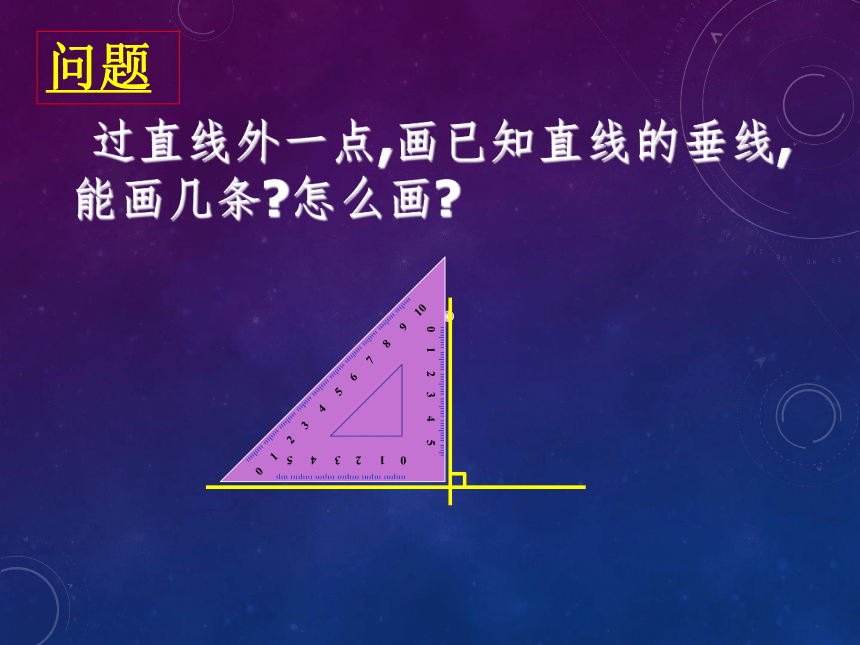
过直线外一点,画已知直线的垂线,能画几条 怎么画
问题
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
B
C
D
□
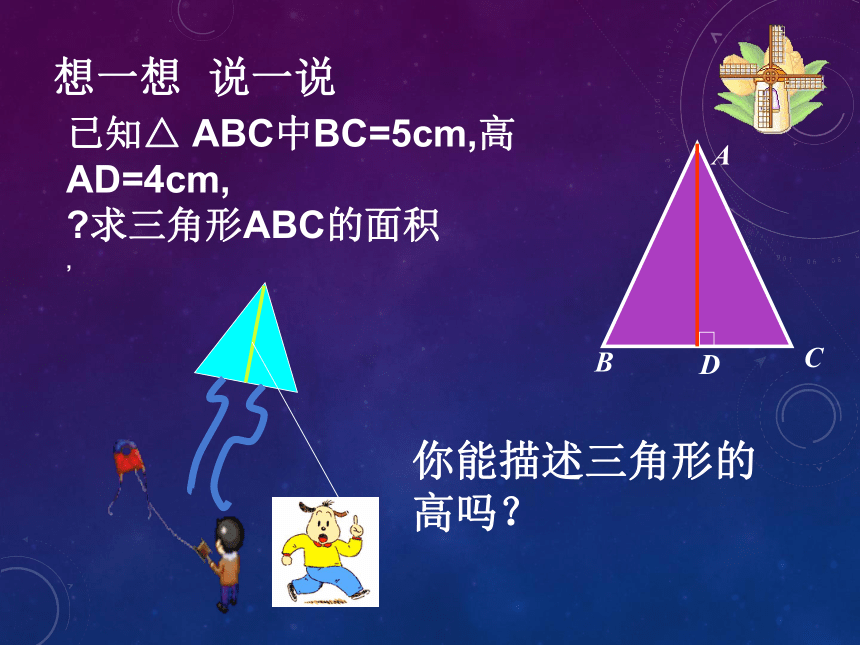
已知△ ABC中BC=5cm,高AD=4cm,
求三角形ABC的面积
,
你能描述三角形的高吗?
想一想 说一说
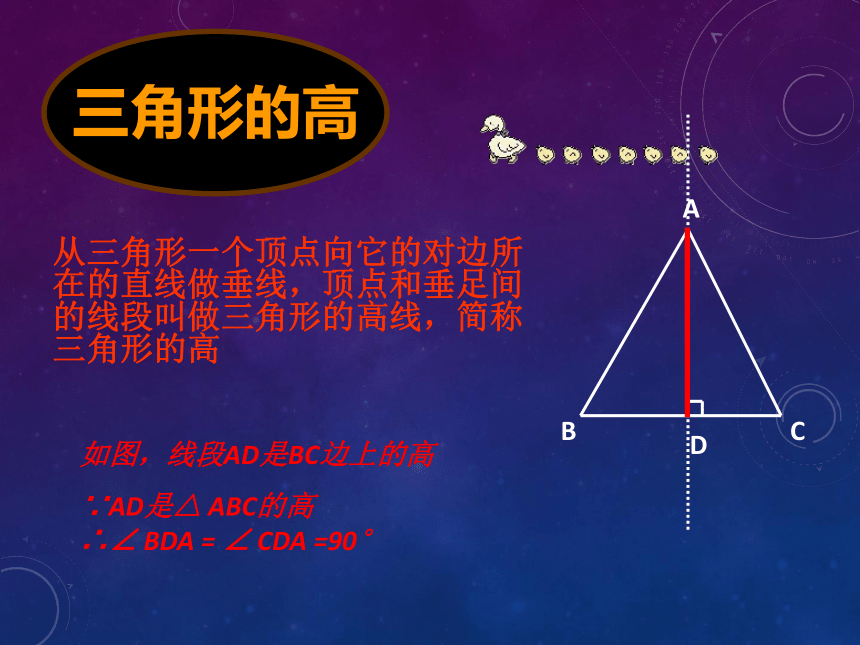
三角形的高
从三角形一个顶点向它的对边所在的直线做垂线,顶点和垂足间的线段叫做三角形的高线,简称三角形的高
A
B
C
D
如图,线段AD是BC边上的高
∵AD是△ ABC的高
∴∠ BDA = ∠ CDA =90°
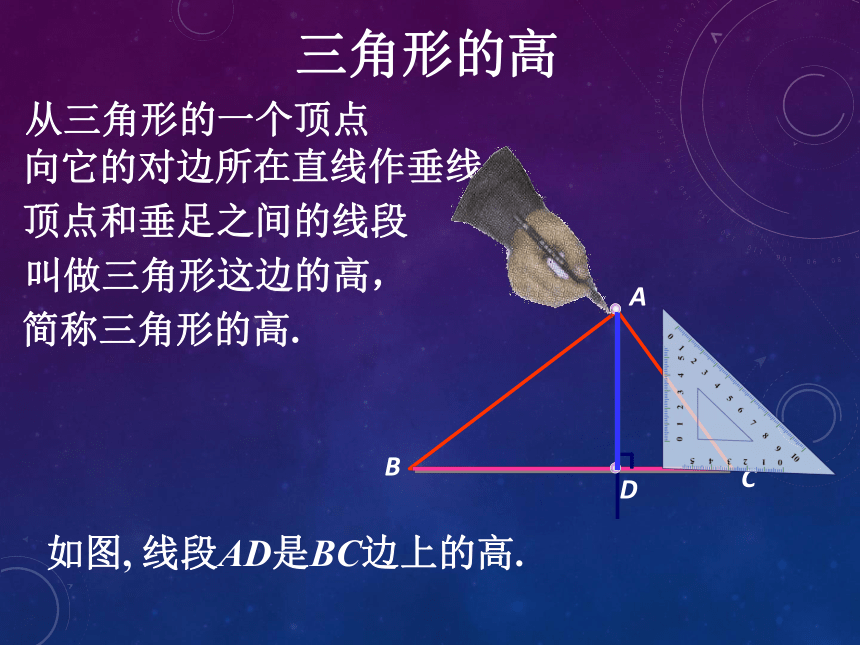
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形这边的高,
简称三角形的高.
如图, 线段AD是BC边上的高.
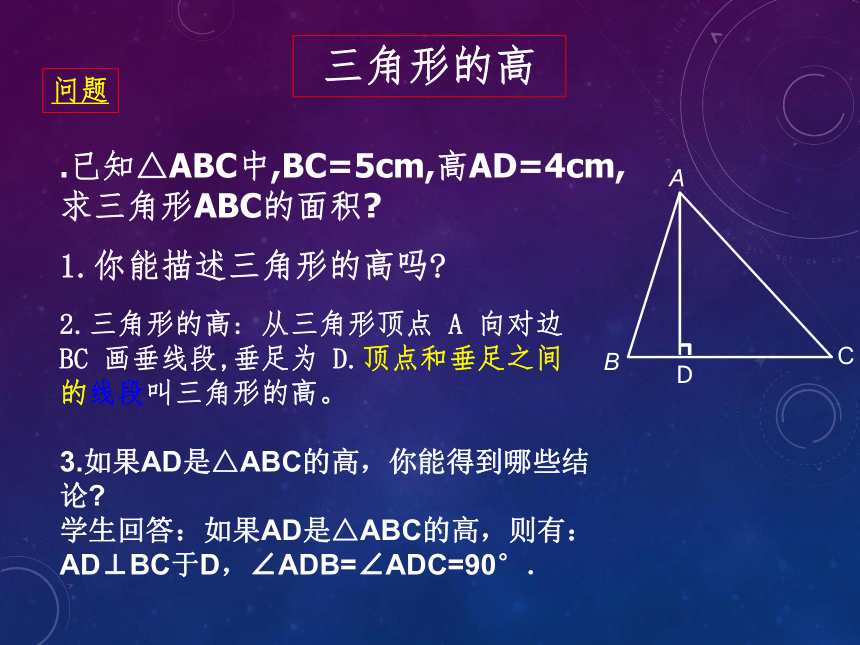
问题
.已知△ABC中,BC=5cm,高AD=4cm,
求三角形ABC的面积
B
A
C
D
1.你能描述三角形的高吗
2.三角形的高: 从三角形顶点 A 向对边 BC 画垂线段,垂足为 D.顶点和垂足之间的线段叫三角形的高。
3.如果AD是△ABC的高,你能得到哪些结论
学生回答:如果AD是△ABC的高,则有:AD⊥BC于D,∠ADB=∠ADC=90°.
三角形的高
一个三角形有几条高线 请折一折画一画
A
B
C
A
B
C
D
E
F
O
A
B
C
A
B
C
D
O
A
B
C
A
B
C
D
E
F
O
三角形的高
A
B
C
E
F
G
A
B
C
D
A
B
C
E
D
F
A
B
C
D
O
A
B
C
D
E
F
A
B
C
D
E
F
O
三角形的三条高的特性:
高有几条
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
3
3
3
三角形内部
直角顶点
三角形外部
高所在直线
练习
如果一个三角形的三条高的交点恰是三角形
的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上答案都对
B
C
练习1 在下图中,正确画出△ABC 中边BC 上高的
是( ).
( A ) ( B )
( C) ( D )
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
小试身手
问题1:如图,如果点C是线段AB的中点,你能得到什么结论
A
B
C
二、探索三角形的中线
三角形的中线
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边上的中线。
A
B
C
D
因为AD是△ABC的中线
所以BD=CD=
1
2
BC
任意画一个三角形,然后利用刻度尺画出这个三角形三条边的中线,你发现了什么?
●
●
E
F
O
三角形的三条中线相交于一点,交点在三角形的内部。
三角形的三条中线的交点,叫做三角形的重心。
三角形的中线
1.三角形的中线:
在三角形中,连接一个顶点与它对边中点的线段,
叫做这个三角形的中线.
2.一个三角形有几条中线
在三角形的内部还是外部
有交点吗
若有交点在什么位置
A
B
C
D
中线有几条
中线之间是否相交
若相交交点位置
中线在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
中线有几条
中线之间是否相交
若相交交点位置
中线在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
3
3
相交
相交
相交
3
3
3
三角形内部
三角形内部
三角形内部
A
B
C
D
E
F
O
三角形三条中线的交点叫做三角形的重心
如图在△ABC中,AD是BC 边上的中线
猜想:△ABD的面积和△ADC的面积有什么关系.试说明.
A
B
C
D
E
发挥想象
有一块三角形的 草地,要把它平均分给四个牧民,且每个牧民所分的草地都是三角形。请你探究出几种不同的 分法。
答:
△ABD和△ACD的面积相等.理由:
∵AD是△ABC的中线
∴BD=CD
∵AE既是△ABD的高,也是△ACD的高
∴△ABD和△ACD的面积相等.
问题5:通过问题4你能发现什么规律
三角形的中线将三角形的面积平均分成两份
问题6:有一块三角形的 草地,要把它平均分给四个牧民,且每个牧民所分的草地都是三角形。请你探究出几种不同的 分法。
三.通过类比的方法探究三角形的角平分线
1.画一个角的平分线.
A
B
O
C
问题1:如图,若OC是∠AOB的平分线,你能得
到什么结论
三角形的角平分线
2.三角形的角平分线
A
B
C
D
●
●
︶
︶
1
2
过一个顶点的角平分线与对边
交于一点,顶点与交点之间的线段
叫三角形的角平分线
∵AD是 △ ABC的角平分线
∴∠BAD = ∠CAD =
1
2
∠BAC
三角形的角平分线
一个三角形有几条角平分线
它们在三角形的内部还是外部
它们有交点吗 若有交点在什么位置
有几条
是否相交
若相交交点位置
在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
三角形的角平分线
3
3
3
相交
相交
相交
3
3
3
三角形内部
三角形内部
三角形内部
如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.
当∠A=40°时,求∠BOC的度数
解:
∵BD、CE分别是△ABC的角平分线
四、反思总结 情意发展
问题1:本节课你学习了什么
问题2:本节课你有哪些收获
问题3:通过今天的学习,你想进一步探究的问题是什么
五、思考与总结
1.本节主要学习三角形的高、中线和角平分的概念与性质.
2.本节涉及到的思想方法是类比思想.
3.注意的问题:
(1)每个三角形都有三条高,三条中线和三条角平分线.
(2)三角形的三条高交于一点,但锐角三角形的高交于三角形内一点,直角三角形的高交于直角的顶点,钝角三角形的高交于三角形外一点.三角形的三条中线交于三角形内一点,三角形的三条角平分线也交于三角形内的一点.
(3)三角形的高、中线和角平分线都是线段.
(4)能将三角形的面积平均分成两部分的线是三角形的中线.
第十一章 三角形
11.1.2 三角形的高、中线与角平分线
A
B
C
F
G
A
B
C
.
.
.
┐
D
A
B
C
.
.
.
┐
D
A
B
C
.
.
.
E
A
B
C
.
.
.
F
A
B
C
.
.
.
┐
D
A
B
C
.
.
.
E
A
B
C
.
.
.
F
1
2
过直线外一点,画已知直线的垂线,能画几条 怎么画
问题
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
B
C
D
□
已知△ ABC中BC=5cm,高AD=4cm,
求三角形ABC的面积
,
你能描述三角形的高吗?
想一想 说一说
三角形的高
从三角形一个顶点向它的对边所在的直线做垂线,顶点和垂足间的线段叫做三角形的高线,简称三角形的高
A
B
C
D
如图,线段AD是BC边上的高
∵AD是△ ABC的高
∴∠ BDA = ∠ CDA =90°
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形这边的高,
简称三角形的高.
如图, 线段AD是BC边上的高.
问题
.已知△ABC中,BC=5cm,高AD=4cm,
求三角形ABC的面积
B
A
C
D
1.你能描述三角形的高吗
2.三角形的高: 从三角形顶点 A 向对边 BC 画垂线段,垂足为 D.顶点和垂足之间的线段叫三角形的高。
3.如果AD是△ABC的高,你能得到哪些结论
学生回答:如果AD是△ABC的高,则有:AD⊥BC于D,∠ADB=∠ADC=90°.
三角形的高
一个三角形有几条高线 请折一折画一画
A
B
C
A
B
C
D
E
F
O
A
B
C
A
B
C
D
O
A
B
C
A
B
C
D
E
F
O
三角形的高
A
B
C
E
F
G
A
B
C
D
A
B
C
E
D
F
A
B
C
D
O
A
B
C
D
E
F
A
B
C
D
E
F
O
三角形的三条高的特性:
高有几条
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
3
3
3
三角形内部
直角顶点
三角形外部
高所在直线
练习
如果一个三角形的三条高的交点恰是三角形
的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.以上答案都对
B
C
练习1 在下图中,正确画出△ABC 中边BC 上高的
是( ).
( A ) ( B )
( C) ( D )
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
小试身手
问题1:如图,如果点C是线段AB的中点,你能得到什么结论
A
B
C
二、探索三角形的中线
三角形的中线
在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边上的中线。
A
B
C
D
因为AD是△ABC的中线
所以BD=CD=
1
2
BC
任意画一个三角形,然后利用刻度尺画出这个三角形三条边的中线,你发现了什么?
●
●
E
F
O
三角形的三条中线相交于一点,交点在三角形的内部。
三角形的三条中线的交点,叫做三角形的重心。
三角形的中线
1.三角形的中线:
在三角形中,连接一个顶点与它对边中点的线段,
叫做这个三角形的中线.
2.一个三角形有几条中线
在三角形的内部还是外部
有交点吗
若有交点在什么位置
A
B
C
D
中线有几条
中线之间是否相交
若相交交点位置
中线在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
中线有几条
中线之间是否相交
若相交交点位置
中线在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
3
3
相交
相交
相交
3
3
3
三角形内部
三角形内部
三角形内部
A
B
C
D
E
F
O
三角形三条中线的交点叫做三角形的重心
如图在△ABC中,AD是BC 边上的中线
猜想:△ABD的面积和△ADC的面积有什么关系.试说明.
A
B
C
D
E
发挥想象
有一块三角形的 草地,要把它平均分给四个牧民,且每个牧民所分的草地都是三角形。请你探究出几种不同的 分法。
答:
△ABD和△ACD的面积相等.理由:
∵AD是△ABC的中线
∴BD=CD
∵AE既是△ABD的高,也是△ACD的高
∴△ABD和△ACD的面积相等.
问题5:通过问题4你能发现什么规律
三角形的中线将三角形的面积平均分成两份
问题6:有一块三角形的 草地,要把它平均分给四个牧民,且每个牧民所分的草地都是三角形。请你探究出几种不同的 分法。
三.通过类比的方法探究三角形的角平分线
1.画一个角的平分线.
A
B
O
C
问题1:如图,若OC是∠AOB的平分线,你能得
到什么结论
三角形的角平分线
2.三角形的角平分线
A
B
C
D
●
●
︶
︶
1
2
过一个顶点的角平分线与对边
交于一点,顶点与交点之间的线段
叫三角形的角平分线
∵AD是 △ ABC的角平分线
∴∠BAD = ∠CAD =
1
2
∠BAC
三角形的角平分线
一个三角形有几条角平分线
它们在三角形的内部还是外部
它们有交点吗 若有交点在什么位置
有几条
是否相交
若相交交点位置
在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
三角形的角平分线
3
3
3
相交
相交
相交
3
3
3
三角形内部
三角形内部
三角形内部
如图,已知:△ABC中,BD、CE分别是△ABC的两条角平分线,相交于点O.
当∠A=40°时,求∠BOC的度数
解:
∵BD、CE分别是△ABC的角平分线
四、反思总结 情意发展
问题1:本节课你学习了什么
问题2:本节课你有哪些收获
问题3:通过今天的学习,你想进一步探究的问题是什么
五、思考与总结
1.本节主要学习三角形的高、中线和角平分的概念与性质.
2.本节涉及到的思想方法是类比思想.
3.注意的问题:
(1)每个三角形都有三条高,三条中线和三条角平分线.
(2)三角形的三条高交于一点,但锐角三角形的高交于三角形内一点,直角三角形的高交于直角的顶点,钝角三角形的高交于三角形外一点.三角形的三条中线交于三角形内一点,三角形的三条角平分线也交于三角形内的一点.
(3)三角形的高、中线和角平分线都是线段.
(4)能将三角形的面积平均分成两部分的线是三角形的中线.
