人教版数学八年级上册 12.2三角形全等的判定(三) 课件(共19张PPT)
文档属性
| 名称 | 人教版数学八年级上册 12.2三角形全等的判定(三) 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览

文档简介
(共19张PPT)
§12.2 三角形全等的判定(三)
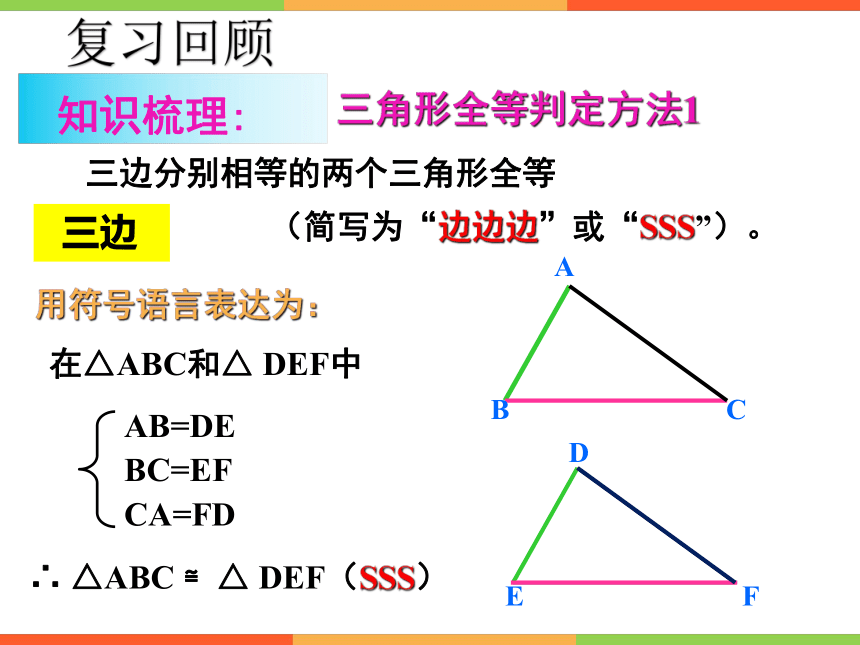
三边分别相等的两个三角形全等
(简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
知识梳理:
三边
复习回顾
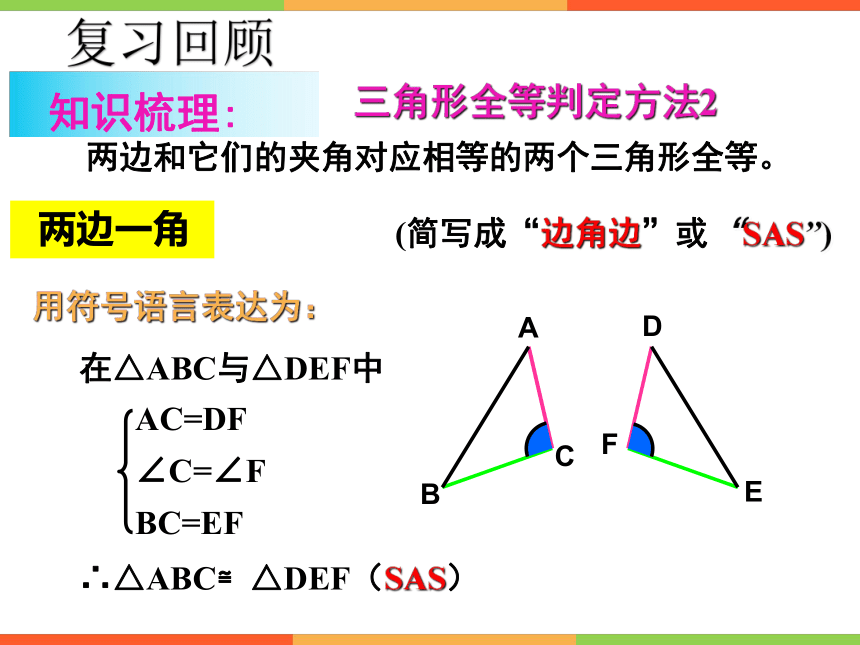
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。
(简写成“边角边”或“SAS”)
知识梳理:
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
两边一角
复习回顾
知识梳理:
A
B
D
A
B
C
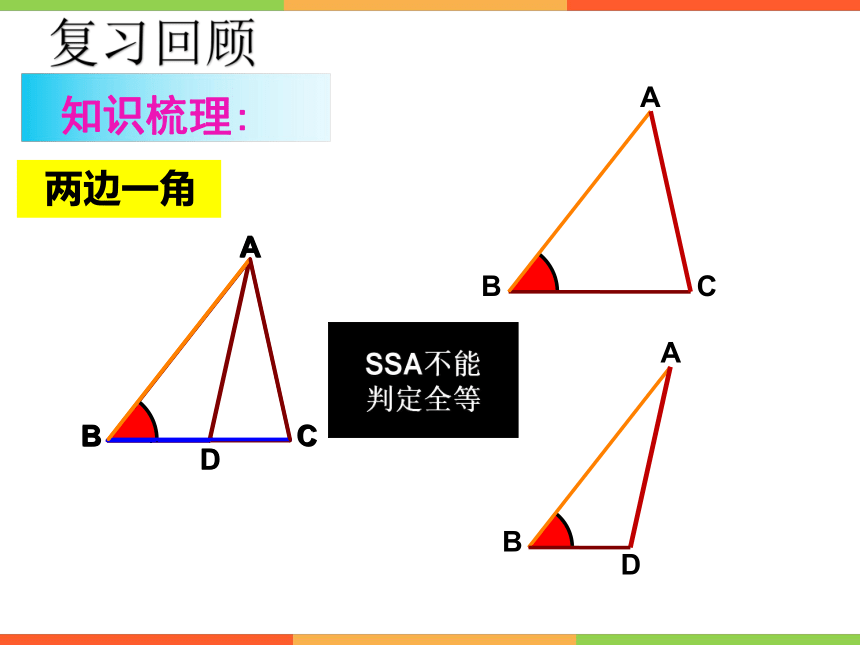
SSA不能判定全等
两边一角
复习回顾
继续探讨三角形全等的条件:
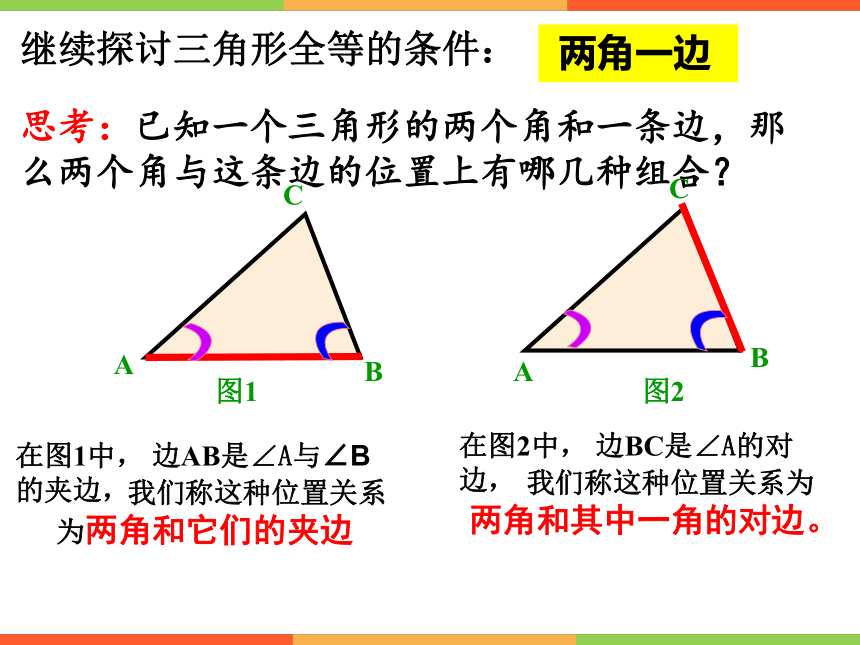
两角一边
思考:已知一个三角形的两个角和一条边,那么两个角与这条边的位置上有哪几种组合?
C
A
B
C
A
B
图1
图2
在图1中, 边AB是∠A与∠B的夹边,
在图2中, 边BC是∠A的对边,
我们称这种位置关系为两角和它们的夹边
我们称这种位置关系为两角和其中一角的对边。
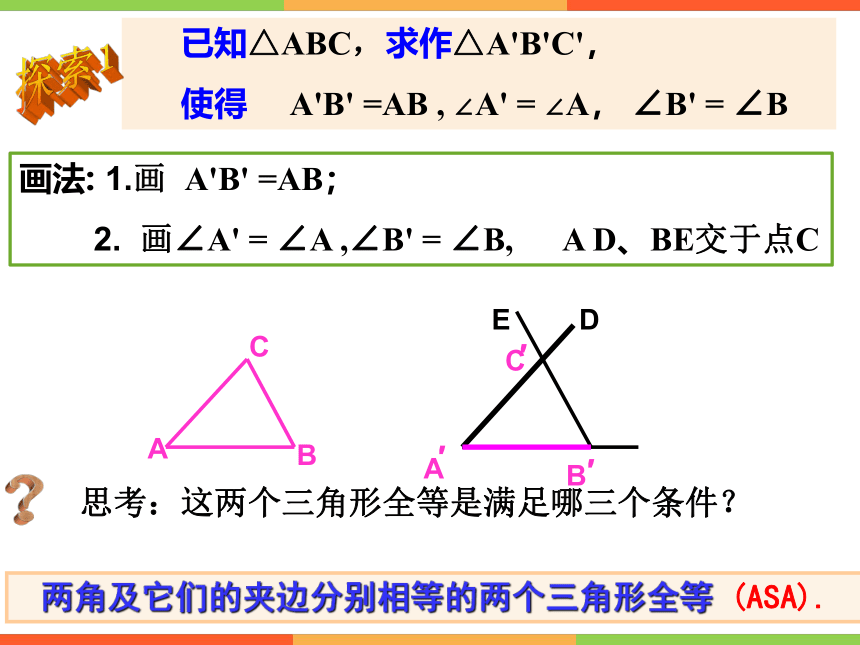
已知△ABC,求作△A'B'C',
使得 A'B' =AB , ∠A' = ∠A, ∠B' = ∠B
两角及它们的夹边分别相等的两个三角形全等 (ASA).
画法: 1.画 A'B' =AB;
2. 画∠A' = ∠A ,∠B' = ∠B, A D、BE交于点C
A
C
B
A
′
E
D
C
B
′
′
思考:这两个三角形全等是满足哪三个条件?
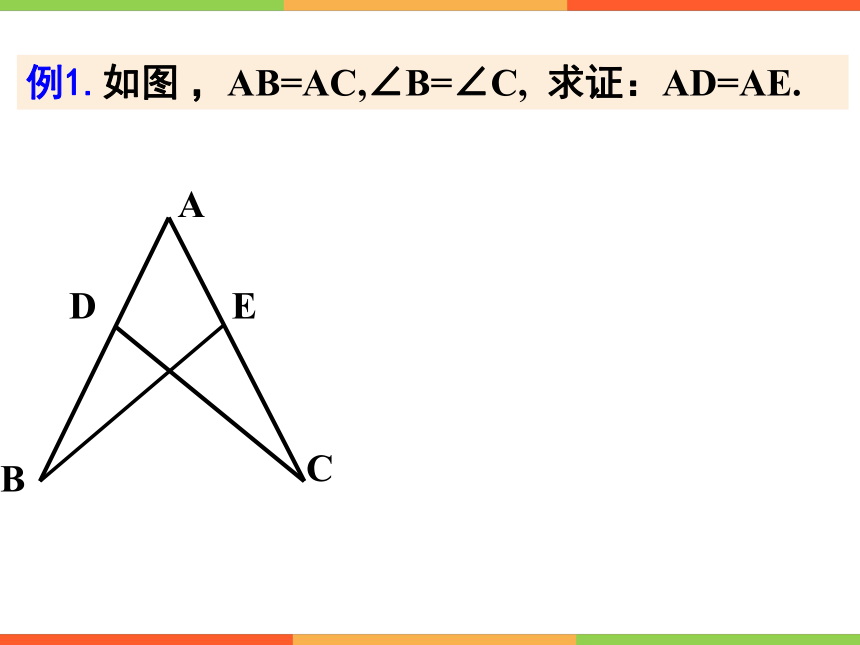
例1.如图 ,AB=AC,∠B=∠C, 求证:AD=AE.
A
E
D
C
B
例1.如图 ,AB=AC,∠B=∠C, 求证:AD=AE.
证明: 在△ACD与△ABE中
∠C=∠B
AC=AB
∠A= ∠A
∴ △ACD ≌△ABE (ASA)
A
E
D
C
B
∴
AD=AE
A
C
B
E
D
F
例2.如图 ,在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, 求证△ABC≌和△DEF.
A
C
B
E
D
F
证明:在△ABC中,∠C=180-∠A-∠B
在△ABC中,∠C=180-∠D-∠E
又 ∠A=∠D, ∠B=∠E
∴∠C=∠F
∠B=∠E
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
你能从上题中得到什么结论?
例2.如图 ,在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, 求证△ABC≌和△DEF.
在△ABC和△DEF中
两角及一角的对边对应相等的两个三角形全等 (AAS).
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。
两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”
(ASA)
(AAS)
归纳
练习1. 如图,AD和BC相交于点O,∠A=∠C
添加一个条件 ,使得AB=CD,请说明理由.
C
O
A
B
D
练习1. 如图,AD和BC相交于点O,∠A=∠C
添加一个条件 ,使得AB=CD,请说明理由.
C
O
A
B
D
法一: AO=CO
ASA
练习1. 如图,AD和BC相交于点O,∠A=∠C
添加一个条件 ,使得AB=CD,请说明理由.
C
O
A
B
D
法二: BO=DO
AAS
练习1. 如图,AD和BC相交于点O,∠A=∠C
添加一个条件 ,使得AB=CD,请说明理由.
C
O
A
B
D
法二: BO=DO
法一: AO=CO
ASA
AAS
A
B
C
D
E
F
练习2. 如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABC≌△DEF
A
B
C
D
E
F
证明:∵ BE=CF
∴BC=EF
∠B=∠E
在△ABC和△DEF中
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
∵ AB∥DE AC∥DF
∴ ∠B=∠DEF , ∠ACB=∠F
练习2. 如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABC≌△DEF
∴BE+EC=CF+EC
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识梳理:
(3)探索三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径。
数学思想:
分类,转化,猜想——验证
ASA AAS 引入
三条件
情境
ASA AAS 探究
实验法
推理证明
ASA AAS 运用
2个例题讲解
3练习巩固
综合归纳
ASA AAS 小结
知识梳理
数学思想
§12.2 三角形全等的判定(三)
三边分别相等的两个三角形全等
(简写为“边边边”或“SSS”)。
A
B
C
D
E
F
在△ABC和△ DEF中
∴ △ABC ≌△ DEF(SSS)
AB=DE
BC=EF
CA=FD
用符号语言表达为:
三角形全等判定方法1
知识梳理:
三边
复习回顾
三角形全等判定方法2
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS)
两边和它们的夹角对应相等的两个三角形全等。
(简写成“边角边”或“SAS”)
知识梳理:
F
E
D
C
B
A
AC=DF
∠C=∠F
BC=EF
两边一角
复习回顾
知识梳理:
A
B
D
A
B
C
SSA不能判定全等
两边一角
复习回顾
继续探讨三角形全等的条件:
两角一边
思考:已知一个三角形的两个角和一条边,那么两个角与这条边的位置上有哪几种组合?
C
A
B
C
A
B
图1
图2
在图1中, 边AB是∠A与∠B的夹边,
在图2中, 边BC是∠A的对边,
我们称这种位置关系为两角和它们的夹边
我们称这种位置关系为两角和其中一角的对边。
已知△ABC,求作△A'B'C',
使得 A'B' =AB , ∠A' = ∠A, ∠B' = ∠B
两角及它们的夹边分别相等的两个三角形全等 (ASA).
画法: 1.画 A'B' =AB;
2. 画∠A' = ∠A ,∠B' = ∠B, A D、BE交于点C
A
C
B
A
′
E
D
C
B
′
′
思考:这两个三角形全等是满足哪三个条件?
例1.如图 ,AB=AC,∠B=∠C, 求证:AD=AE.
A
E
D
C
B
例1.如图 ,AB=AC,∠B=∠C, 求证:AD=AE.
证明: 在△ACD与△ABE中
∠C=∠B
AC=AB
∠A= ∠A
∴ △ACD ≌△ABE (ASA)
A
E
D
C
B
∴
AD=AE
A
C
B
E
D
F
例2.如图 ,在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, 求证△ABC≌和△DEF.
A
C
B
E
D
F
证明:在△ABC中,∠C=180-∠A-∠B
在△ABC中,∠C=180-∠D-∠E
又 ∠A=∠D, ∠B=∠E
∴∠C=∠F
∠B=∠E
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
你能从上题中得到什么结论?
例2.如图 ,在△ABC和△DEF中, ∠A=∠D, ∠B=∠E,BC=EF, 求证△ABC≌和△DEF.
在△ABC和△DEF中
两角及一角的对边对应相等的两个三角形全等 (AAS).
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。
两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”
(ASA)
(AAS)
归纳
练习1. 如图,AD和BC相交于点O,∠A=∠C
添加一个条件 ,使得AB=CD,请说明理由.
C
O
A
B
D
练习1. 如图,AD和BC相交于点O,∠A=∠C
添加一个条件 ,使得AB=CD,请说明理由.
C
O
A
B
D
法一: AO=CO
ASA
练习1. 如图,AD和BC相交于点O,∠A=∠C
添加一个条件 ,使得AB=CD,请说明理由.
C
O
A
B
D
法二: BO=DO
AAS
练习1. 如图,AD和BC相交于点O,∠A=∠C
添加一个条件 ,使得AB=CD,请说明理由.
C
O
A
B
D
法二: BO=DO
法一: AO=CO
ASA
AAS
A
B
C
D
E
F
练习2. 如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABC≌△DEF
A
B
C
D
E
F
证明:∵ BE=CF
∴BC=EF
∠B=∠E
在△ABC和△DEF中
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
∵ AB∥DE AC∥DF
∴ ∠B=∠DEF , ∠ACB=∠F
练习2. 如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABC≌△DEF
∴BE+EC=CF+EC
(1) 两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”.
(2) 两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
知识梳理:
(3)探索三角形全等是证明线段相等(对应边相等),
角相等(对应角相等)等问题的基本途径。
数学思想:
分类,转化,猜想——验证
ASA AAS 引入
三条件
情境
ASA AAS 探究
实验法
推理证明
ASA AAS 运用
2个例题讲解
3练习巩固
综合归纳
ASA AAS 小结
知识梳理
数学思想
