28.1 锐角三角函数(3)--特殊角的三角函数值
文档属性
| 名称 | 28.1 锐角三角函数(3)--特殊角的三角函数值 |  | |
| 格式 | zip | ||
| 文件大小 | 99.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-31 11:36:35 | ||
图片预览





文档简介
课件14张PPT。28.1 锐角三角函数(3)——特殊角的三角函数值复习回顾1、锐角三角函数的定义在Rt△ABC中,∠C=90°,
(1)∠A的正弦sinA= 。(2)∠A的余弦cosA= 。(3)∠A的正切tanA= 。锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。2、互余两角的三角函数性质在Rt△ABC中,当∠C=90°,
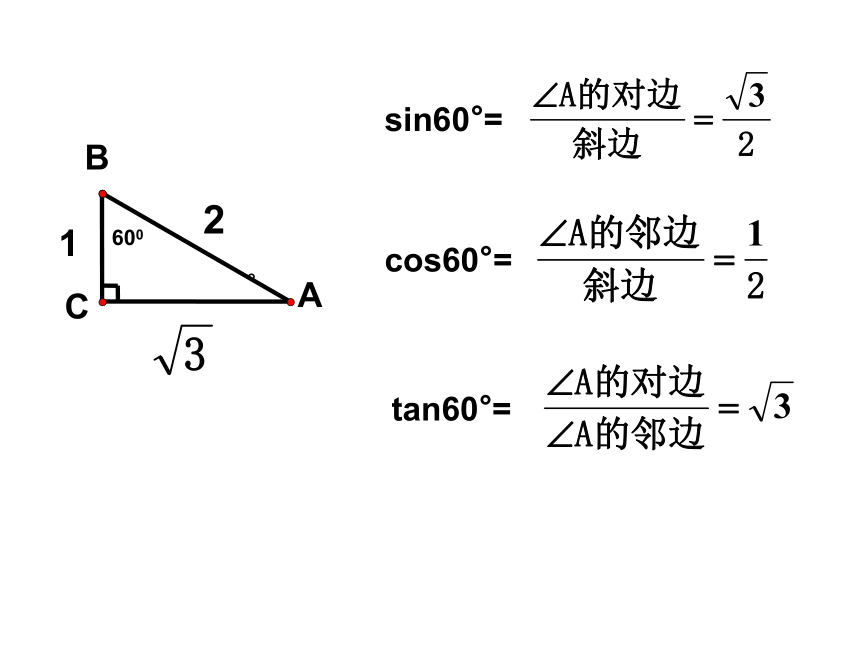
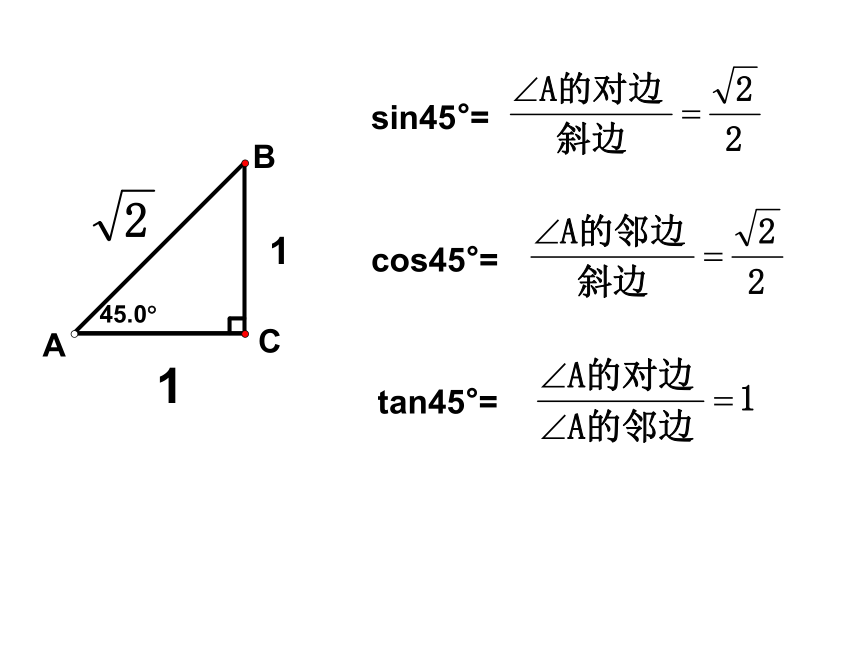
则有sinA= ,cosA= ,tanA.tanB= .cosBsinB1【探究】一副三角尺有几个不同的锐角?你能求出这几个锐角的正弦值、余弦值和正切值吗?新知探索:sin30°=cos30°=tan30°=sin60°=cos60°=tan60°=cos45°=tan45°=sin45°=列表如下:仔细观察表格,你有什么发现?α 的正弦值随着角度的增大而增大, α 的余弦值随着角度的增大而减少, α 的正切值随着角度的增大而增大。当 0°<α<90°时,且0 <sinα< 1,0 <cosα< 1例1.计算: (1)cos260°+sin260 ° 【应用新知】练习1:当锐角α>30°,则cosα的值 ( )例2、(1)如图,在Rt△ABC中,∠C=90°,AB= , BC= 。求∠A的度数。(1)(2) (2)如图,已知圆锥的高AO等于圆锥的底面半径OB的 倍,求α. 例3.求适合下列各式的锐角α练习2:【迁移拓展】┏D练习3: 如图,平地上一棵树高5m,两次观察它在地面上的影子,第一次是当阳光与地面成45°时,第二次是当阳光与地面成30°时,问第二次观察到的影子比第一次长多少米?1、特殊角三角函数值:2、三角函数的性质:α的正弦值随着角度的增大而增大, α的余弦值随着角度的增大而减少, α的正切值随着角度的增大而增大。当 0° <α< 90°时且0 <sinα< 1,0 <cosα< 1小 结:4、通过三角函数值可以把边和角有机地联系在一起,由边求角,由角求边。3、三角函数值和角之间是对应的,知道三角函数值可以求角的度数,知道角的度数可以求出三角函数值。今天作业:1 作业本(1) P20---21 作业本(2) P19---202 课时作业本P80---81
(1)∠A的正弦sinA= 。(2)∠A的余弦cosA= 。(3)∠A的正切tanA= 。锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。2、互余两角的三角函数性质在Rt△ABC中,当∠C=90°,
则有sinA= ,cosA= ,tanA.tanB= .cosBsinB1【探究】一副三角尺有几个不同的锐角?你能求出这几个锐角的正弦值、余弦值和正切值吗?新知探索:sin30°=cos30°=tan30°=sin60°=cos60°=tan60°=cos45°=tan45°=sin45°=列表如下:仔细观察表格,你有什么发现?α 的正弦值随着角度的增大而增大, α 的余弦值随着角度的增大而减少, α 的正切值随着角度的增大而增大。当 0°<α<90°时,且0 <sinα< 1,0 <cosα< 1例1.计算: (1)cos260°+sin260 ° 【应用新知】练习1:当锐角α>30°,则cosα的值 ( )例2、(1)如图,在Rt△ABC中,∠C=90°,AB= , BC= 。求∠A的度数。(1)(2) (2)如图,已知圆锥的高AO等于圆锥的底面半径OB的 倍,求α. 例3.求适合下列各式的锐角α练习2:【迁移拓展】┏D练习3: 如图,平地上一棵树高5m,两次观察它在地面上的影子,第一次是当阳光与地面成45°时,第二次是当阳光与地面成30°时,问第二次观察到的影子比第一次长多少米?1、特殊角三角函数值:2、三角函数的性质:α的正弦值随着角度的增大而增大, α的余弦值随着角度的增大而减少, α的正切值随着角度的增大而增大。当 0° <α< 90°时且0 <sinα< 1,0 <cosα< 1小 结:4、通过三角函数值可以把边和角有机地联系在一起,由边求角,由角求边。3、三角函数值和角之间是对应的,知道三角函数值可以求角的度数,知道角的度数可以求出三角函数值。今天作业:1 作业本(1) P20---21 作业本(2) P19---202 课时作业本P80---81
