28.1 锐角三角函数(4)--复习
文档属性
| 名称 | 28.1 锐角三角函数(4)--复习 |  | |
| 格式 | zip | ||
| 文件大小 | 131.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-31 11:39:38 | ||
图片预览





文档简介
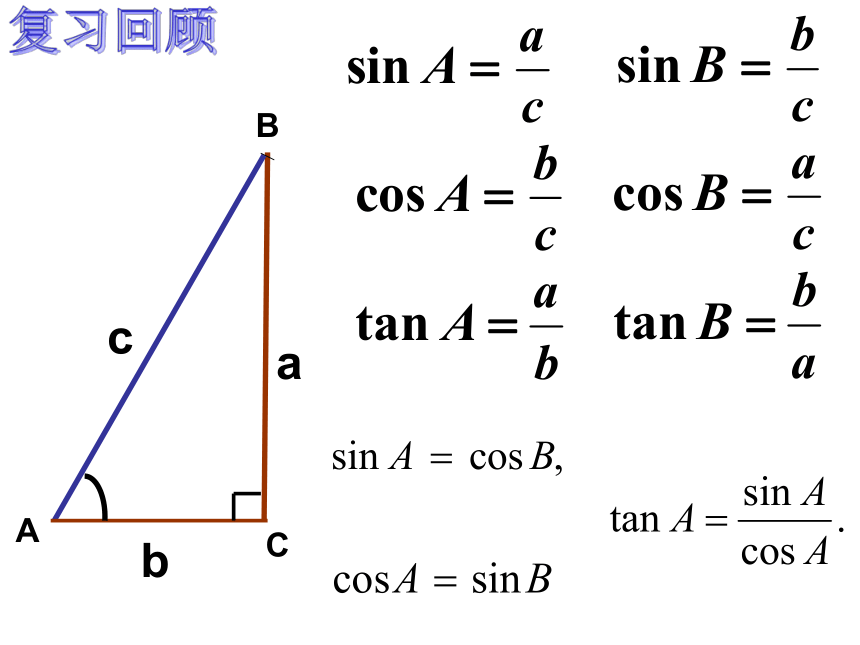
课件16张PPT。28.1 锐角三角函数(4) AB C复习回顾acb[思考] 操场上有一旗杆,老师让小明去测量它的高度。 小明站在离旗杆底部10m远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高1m,然后他很快就算出旗杆的高度了。 你知道小明是怎样算出的吗?3401米10米驶向胜利的彼岸利用计算器求下列锐角的三角函数值 (精确到0.0001)
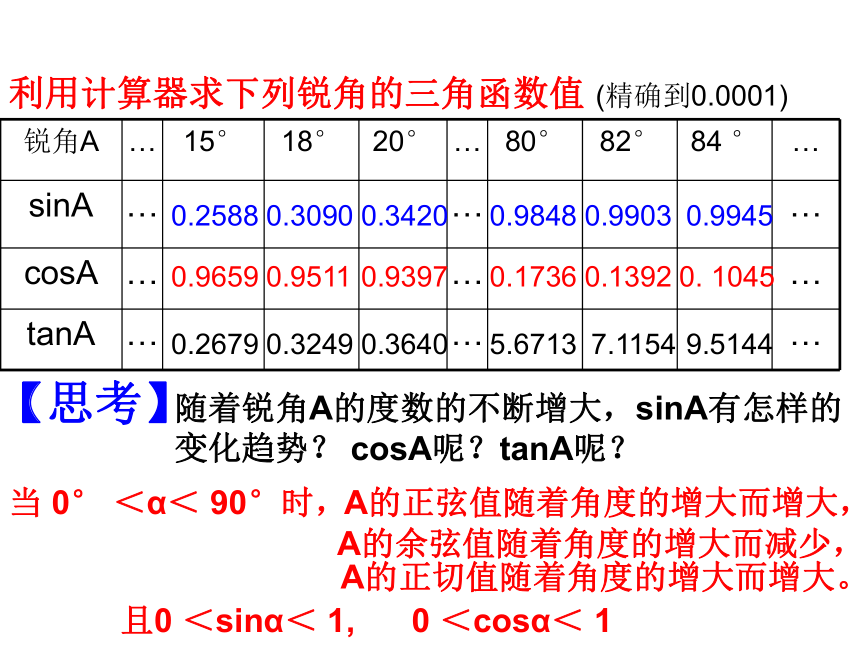
(1)sin18°(2)tan30°36′(3)cos51°42′20″驶向胜利的彼岸已知下列锐角的三角函数值, 利用计算器求相应的角度.(1)已知sinα=0.2974,求锐角α(精确到1″)(2)已知cosβ=0.4511,求锐角β(精确到1′)(3)已知tanβ=1.4036,求锐角β(精确到1°)利用计算器求下列锐角的三角函数值 (精确到0.0001)0.25880.30900.34200.98480.99030.99450.96590.95110.93970.17360.13920. 10450.26790.32490.36405.67137.11549.5144【思考】随着锐角A的度数的不断增大,sinA有怎样的变化趋势?cosA呢?tanA呢?当 0° <α< 90°时,A的正弦值随着角度的增大而增大,A的余弦值随着角度的增大而减少, A的正切值随着角度的增大而增大。且0 <sinα< 1,0 <cosα< 11 填空:比较大小><>练习:2.当∠A为锐角,且tanA=2,那么∠A 的范围是 ( )练习:A【应用新知】例 1 在Rt△ABC中, ∠C=90°,已知AC=21,AB=29,求∠A的度数。例2、一段公路弯道呈弧形,测得弯道
AB两端的距离为200米,AB 的半径为1000米,求弯道的长(精确到0.1米)⌒⌒ABOR┓D 操场上有一旗杆,老师让小明去测量它的高度。 小明站在离旗杆底部10m远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高1m,然后他很快就算出旗杆的高度了。 你知道小明是怎样算出的吗?3401米10米3.在等腰△ABC中,顶角∠ACB=108°,腰AC=10cm,求底边AB的长及△ABC的面积。练习:┓D谈谈今天的收获畅所欲言今天作业:1 作业本(1) P21---22 2 课时作业本 P80 1、利用计算器求下列各式值 (精确到0.01)
(1)sin28°-2cos35°+tan72°选自作业本(1)P21 第2题解:原式=0.42-1.64+3.08
=1.86解:原式≈0.423-1.638+3.077
=1.86作业分析2、根据下列条件,求锐角A的大小 (精确到1″)
作业分析选自作业本(1)P22 第3题(2)cosA=0.7857计算器显示:38°12′52.32″结果应该是:38°12′52″(3)tanA=1.4036计算器显示:54°31′54.8″结果应该是:54°31′55″
(1)sin18°(2)tan30°36′(3)cos51°42′20″驶向胜利的彼岸已知下列锐角的三角函数值, 利用计算器求相应的角度.(1)已知sinα=0.2974,求锐角α(精确到1″)(2)已知cosβ=0.4511,求锐角β(精确到1′)(3)已知tanβ=1.4036,求锐角β(精确到1°)利用计算器求下列锐角的三角函数值 (精确到0.0001)0.25880.30900.34200.98480.99030.99450.96590.95110.93970.17360.13920. 10450.26790.32490.36405.67137.11549.5144【思考】随着锐角A的度数的不断增大,sinA有怎样的变化趋势?cosA呢?tanA呢?当 0° <α< 90°时,A的正弦值随着角度的增大而增大,A的余弦值随着角度的增大而减少, A的正切值随着角度的增大而增大。且0 <sinα< 1,0 <cosα< 11 填空:比较大小><>练习:2.当∠A为锐角,且tanA=2,那么∠A 的范围是 ( )练习:A【应用新知】例 1 在Rt△ABC中, ∠C=90°,已知AC=21,AB=29,求∠A的度数。例2、一段公路弯道呈弧形,测得弯道
AB两端的距离为200米,AB 的半径为1000米,求弯道的长(精确到0.1米)⌒⌒ABOR┓D 操场上有一旗杆,老师让小明去测量它的高度。 小明站在离旗杆底部10m远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高1m,然后他很快就算出旗杆的高度了。 你知道小明是怎样算出的吗?3401米10米3.在等腰△ABC中,顶角∠ACB=108°,腰AC=10cm,求底边AB的长及△ABC的面积。练习:┓D谈谈今天的收获畅所欲言今天作业:1 作业本(1) P21---22 2 课时作业本 P80 1、利用计算器求下列各式值 (精确到0.01)
(1)sin28°-2cos35°+tan72°选自作业本(1)P21 第2题解:原式=0.42-1.64+3.08
=1.86解:原式≈0.423-1.638+3.077
=1.86作业分析2、根据下列条件,求锐角A的大小 (精确到1″)
作业分析选自作业本(1)P22 第3题(2)cosA=0.7857计算器显示:38°12′52.32″结果应该是:38°12′52″(3)tanA=1.4036计算器显示:54°31′54.8″结果应该是:54°31′55″
