华东师大版数学八年级下册 专题课堂(九) 矩形的折叠问题(课件)(共13张PPT)
文档属性
| 名称 | 华东师大版数学八年级下册 专题课堂(九) 矩形的折叠问题(课件)(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 379.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 23:37:28 | ||
图片预览



文档简介
(共13张PPT)
数学 八年级下册 华师版
第19章 矩形、菱形与正方形
专题课堂(九) 矩形的折叠问题
类型一 沿矩形对角线所在直线对折
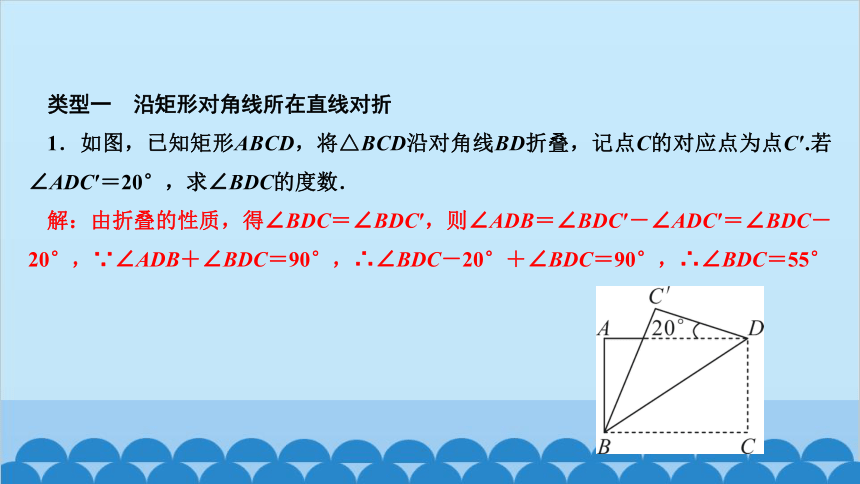
1.如图,已知矩形ABCD,将△BCD沿对角线BD折叠,记点C的对应点为点C′.若∠ADC′=20°,求∠BDC的度数.
解:由折叠的性质,得∠BDC=∠BDC′,则∠ADB=∠BDC′-∠ADC′=∠BDC-20°,∵∠ADB+∠BDC=90°,∴∠BDC-20°+∠BDC=90°,∴∠BDC=55°
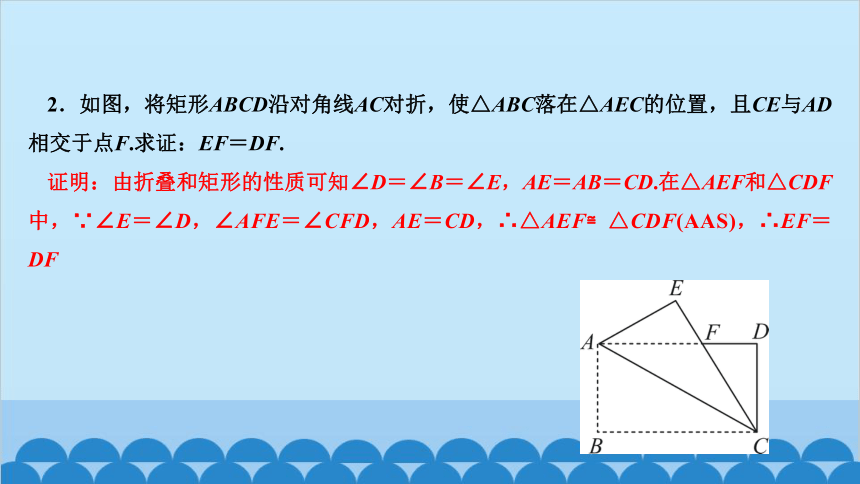
2.如图,将矩形ABCD沿对角线AC对折,使△ABC落在△AEC的位置,且CE与AD相交于点F.求证:EF=DF.
证明:由折叠和矩形的性质可知∠D=∠B=∠E,AE=AB=CD.在△AEF和△CDF中,∵∠E=∠D,∠AFE=∠CFD,AE=CD,∴△AEF≌△CDF(AAS),∴EF=DF
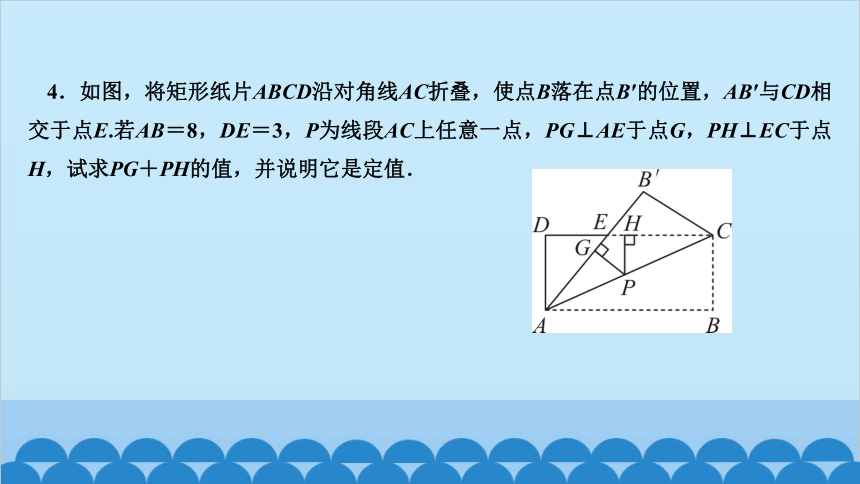
4.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落在点B′的位置,AB′与CD相交于点E.若AB=8,DE=3,P为线段AC上任意一点,PG⊥AE于点G,PH⊥EC于点H,试求PG+PH的值,并说明它是定值.
类型二 沿仅过矩形一个顶点的直线对折
5.如图,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,求AG的长.
6.如图,折叠矩形ABCD,使顶点D与BC边上的点F重合.如果AB=6,AD=10,求BF,DE的长.
7.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的点F处,已知CE=3 cm,AB=8 cm,求图中阴影部分的面积.
类型三 沿矩形对角线的垂直平分线对折
8.把一张矩形纸片ABCD按图所示方式折叠,使点B和点D重合,折痕为EF.若AB=3 cm,BC=5 cm,求重叠部分△DEF的面积.
9.如图,在矩形ABCD中,沿EF将矩形折叠,使A,C两点重合,点D落在点G处.
(1)求证:△ABE≌△AGF;
(2)若AB=6,BC=8,求△ABE的面积.
解:(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠AFE=∠FEC.又∵∠AEF=∠FEC,∴∠AFE=∠AEF,∴AE=AF.由折叠及矩形的性质,得AG=CD=AB,∠G=∠D=∠B=90°.在Rt△ABE和Rt△AGF中,∵AB=AG,AE=AF,∴Rt△ABE≌Rt△AGF(HL)
10.如图,将矩形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
解:(1)证明:∵四边形ABCD是矩形,∴AB∥CD,∴∠CFE=∠FEA.又∵∠CEF=∠FEA,∴∠CEF=∠CFE,∴EC=FC.由折叠及矩形的性质,得GC=AD=BC,∠G=∠D=∠B=90°.在Rt△FGC和Rt△EBC中,∵FC=EC,GC=BC,∴Rt△FGC≌Rt△EBC(HL)
数学 八年级下册 华师版
第19章 矩形、菱形与正方形
专题课堂(九) 矩形的折叠问题
类型一 沿矩形对角线所在直线对折
1.如图,已知矩形ABCD,将△BCD沿对角线BD折叠,记点C的对应点为点C′.若∠ADC′=20°,求∠BDC的度数.
解:由折叠的性质,得∠BDC=∠BDC′,则∠ADB=∠BDC′-∠ADC′=∠BDC-20°,∵∠ADB+∠BDC=90°,∴∠BDC-20°+∠BDC=90°,∴∠BDC=55°
2.如图,将矩形ABCD沿对角线AC对折,使△ABC落在△AEC的位置,且CE与AD相交于点F.求证:EF=DF.
证明:由折叠和矩形的性质可知∠D=∠B=∠E,AE=AB=CD.在△AEF和△CDF中,∵∠E=∠D,∠AFE=∠CFD,AE=CD,∴△AEF≌△CDF(AAS),∴EF=DF
4.如图,将矩形纸片ABCD沿对角线AC折叠,使点B落在点B′的位置,AB′与CD相交于点E.若AB=8,DE=3,P为线段AC上任意一点,PG⊥AE于点G,PH⊥EC于点H,试求PG+PH的值,并说明它是定值.
类型二 沿仅过矩形一个顶点的直线对折
5.如图,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,求AG的长.
6.如图,折叠矩形ABCD,使顶点D与BC边上的点F重合.如果AB=6,AD=10,求BF,DE的长.
7.如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的点F处,已知CE=3 cm,AB=8 cm,求图中阴影部分的面积.
类型三 沿矩形对角线的垂直平分线对折
8.把一张矩形纸片ABCD按图所示方式折叠,使点B和点D重合,折痕为EF.若AB=3 cm,BC=5 cm,求重叠部分△DEF的面积.
9.如图,在矩形ABCD中,沿EF将矩形折叠,使A,C两点重合,点D落在点G处.
(1)求证:△ABE≌△AGF;
(2)若AB=6,BC=8,求△ABE的面积.
解:(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠AFE=∠FEC.又∵∠AEF=∠FEC,∴∠AFE=∠AEF,∴AE=AF.由折叠及矩形的性质,得AG=CD=AB,∠G=∠D=∠B=90°.在Rt△ABE和Rt△AGF中,∵AB=AG,AE=AF,∴Rt△ABE≌Rt△AGF(HL)
10.如图,将矩形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
解:(1)证明:∵四边形ABCD是矩形,∴AB∥CD,∴∠CFE=∠FEA.又∵∠CEF=∠FEA,∴∠CEF=∠CFE,∴EC=FC.由折叠及矩形的性质,得GC=AD=BC,∠G=∠D=∠B=90°.在Rt△FGC和Rt△EBC中,∵FC=EC,GC=BC,∴Rt△FGC≌Rt△EBC(HL)
