28.2解直角三角形(2)
文档属性
| 名称 | 28.2解直角三角形(2) |  | |
| 格式 | zip | ||
| 文件大小 | 425.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-31 14:01:08 | ||
图片预览



文档简介
课件13张PPT。28.2 解直角三角形(2)在△ABC中,∠B=45°, ∠C=30°,AB= ,求AC和BC。在直角三角形中,除直角外,由已知两元素
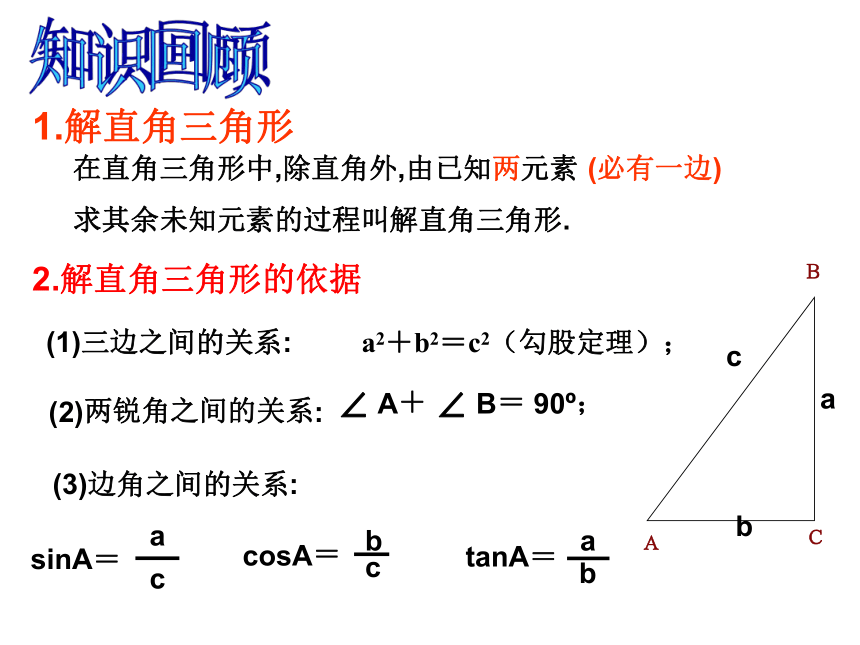
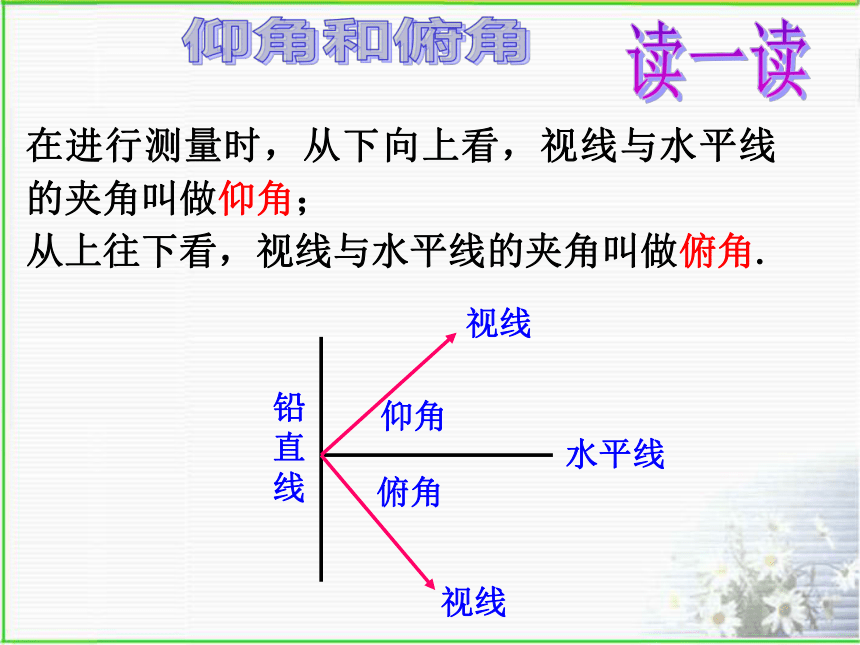
求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾(必有一边)ABCBC=5.2mAB=54.5mα高54.5m的斜塔偏离垂直中心线的距离为5.2m,求塔身偏离中心线的角度。 例 2003年10月15日“神州”5号载人航天飞船发射成功。当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行,如图,当飞船运行到地球表面上p点的正上方时,从飞船上能直接看到的地球上最远的点在什么位置?这样的最远点与P点的距离是多少(地球半径约为6400km, 取3.142,结果保留整数)?读一读在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.仰角和俯角例:热气球的探测器A显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?α=30°β=60°120ABCD1、如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°求电线杆AB的高.(精确到0.1米)亲身体验2.在山顶上D处有一铁塔,在塔顶B处测得地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,求山高CD.巩固练习1. 建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为50°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)402.两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=250,测得其底部C的俯角a=500, 求两座建筑物AB及CD的高.(精确到0.1米)感悟:利用解直角三角形的知识解决实际问题
的一般步骤:1.将实际问题抽象为数学问题;(画出平面图形,转化为解直角三角形的问题)2.根据条件的特点,适当选用锐角三角函数等
去解直角三角形;3.得到数学问题的答案;4.得到实际问题的答案.(有“弦”用“弦”; 无“弦”用“切”)1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。善于总结是学习的前提条件
求其余未知元素的过程叫解直角三角形.1.解直角三角形(1)三边之间的关系:a2+b2=c2(勾股定理);2.解直角三角形的依据(2)两锐角之间的关系:∠ A+ ∠ B= 90o;(3)边角之间的关系:sinA=知识回顾(必有一边)ABCBC=5.2mAB=54.5mα高54.5m的斜塔偏离垂直中心线的距离为5.2m,求塔身偏离中心线的角度。 例 2003年10月15日“神州”5号载人航天飞船发射成功。当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行,如图,当飞船运行到地球表面上p点的正上方时,从飞船上能直接看到的地球上最远的点在什么位置?这样的最远点与P点的距离是多少(地球半径约为6400km, 取3.142,结果保留整数)?读一读在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.仰角和俯角例:热气球的探测器A显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?α=30°β=60°120ABCD1、如图,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°求电线杆AB的高.(精确到0.1米)亲身体验2.在山顶上D处有一铁塔,在塔顶B处测得地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,求山高CD.巩固练习1. 建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为50°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)402.两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=250,测得其底部C的俯角a=500, 求两座建筑物AB及CD的高.(精确到0.1米)感悟:利用解直角三角形的知识解决实际问题
的一般步骤:1.将实际问题抽象为数学问题;(画出平面图形,转化为解直角三角形的问题)2.根据条件的特点,适当选用锐角三角函数等
去解直角三角形;3.得到数学问题的答案;4.得到实际问题的答案.(有“弦”用“弦”; 无“弦”用“切”)1、解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系。2、一些解直角三角形的问题往往与其他知识联系,所以在复习时要形成知识结构,要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。善于总结是学习的前提条件
