人教版八年级数学下册册平行四边形的性质与判定 复习课件(共15张PPT)
文档属性
| 名称 | 人教版八年级数学下册册平行四边形的性质与判定 复习课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 16:41:11 | ||
图片预览



文档简介
(共15张PPT)
复习课
利用你所学的知识画一个平行四边形ABCD,并阐述你作图的依据?
画一画
在 ABCD中, ∠A:∠B=2:7,
则∠C= 度.
2. 已知 ABCD的周长为30㎝,
AB:BC=2:3,
则AB= ㎝.
小试牛刀
40
6
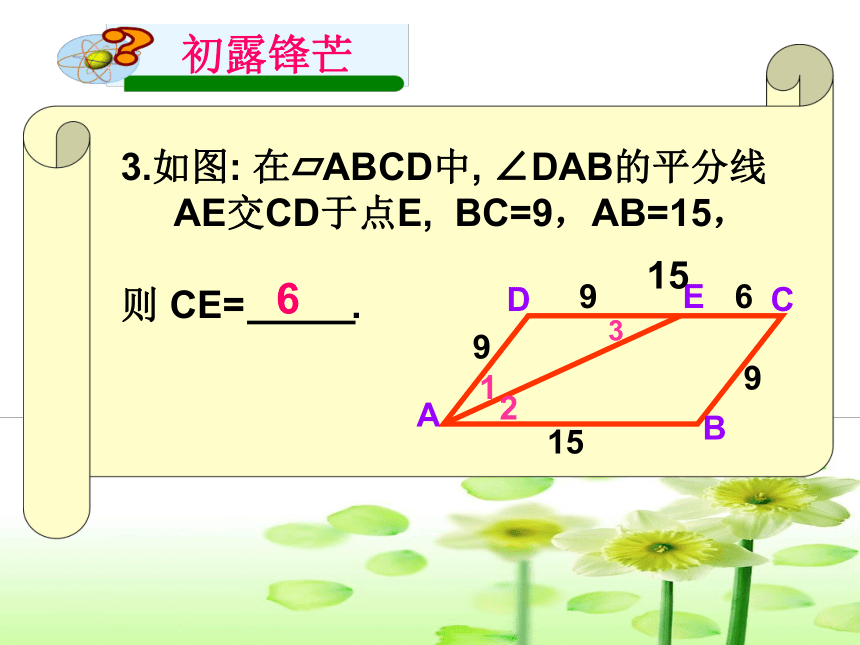
3.如图: 在 ABCD中, ∠DAB的平分线
AE交CD于点E, BC=9,AB=15,
则 CE= .
A
B
C
D
E
1
2
3
6
初露锋芒
9
15
9
15
9
6
再展雄姿
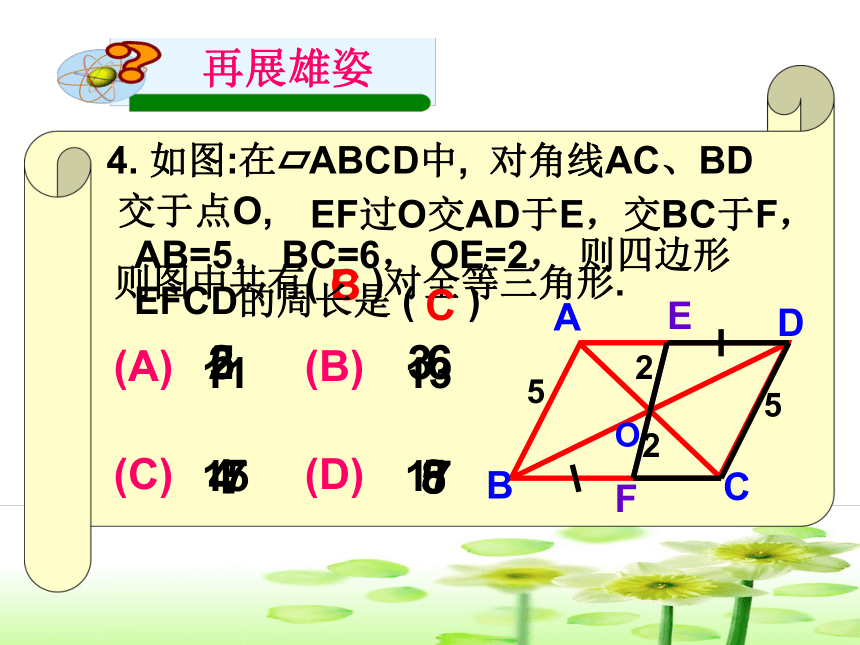
4. 如图:在 ABCD中, 对角线AC、BD
交于点O,
A
B
C
D
O
(A) (B)
(C) (D)
2 3
4 5
E
F
则图中共有( )对全等三角形.
6
7 8
C
B
EF过O交AD于E,交BC于F,
AB=5, BC=6, OE=2, 则四边形EFCD的周长是 ( )
13
15 17
C
5
5
2
2
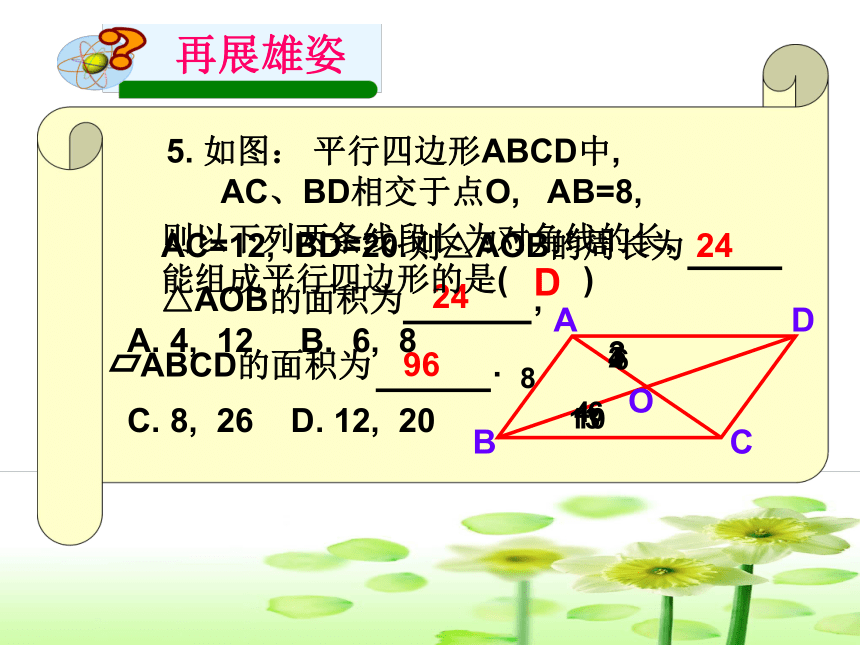
5. 如图: 平行四边形ABCD中,
AC、BD相交于点O, AB=8,
△AOB的面积为 ,
ABCD的面积为 .
A
B
C
D
O
24
24
96
8
6
10
4, 12 B. 6, 8
C. 8, 26 D. 12, 20
则以下列两条线段长为对角线的长,
能组成平行四边形的是( )
D
AC=12, BD=20.则△AOB的周长为
再展雄姿
2
6
3
4
4
13
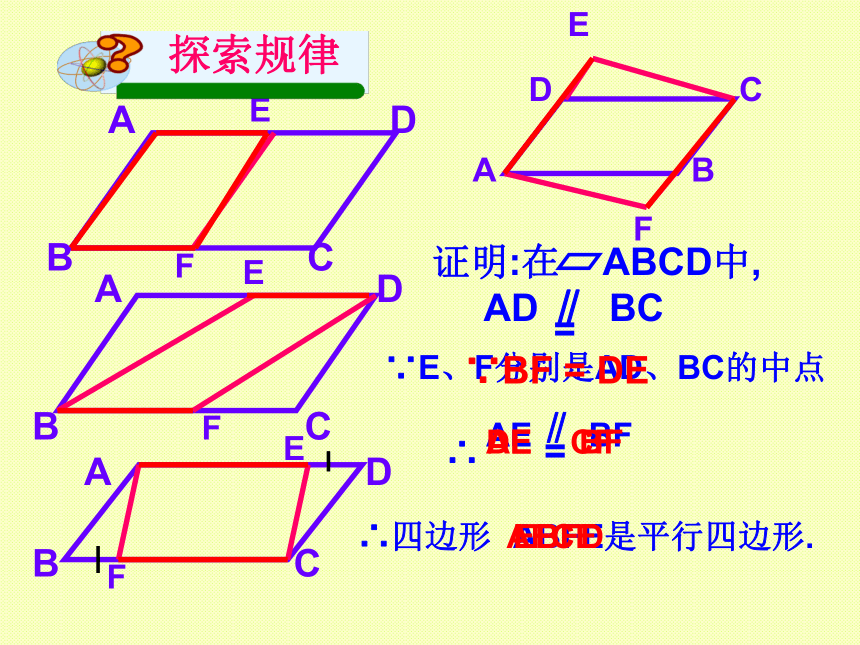
证明:在 ABCD中,
AD ∥ BC
=
∴ =
A D
B C
E
F
A D
B C
E
F
E
F
D C
A B
E
F
AE BF
DE BF
ABFE
EBFD
AE CF
AFCE
∵E、F分别是AD、BC的中点
∥
∵BF = DE
∴四边形 是平行四边形.
A D
B C
探索规律
证明: 在 ABCD中,
AB∥CD
∴∠1 = ∠2
又∵AE = CF
∴△ABE≌△CDF(SAS)
∴BE = DF
同理 DE = BF
∠3=∠4
∴∠5=∠6
∴BE∥DF
∴四边形 是平行四边形.
1
2
3
4
5
6
A
B
C
D
E
F
F
G
H
O
O
O
E
F
G
H
E
F
=
O
证明: 在 ABCD中,
OA = OC, OB = OD
∵ AE = CF
∴OA AE=OC CF
即 OE = OF
-
-
+
+
BG = DH
OB BG=OD DH
OG = OH
+
+
-
-
A D
B C
A D
B C
A D
B C
E
BEDF
EGFH
探索规律
E
F
B
A
D
C
G
H
O
如图: 在 ABCD中, AC、BD交于点O, 延长AC至F, 反向延长AC至E, 使AE=CF, 过点O画GH交AD于G, 交BC于H, 连结EH、HF、FG、GE,
求证: 四边形EHFG是平行四边形.
证明: 在 ABCD中
AD∥BC, OA=OC,
∴∠1=∠2, ∠3=∠4,
∴△AOG≌△COH
∴ OG = OH
又∵ AE=CF
∴ OE=OF
∴四边形EHFG是平行四边形.
1
2
3
4
综合应用
如图; 在 ABCD中, 以AD、BC为边作
正三角形ADE, 正三角形BCF, 连结BE,DF,
求证: 四边形EBFD是平行四边形.
A
B
C
D
E
F
1
2
3
4
证明: 在 ABCD中,
AD = BC, AB = CD,∠1 = ∠2
∵△ADE与△BCF都是正三角形,
∴AE=DE=AD, BE=CF=BC,
∠3=∠4=60°.
∴DE=BF, AE=CF,
∠1+∠3=∠2+∠4,
即 ∠EAB=∠DCF,
∴△ABE≌△DCF
∴BE=DF
∴四边形EBFD是平行四边形.
合作探究
在四边形ABCD中,若分别给出四个条件: ①AB∥CD ② AD∥ BC ③ AB=CD ④ AD=BC. 现在,以其中的两个为一组,能识别四边形ABCD为平行四边形的条件是 (只填序号,一种即可)
A
B
C
D
O
想一想
3. 如图: 在 ABCD中,∠BAD = 2∠B, ∠BCD的平分线交BA的延长线于点E,
则△EBC是 三角形.
A
B
C
E
F
D
120°
60°
60°
60°
正
初露锋芒
5.如图: 在△ABC中, AB = AC = 8,
点D 在BC上, DE∥AC交AB于点E, DF∥AB交AC于F,
则DE+DF = .
A
B
C
D
E
F
1
8
初露锋芒
通过这节课的学习,
你有哪些收获?
能与大家一起分享吗?
丰 收 园
复习课
利用你所学的知识画一个平行四边形ABCD,并阐述你作图的依据?
画一画
在 ABCD中, ∠A:∠B=2:7,
则∠C= 度.
2. 已知 ABCD的周长为30㎝,
AB:BC=2:3,
则AB= ㎝.
小试牛刀
40
6
3.如图: 在 ABCD中, ∠DAB的平分线
AE交CD于点E, BC=9,AB=15,
则 CE= .
A
B
C
D
E
1
2
3
6
初露锋芒
9
15
9
15
9
6
再展雄姿
4. 如图:在 ABCD中, 对角线AC、BD
交于点O,
A
B
C
D
O
(A) (B)
(C) (D)
2 3
4 5
E
F
则图中共有( )对全等三角形.
6
7 8
C
B
EF过O交AD于E,交BC于F,
AB=5, BC=6, OE=2, 则四边形EFCD的周长是 ( )
13
15 17
C
5
5
2
2
5. 如图: 平行四边形ABCD中,
AC、BD相交于点O, AB=8,
△AOB的面积为 ,
ABCD的面积为 .
A
B
C
D
O
24
24
96
8
6
10
4, 12 B. 6, 8
C. 8, 26 D. 12, 20
则以下列两条线段长为对角线的长,
能组成平行四边形的是( )
D
AC=12, BD=20.则△AOB的周长为
再展雄姿
2
6
3
4
4
13
证明:在 ABCD中,
AD ∥ BC
=
∴ =
A D
B C
E
F
A D
B C
E
F
E
F
D C
A B
E
F
AE BF
DE BF
ABFE
EBFD
AE CF
AFCE
∵E、F分别是AD、BC的中点
∥
∵BF = DE
∴四边形 是平行四边形.
A D
B C
探索规律
证明: 在 ABCD中,
AB∥CD
∴∠1 = ∠2
又∵AE = CF
∴△ABE≌△CDF(SAS)
∴BE = DF
同理 DE = BF
∠3=∠4
∴∠5=∠6
∴BE∥DF
∴四边形 是平行四边形.
1
2
3
4
5
6
A
B
C
D
E
F
F
G
H
O
O
O
E
F
G
H
E
F
=
O
证明: 在 ABCD中,
OA = OC, OB = OD
∵ AE = CF
∴OA AE=OC CF
即 OE = OF
-
-
+
+
BG = DH
OB BG=OD DH
OG = OH
+
+
-
-
A D
B C
A D
B C
A D
B C
E
BEDF
EGFH
探索规律
E
F
B
A
D
C
G
H
O
如图: 在 ABCD中, AC、BD交于点O, 延长AC至F, 反向延长AC至E, 使AE=CF, 过点O画GH交AD于G, 交BC于H, 连结EH、HF、FG、GE,
求证: 四边形EHFG是平行四边形.
证明: 在 ABCD中
AD∥BC, OA=OC,
∴∠1=∠2, ∠3=∠4,
∴△AOG≌△COH
∴ OG = OH
又∵ AE=CF
∴ OE=OF
∴四边形EHFG是平行四边形.
1
2
3
4
综合应用
如图; 在 ABCD中, 以AD、BC为边作
正三角形ADE, 正三角形BCF, 连结BE,DF,
求证: 四边形EBFD是平行四边形.
A
B
C
D
E
F
1
2
3
4
证明: 在 ABCD中,
AD = BC, AB = CD,∠1 = ∠2
∵△ADE与△BCF都是正三角形,
∴AE=DE=AD, BE=CF=BC,
∠3=∠4=60°.
∴DE=BF, AE=CF,
∠1+∠3=∠2+∠4,
即 ∠EAB=∠DCF,
∴△ABE≌△DCF
∴BE=DF
∴四边形EBFD是平行四边形.
合作探究
在四边形ABCD中,若分别给出四个条件: ①AB∥CD ② AD∥ BC ③ AB=CD ④ AD=BC. 现在,以其中的两个为一组,能识别四边形ABCD为平行四边形的条件是 (只填序号,一种即可)
A
B
C
D
O
想一想
3. 如图: 在 ABCD中,∠BAD = 2∠B, ∠BCD的平分线交BA的延长线于点E,
则△EBC是 三角形.
A
B
C
E
F
D
120°
60°
60°
60°
正
初露锋芒
5.如图: 在△ABC中, AB = AC = 8,
点D 在BC上, DE∥AC交AB于点E, DF∥AB交AC于F,
则DE+DF = .
A
B
C
D
E
F
1
8
初露锋芒
通过这节课的学习,
你有哪些收获?
能与大家一起分享吗?
丰 收 园
