人教版八年级数学下册册19.2.2 一次函数第3课时 课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册册19.2.2 一次函数第3课时 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 16:51:27 | ||
图片预览





文档简介
(共18张PPT)
第十九章 一次函数
19.2.2 一次函数
第3课时
1.画出函数y= x与y=3x-1的图象.
2.你在画这两个函数图象时,分别描了几个点?你为何选取这几个点?可以有不同取法吗?
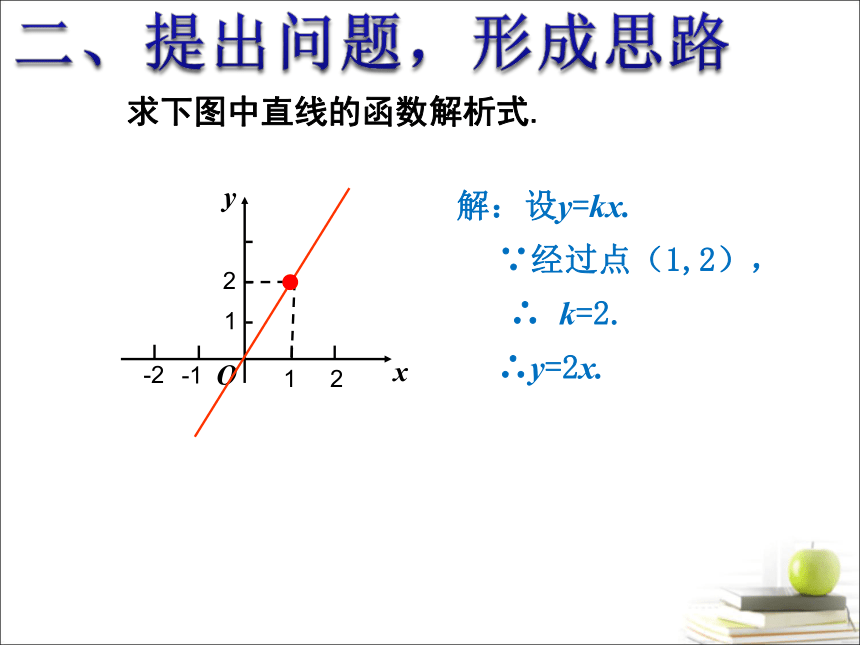
求下图中直线的函数解析式.
O
2
x
1
2
-2
-1
1
解:设y=kx.
∵经过点(1,2),
∴ k=2.
∴y=2x.
y
求下图中直线的函数解析式.
O
1
x
y
1
2
3
3
2
解:设y=kx+b.
∵经过点(2,0), (0,2),
2k+b=0,
∴y=-x+2.
b=2.
解得
k=-1,
b=2.
∴
反思小结:
确定正比例函数的解析式需要一个条件,确定一次函数的解析式需要两个条件.
例 已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
不画图,你能说出一次函数y=3x-4的图象是什么形状吗?
解:设y=kx+b.
经过点(3,5)、(-4,-9),
3k+b=5,
∴y=2x-1
解得
k=2,
b=-1.
-4k+b=-9.
像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
在前面的学习过程中我们发现数与形之间是怎样结合互化的?
函数解析式y=kx+b
一次函数的图象直线l
满足条件的两定点(x1,y1)(x2,y2)
解出
选取
选取
解出
1.写出两个一次函数,使它们的图象都经过点(-2,3).
2.生物学家研究表明,某种蛇的长度y(cm)是其尾长x(cm)的一次函数,当蛇的尾长为6 cm时,蛇长为45.5 cm;当尾长为14 cm时,蛇长为105.5 cm.当蛇的尾长为10 cm时,这条蛇的长度是多少?
y=7.5x+0.5
75.5 cm
3.一个函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,3a)与点(a,6),求这个函数的解析式.
4.小明将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经过几个月才能存够200元?
O
40
x
y
1
2
3
120
80
4
y=20x+40
8个月
5.如图,直线l是某正比例函数的图象,点A(0,12),B(3,-9)是否在该函数的图象上?
解:设 ,根据图象,得
当x = 0时,y = 0,所以点A(0,12)不在该函数的图象上;当x = 3时,y = -9 ,所以点B(3,-9)在该函数的图象上.
6.若一次函数 的图象经过点A′(-1,1),A(1,5),B(-10,-17),C(10,17)是否在该函数的图象上?
解:根据题意,得
所以 ;
当x = 1时,y = 5,所以点A(1,5)在该函数的图象上;当x = -10时,y = -17 ,所以点B(-10,-17)在该函数的图象上;当x = 10时,y = 23 ,所以点C(10,17)不在该函数的图象上.
7.如图直线l是一次函数 的图象,填空:
(1)当x = 30时,y = ________;
(2)当y = 30时,x = ________.
-18
-42
1.用待定系数法求函数解析式的一般步骤.
2.数形结合解决问题的一般思路.
1.必做题:
教材第95页练习第1题,第99页习题19.2第6、7题.
2.备选题:
(1)若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过( )
A.A(-1,1) B.B(2,2)
C.C(-2,2) D.D(2,-2)
(2)老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质:
甲:函数的图象经过第一象限;
乙:函数的图象经过第二象限;
丙:在每个象限内,y随x的增大而减小.
请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数解析式: .
C
(3)如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
①求出h与d之间的函数解析式(不要求写出自变量d的取值范围).
②某人身高为196 cm,一般情况下他的指距应是多少?
解:(1)设h与d之间的函数关系式为:
h=kd+b. 把d=20,h=160,d=21,h=169,
分别代入得,
20k+b=160,
21k+b=169. 解得k=9,b=-20,
即h=9d-20. (2)当h=196时,196=9d-20,解得d=24(cm).
第十九章 一次函数
19.2.2 一次函数
第3课时
1.画出函数y= x与y=3x-1的图象.
2.你在画这两个函数图象时,分别描了几个点?你为何选取这几个点?可以有不同取法吗?
求下图中直线的函数解析式.
O
2
x
1
2
-2
-1
1
解:设y=kx.
∵经过点(1,2),
∴ k=2.
∴y=2x.
y
求下图中直线的函数解析式.
O
1
x
y
1
2
3
3
2
解:设y=kx+b.
∵经过点(2,0), (0,2),
2k+b=0,
∴y=-x+2.
b=2.
解得
k=-1,
b=2.
∴
反思小结:
确定正比例函数的解析式需要一个条件,确定一次函数的解析式需要两个条件.
例 已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
不画图,你能说出一次函数y=3x-4的图象是什么形状吗?
解:设y=kx+b.
经过点(3,5)、(-4,-9),
3k+b=5,
∴y=2x-1
解得
k=2,
b=-1.
-4k+b=-9.
像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
在前面的学习过程中我们发现数与形之间是怎样结合互化的?
函数解析式y=kx+b
一次函数的图象直线l
满足条件的两定点(x1,y1)(x2,y2)
解出
选取
选取
解出
1.写出两个一次函数,使它们的图象都经过点(-2,3).
2.生物学家研究表明,某种蛇的长度y(cm)是其尾长x(cm)的一次函数,当蛇的尾长为6 cm时,蛇长为45.5 cm;当尾长为14 cm时,蛇长为105.5 cm.当蛇的尾长为10 cm时,这条蛇的长度是多少?
y=7.5x+0.5
75.5 cm
3.一个函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,3a)与点(a,6),求这个函数的解析式.
4.小明将父母给的零用钱按每月相等的数额存放在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经过几个月才能存够200元?
O
40
x
y
1
2
3
120
80
4
y=20x+40
8个月
5.如图,直线l是某正比例函数的图象,点A(0,12),B(3,-9)是否在该函数的图象上?
解:设 ,根据图象,得
当x = 0时,y = 0,所以点A(0,12)不在该函数的图象上;当x = 3时,y = -9 ,所以点B(3,-9)在该函数的图象上.
6.若一次函数 的图象经过点A′(-1,1),A(1,5),B(-10,-17),C(10,17)是否在该函数的图象上?
解:根据题意,得
所以 ;
当x = 1时,y = 5,所以点A(1,5)在该函数的图象上;当x = -10时,y = -17 ,所以点B(-10,-17)在该函数的图象上;当x = 10时,y = 23 ,所以点C(10,17)不在该函数的图象上.
7.如图直线l是一次函数 的图象,填空:
(1)当x = 30时,y = ________;
(2)当y = 30时,x = ________.
-18
-42
1.用待定系数法求函数解析式的一般步骤.
2.数形结合解决问题的一般思路.
1.必做题:
教材第95页练习第1题,第99页习题19.2第6、7题.
2.备选题:
(1)若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过( )
A.A(-1,1) B.B(2,2)
C.C(-2,2) D.D(2,-2)
(2)老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质:
甲:函数的图象经过第一象限;
乙:函数的图象经过第二象限;
丙:在每个象限内,y随x的增大而减小.
请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数解析式: .
C
(3)如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
①求出h与d之间的函数解析式(不要求写出自变量d的取值范围).
②某人身高为196 cm,一般情况下他的指距应是多少?
解:(1)设h与d之间的函数关系式为:
h=kd+b. 把d=20,h=160,d=21,h=169,
分别代入得,
20k+b=160,
21k+b=169. 解得k=9,b=-20,
即h=9d-20. (2)当h=196时,196=9d-20,解得d=24(cm).
