人教版八年级数学下册册 18.1.2 平行四边形的判定 课件 (共20张PPT)
文档属性
| 名称 | 人教版八年级数学下册册 18.1.2 平行四边形的判定 课件 (共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 16:55:07 | ||
图片预览




文档简介
(共20张PPT)
第18章平行四边形
18.1.2 平行四边形的判定(一)
平行四边形性质是什么?请按边、角、对角线的顺序回答
它们的逆命题怎样叙述?
请用“两边分别平行的四边形是平行四边形” 完成下面命题的证明.
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
A
B
C
D
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
D
B
A
C
2
1
3
4
AB=CD(已知)
AD=CB (已知)
AC=CA (公共边)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
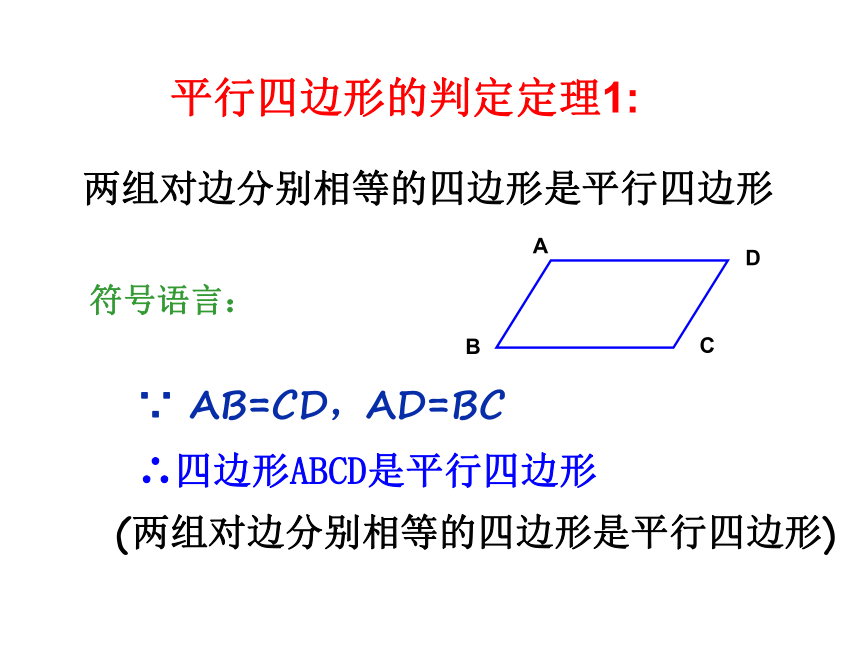
两组对边分别相等的四边形是平行四边形
平行四边形的判定定理1:
符号语言:
A
B
C
D
∵ AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
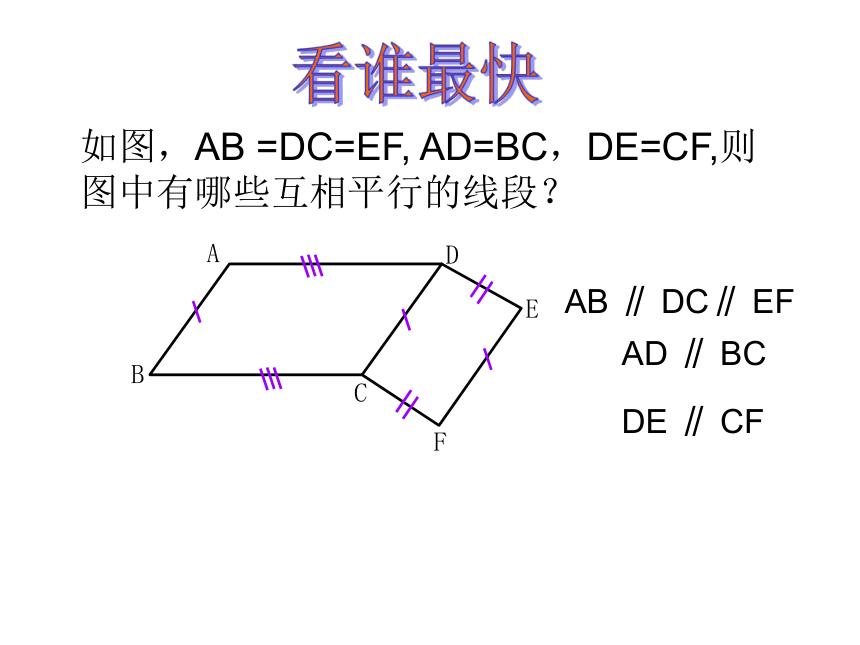
如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
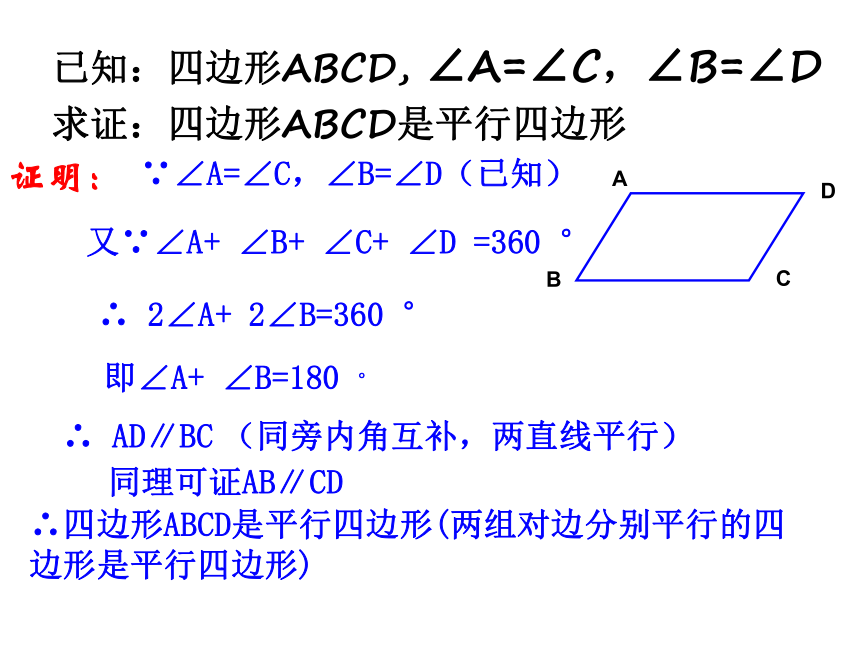
已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
A
B
C
D
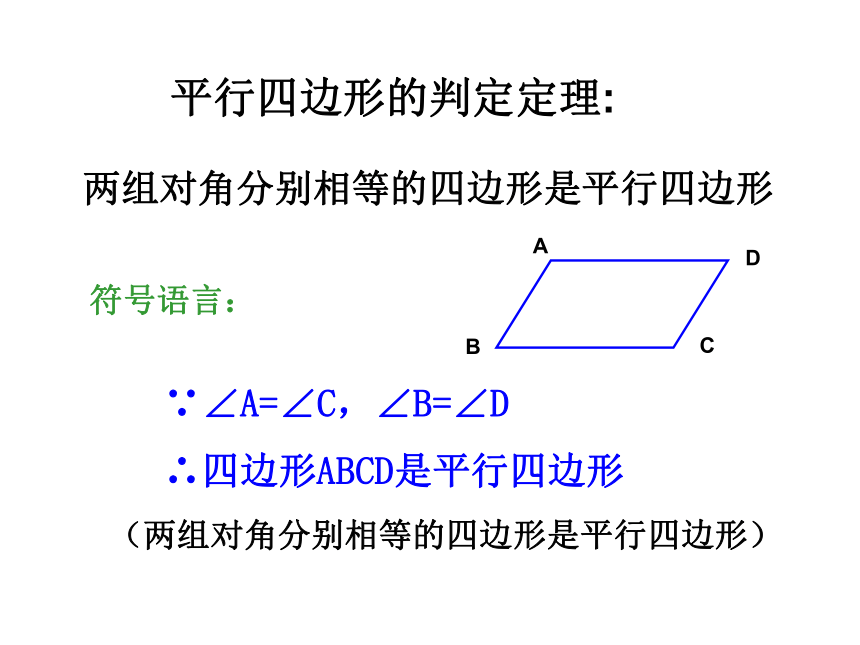
两组对角分别相等的四边形是平行四边形
平行四边形的判定定理:
符号语言:
A
B
C
D
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形)
O
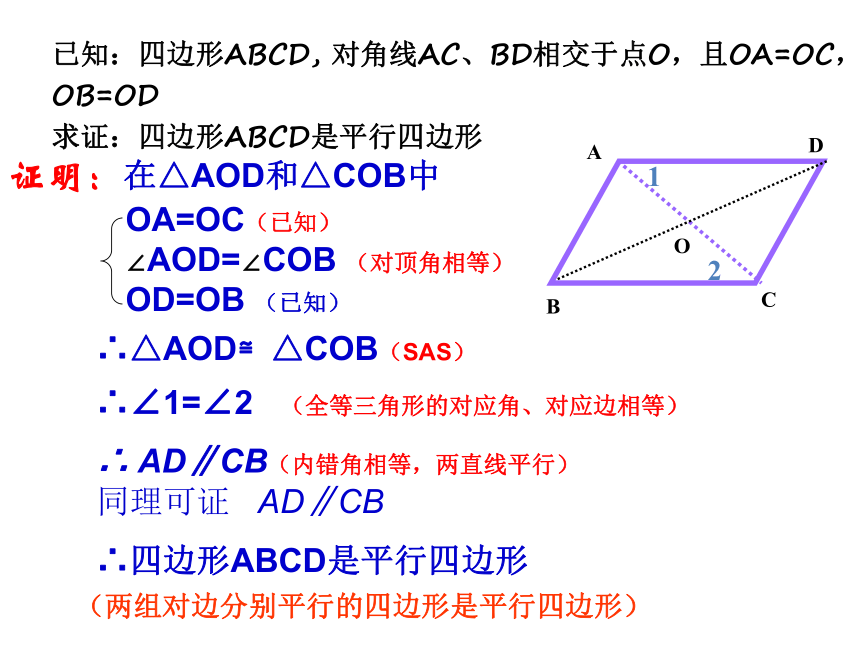
已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:
在△AOD和△COB中
OA=OC(已知)
∠AOD=∠COB (对顶角相等)
OD=OB (已知)
∴△AOD≌△COB(SAS)
∴∠1=∠2 (全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)同理可证 AD∥CB
∴四边形ABCD是平行四边形
B
A
C
2
1
D
(两组对边分别平行的四边形是平行四边形)
对角线互相平分的四边形是平行四边形
平行四边形的判定定理3:
符号语言:
A
B
C
D
O
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
交流展示 下列四边形哪些是平行四边形 请说明理由?
A
D
C
B
110°
70°
110°
(1)
(3)
(2)
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
例3 如图:平行四边形ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF,求证: 四边形BFDE是平行四边形。
C
B
O
D
A
F
E
你还有其他的证明方法吗?
证明:
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
合作探究
已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
变式1
A
B
C
D
E
F
变式2
O
如图:平行四边形ABCD的对角线AC、BD相交
于点O,点E,F 分别在AC 两侧的延长线上,并
且AE=CF. 求证: 四边形BFDE是平行四边形。
已知:E、F是平行四边形ABCD对角线AC上的两点,并且BE ∥ DF.
求证:四边形BFDE是平行四边形
D
A
B
C
E
F
变式3
巩固练习
1、如图(1),在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC=___ cm,CD=___ cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=__ _cm,DO=__ _cm时,四边形ABCD为平行四边形.
2、下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形 的是( )
A.1:2:3:4 B.2:2:3:3
C.2:3:2:3 D.2:3:3:2
3、下列条件中能判断四边形是平行四边形的是 ( ).
(A)对角线互相垂直 (B)对角线相等
(C)对角线互相垂直且相等 (D)对角线互相平分
8
4
4
5
C
D
3、如图,口ABCD的对角线AC、BD相交于点O,E、F分别是OA,OC的中点.求证:BE=DF.
A
B
C
D
E
F
O
证明:∵四边形ABCD是平行四边形
∴OA=OC AB=CD
AB∥CD
∴∠EAB=∠FCD
∵点E、F分别是OA、OC的中点
∴AE=CF
∴△ABE≌△CDF
∴BE=DF
4、 已知:如图,在平行四边形ABCD中,E,F分别是AB,DC上的两点,且AE=CF.求证:BD,EF互相平分
反思小结:
1.本节课你学会了几种平行四边形的判定方法
2.本节课解决问题的思想方法:
(2)碰到平行四边形的问题常转化为三角形来解决。
(1)解决一个数学问题,常要通过“动手实践”----“ 猜想”----“验证猜想(证明)”-----“得出结论”
第18章平行四边形
18.1.2 平行四边形的判定(一)
平行四边形性质是什么?请按边、角、对角线的顺序回答
它们的逆命题怎样叙述?
请用“两边分别平行的四边形是平行四边形” 完成下面命题的证明.
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
A
B
C
D
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
D
B
A
C
2
1
3
4
AB=CD(已知)
AD=CB (已知)
AC=CA (公共边)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形
平行四边形的判定定理1:
符号语言:
A
B
C
D
∵ AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
A
B
C
D
两组对角分别相等的四边形是平行四边形
平行四边形的判定定理:
符号语言:
A
B
C
D
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
(两组对角分别相等的四边形是平行四边形)
O
已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:
在△AOD和△COB中
OA=OC(已知)
∠AOD=∠COB (对顶角相等)
OD=OB (已知)
∴△AOD≌△COB(SAS)
∴∠1=∠2 (全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)同理可证 AD∥CB
∴四边形ABCD是平行四边形
B
A
C
2
1
D
(两组对边分别平行的四边形是平行四边形)
对角线互相平分的四边形是平行四边形
平行四边形的判定定理3:
符号语言:
A
B
C
D
O
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
交流展示 下列四边形哪些是平行四边形 请说明理由?
A
D
C
B
110°
70°
110°
(1)
(3)
(2)
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
例3 如图:平行四边形ABCD的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF,求证: 四边形BFDE是平行四边形。
C
B
O
D
A
F
E
你还有其他的证明方法吗?
证明:
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即 EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
合作探究
已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
变式1
A
B
C
D
E
F
变式2
O
如图:平行四边形ABCD的对角线AC、BD相交
于点O,点E,F 分别在AC 两侧的延长线上,并
且AE=CF. 求证: 四边形BFDE是平行四边形。
已知:E、F是平行四边形ABCD对角线AC上的两点,并且BE ∥ DF.
求证:四边形BFDE是平行四边形
D
A
B
C
E
F
变式3
巩固练习
1、如图(1),在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么当BC=___ cm,CD=___ cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,那么当AO=__ _cm,DO=__ _cm时,四边形ABCD为平行四边形.
2、下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形 的是( )
A.1:2:3:4 B.2:2:3:3
C.2:3:2:3 D.2:3:3:2
3、下列条件中能判断四边形是平行四边形的是 ( ).
(A)对角线互相垂直 (B)对角线相等
(C)对角线互相垂直且相等 (D)对角线互相平分
8
4
4
5
C
D
3、如图,口ABCD的对角线AC、BD相交于点O,E、F分别是OA,OC的中点.求证:BE=DF.
A
B
C
D
E
F
O
证明:∵四边形ABCD是平行四边形
∴OA=OC AB=CD
AB∥CD
∴∠EAB=∠FCD
∵点E、F分别是OA、OC的中点
∴AE=CF
∴△ABE≌△CDF
∴BE=DF
4、 已知:如图,在平行四边形ABCD中,E,F分别是AB,DC上的两点,且AE=CF.求证:BD,EF互相平分
反思小结:
1.本节课你学会了几种平行四边形的判定方法
2.本节课解决问题的思想方法:
(2)碰到平行四边形的问题常转化为三角形来解决。
(1)解决一个数学问题,常要通过“动手实践”----“ 猜想”----“验证猜想(证明)”-----“得出结论”
