人教版八年级数学下册册 18.2.1.2矩形判定 课件(共19张PPT)
文档属性
| 名称 | 人教版八年级数学下册册 18.2.1.2矩形判定 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 16:56:22 | ||
图片预览





文档简介
(共19张PPT)
八年级 下册
18.2.1 矩形的判定
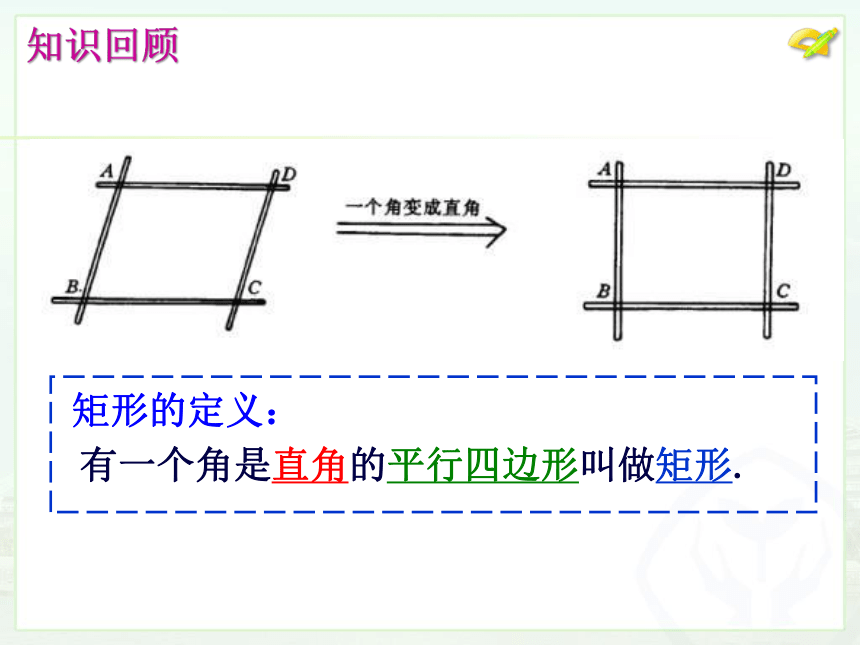
知识回顾
矩形的定义:
有一个角是直角的平行四边形叫做矩形.
边
角
对角线
周长
面积
对称性
对角线互相平分且相等
四个角都是直角
对边平行且相等
邻边之和 X 2
长 X 宽
轴对称,中心对称
矩形性质及特点
知识回顾
一天,小丽和吴娟到一个商店准备给今天要过生日的肖华买生日礼物,选了半天,她们俩最后决定买相框送给她,在里面摆放她们三个好朋友的相片,为了保证相框摆放的美观性,她们选择了矩形的相框,那么她们是用什么方法可以知道她们拿的就是矩形相框呢
思考与探究
除了矩形的定义外,有没有其他判定矩形的方法呢?
类比探究
提示:你还记得学习平行四边形的判定时,
我们是如何猜想并进行证明的吗?
平行四边形 性质 判定
边
角
对角线
对边平行且相等
对角相等,邻角互补
互相平分
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
4.两组对角分别相等的四边形是平行四边形
5.两条对角线互相平分的四边形是平行四边形
证明
逆命题
(修正)
性质
猜想
判定定理
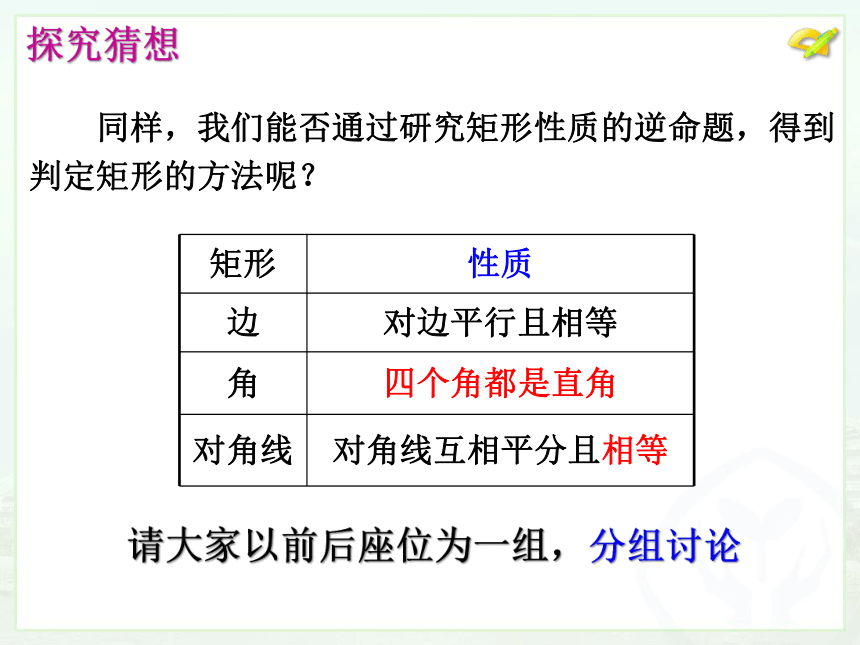
同样,我们能否通过研究矩形性质的逆命题,得到
判定矩形的方法呢?
探究猜想
矩形 性质
边 对边平行且相等
角 四个角都是直角
对角线 对角线互相平分且相等
请大家以前后座位为一组,分组讨论
猜想展示
你的小组有哪些猜想?
如何证明?
这些猜想都是真命题吗?
矩形 性质
边 对边平行且相等
角 四个角都是直角
对角线 对角线互相平分且相等
证明猜想
◆有三个角是直角的四边形是矩形吗
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
证明:
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
D
B
C
A
∴四边形ABCD是矩形.
证明猜想
证明:
在
ABCD中
AB=DC,BD=CA,AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD +∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形
(有一个内角是直角的平行四边形是矩形)
◆对角线相等的平行四边形是矩形吗?
四边形ABCD是平行四边形,AC=BD
四边形ABCD是矩形
已知:
求证:
推论:对角线互相平分且相等的四边形是矩形
证明猜想
四边形ABCD
是矩形
整理归纳
方法1:有一个角是直角的平行四边形叫做矩形
方法2:对角线相等的平行四边形是矩形
方法3:有三个角是直角的四边形是矩形
方法4:对角线相等且互相平分的四边形是矩形
你能归纳矩形的判定方法吗?
四边形
平行
四边形
一个角
是直角
矩形
对角线
相等
矩形
三个角
是直角
矩形
矩形
对角线互相
平分且相等
整理归纳
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则相框符合规格
测量出三个内角的度数,如果三个内角都是直角,则相框符合规格
分别测量出相框四边和两条对角线的长度,如果相框两组对边长度、两条对角线的长度分别相等,那么相框符合规格
方案:
方案:
方案:
实际应用
小丽和吴娟是怎样知道所买的相框是矩形的呢
判断
1.对角线相等的四边形是矩形。 ( )
2.对角线互相平分且相等的四边形是矩形。 ( )
3.有一个角是直角的四边形是矩形。 ( )
4.四个角都是直角的四边形是矩形。 ( )
5.四个角都相等的四边形是矩形。 ( )
6.对角线相等且有一个角是直角的四边形是矩形。 ( )
7.对角线相等且互相垂直的四边形是矩形。 ( )
8.两组对边分别平行,且对角线相等的四边形是矩形. ( )
辨一辨
例1 已知:如图,矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,
求证:四边形EFGH是矩形
证明:
∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵ E、F、G、H分别是AO、BO、CO、DO的中点
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角线互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形)。
例2:已知:如图,平行四边形ABCD的四个内角的平分线 ,分别相交于点E,F,G,H.
求证:四边形EFGH是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC
∴∠DAB+∠ABC=180°
又∵AE平分∠DAB,BG平分∠ABC
∴∠AFB=1800—(∠EAB+∠ABG)=90°
同理:∠AED=∠BGC=∠CHD=90°
四边形EFGH是矩形
∴∠EAB+∠ABG= ×180°=90°
∴∠EAB= ∠DAB, ∠ABG = ∠ABC
∴∠AED=∠BGC=∠ GFE =∠GHE=90°
课堂小结
今天这堂课你有什么收获?
四边形
平行
四边形
一个角
是直角
矩形
对角线
相等
矩形
三个角
是直角
矩形
矩形
对角线互相
平分且相等
1、渗透了类比的学习方法
2、体会了图形判定探究的一般思路
证明
逆命题
(修正)
性质
猜想
判定定理
1、教材习题18.2中第1、2、3题。
2、完成《基础训练》对应课时的习题。
课后作业
八年级 下册
18.2.1 矩形的判定
知识回顾
矩形的定义:
有一个角是直角的平行四边形叫做矩形.
边
角
对角线
周长
面积
对称性
对角线互相平分且相等
四个角都是直角
对边平行且相等
邻边之和 X 2
长 X 宽
轴对称,中心对称
矩形性质及特点
知识回顾
一天,小丽和吴娟到一个商店准备给今天要过生日的肖华买生日礼物,选了半天,她们俩最后决定买相框送给她,在里面摆放她们三个好朋友的相片,为了保证相框摆放的美观性,她们选择了矩形的相框,那么她们是用什么方法可以知道她们拿的就是矩形相框呢
思考与探究
除了矩形的定义外,有没有其他判定矩形的方法呢?
类比探究
提示:你还记得学习平行四边形的判定时,
我们是如何猜想并进行证明的吗?
平行四边形 性质 判定
边
角
对角线
对边平行且相等
对角相等,邻角互补
互相平分
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
4.两组对角分别相等的四边形是平行四边形
5.两条对角线互相平分的四边形是平行四边形
证明
逆命题
(修正)
性质
猜想
判定定理
同样,我们能否通过研究矩形性质的逆命题,得到
判定矩形的方法呢?
探究猜想
矩形 性质
边 对边平行且相等
角 四个角都是直角
对角线 对角线互相平分且相等
请大家以前后座位为一组,分组讨论
猜想展示
你的小组有哪些猜想?
如何证明?
这些猜想都是真命题吗?
矩形 性质
边 对边平行且相等
角 四个角都是直角
对角线 对角线互相平分且相等
证明猜想
◆有三个角是直角的四边形是矩形吗
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
证明:
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
D
B
C
A
∴四边形ABCD是矩形.
证明猜想
证明:
在
ABCD中
AB=DC,BD=CA,AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD +∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形
(有一个内角是直角的平行四边形是矩形)
◆对角线相等的平行四边形是矩形吗?
四边形ABCD是平行四边形,AC=BD
四边形ABCD是矩形
已知:
求证:
推论:对角线互相平分且相等的四边形是矩形
证明猜想
四边形ABCD
是矩形
整理归纳
方法1:有一个角是直角的平行四边形叫做矩形
方法2:对角线相等的平行四边形是矩形
方法3:有三个角是直角的四边形是矩形
方法4:对角线相等且互相平分的四边形是矩形
你能归纳矩形的判定方法吗?
四边形
平行
四边形
一个角
是直角
矩形
对角线
相等
矩形
三个角
是直角
矩形
矩形
对角线互相
平分且相等
整理归纳
分别测量出两组对边的长度和一个内角的度数,如果两组对边的长度分别相等,且这个内角是直角,则相框符合规格
测量出三个内角的度数,如果三个内角都是直角,则相框符合规格
分别测量出相框四边和两条对角线的长度,如果相框两组对边长度、两条对角线的长度分别相等,那么相框符合规格
方案:
方案:
方案:
实际应用
小丽和吴娟是怎样知道所买的相框是矩形的呢
判断
1.对角线相等的四边形是矩形。 ( )
2.对角线互相平分且相等的四边形是矩形。 ( )
3.有一个角是直角的四边形是矩形。 ( )
4.四个角都是直角的四边形是矩形。 ( )
5.四个角都相等的四边形是矩形。 ( )
6.对角线相等且有一个角是直角的四边形是矩形。 ( )
7.对角线相等且互相垂直的四边形是矩形。 ( )
8.两组对边分别平行,且对角线相等的四边形是矩形. ( )
辨一辨
例1 已知:如图,矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,
求证:四边形EFGH是矩形
证明:
∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵ E、F、G、H分别是AO、BO、CO、DO的中点
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角线互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形)。
例2:已知:如图,平行四边形ABCD的四个内角的平分线 ,分别相交于点E,F,G,H.
求证:四边形EFGH是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC
∴∠DAB+∠ABC=180°
又∵AE平分∠DAB,BG平分∠ABC
∴∠AFB=1800—(∠EAB+∠ABG)=90°
同理:∠AED=∠BGC=∠CHD=90°
四边形EFGH是矩形
∴∠EAB+∠ABG= ×180°=90°
∴∠EAB= ∠DAB, ∠ABG = ∠ABC
∴∠AED=∠BGC=∠ GFE =∠GHE=90°
课堂小结
今天这堂课你有什么收获?
四边形
平行
四边形
一个角
是直角
矩形
对角线
相等
矩形
三个角
是直角
矩形
矩形
对角线互相
平分且相等
1、渗透了类比的学习方法
2、体会了图形判定探究的一般思路
证明
逆命题
(修正)
性质
猜想
判定定理
1、教材习题18.2中第1、2、3题。
2、完成《基础训练》对应课时的习题。
课后作业
