人教版八年级数学下册第十九章 一次函数《一次函数与一元一次不等式》课件(共16张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十九章 一次函数《一次函数与一元一次不等式》课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 573.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
一次函数与一元一次不等式
问题 : 已知一次函数y=2x+6 (1)画出函数图象,并求它与x轴交点的坐标;
o
y
y=2x+6
x
B(-3,0)
A(0,6)
(3)观察图象,判断当x取什么值时,函数 值y=0
B(-3,0)
X= -3
温故知新
(2)函数的图象与x轴交点横坐标与一元一次方程2x+6=0的解有何关系
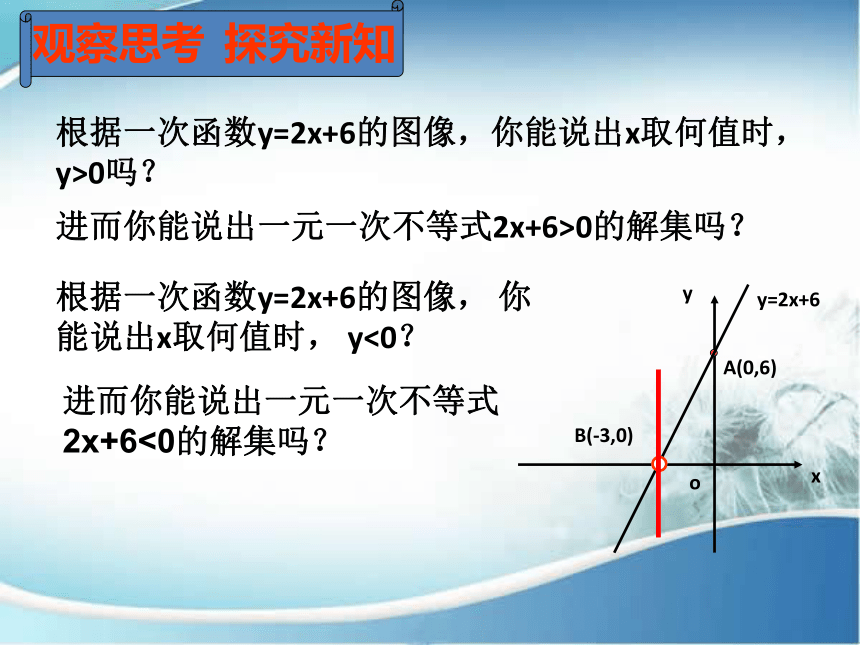
根据一次函数y=2x+6的图像, 你能说出x取何值时, y<0?
观察思考 探究新知
o
y
y=2x+6
x
B(-3,0)
A(0,6)
根据一次函数y=2x+6的图像,你能说出x取何值时,y>0吗?
进而你能说出一元一次不等式2x+6>0的解集吗?
进而你能说出一元一次不等式2x+6<0的解集吗?
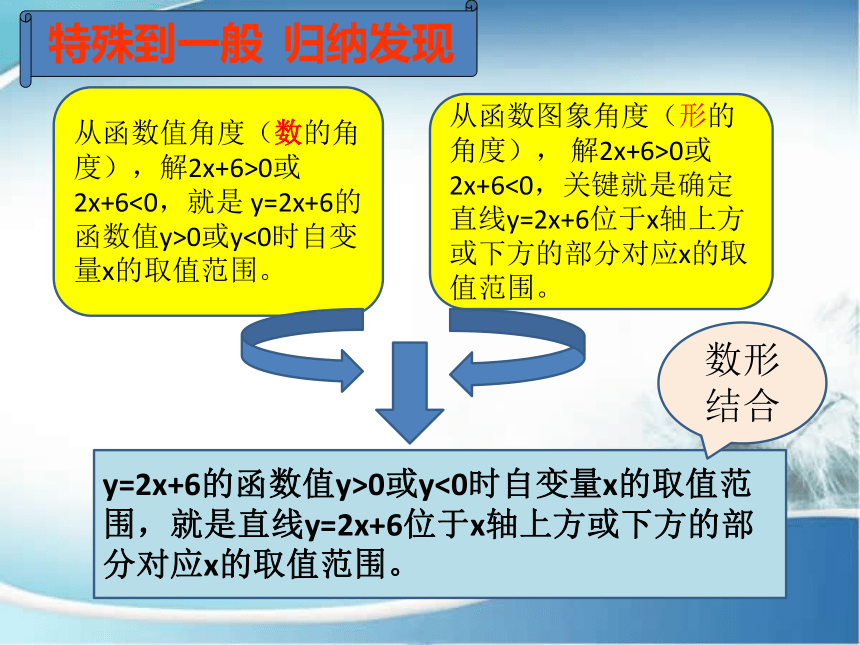
特殊到一般 归纳发现
从函数值角度(数的角度),解2x+6>0或2x+6<0,就是 y=2x+6的函数值y>0或y<0时自变量x的取值范围。
从函数图象角度(形的角度), 解2x+6>0或2x+6<0,关键就是确定直线y=2x+6位于x轴上方或下方的部分对应x的取值范围。
y=2x+6的函数值y>0或y<0时自变量x的取值范围,就是直线y=2x+6位于x轴上方或下方的部分对应x的取值范围。
数形结合
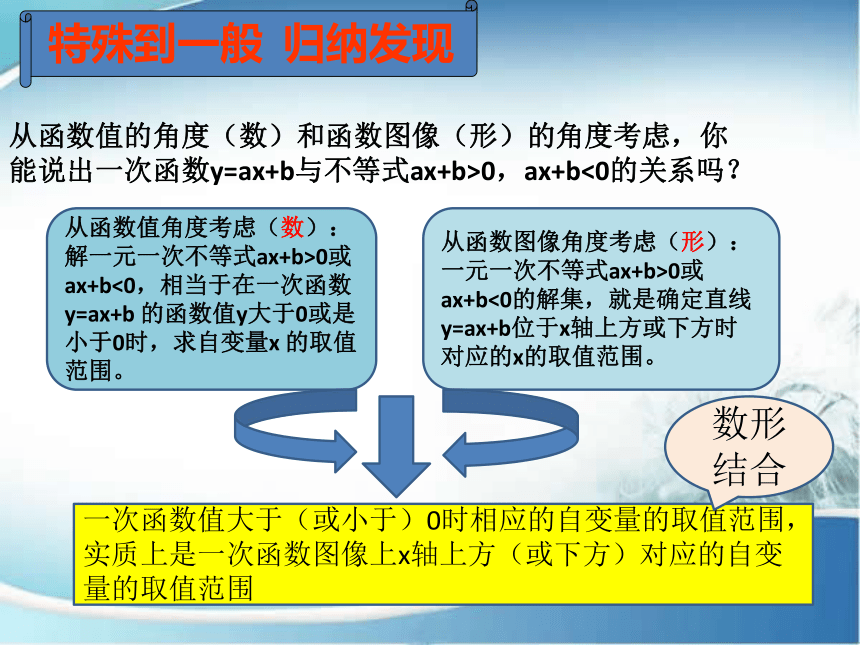
特殊到一般 归纳发现
从函数值的角度(数)和函数图像(形)的角度考虑,你能说出一次函数y=ax+b与不等式ax+b>0,ax+b<0的关系吗?
从函数值角度考虑(数):解一元一次不等式ax+b>0或ax+b<0,相当于在一次函数 y=ax+b 的函数值y大于0或是小于0时,求自变量x 的取值范围。
从函数图像角度考虑(形):一元一次不等式ax+b>0或ax+b<0的解集,就是确定直线y=ax+b位于x轴上方或下方时对应的x的取值范围。
一次函数值大于(或小于)0时相应的自变量的取值范围,实质上是一次函数图像上x轴上方(或下方)对应的自变量的取值范围
数形结合
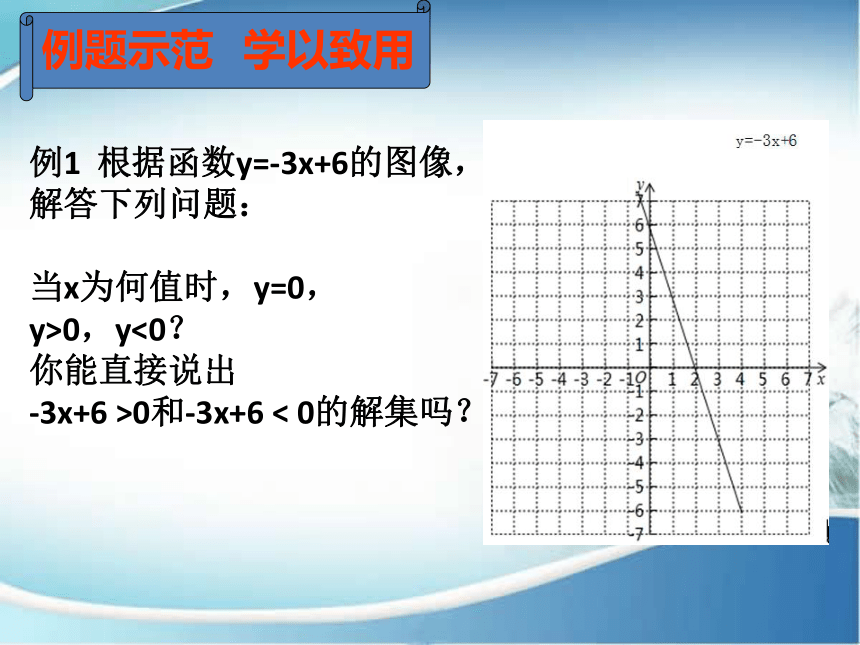
例1 根据函数y=-3x+6的图像,解答下列问题:
当x为何值时,y=0,
y>0,y<0?
你能直接说出
-3x+6 >0和-3x+6 < 0的解集吗?
例题示范 学以致用
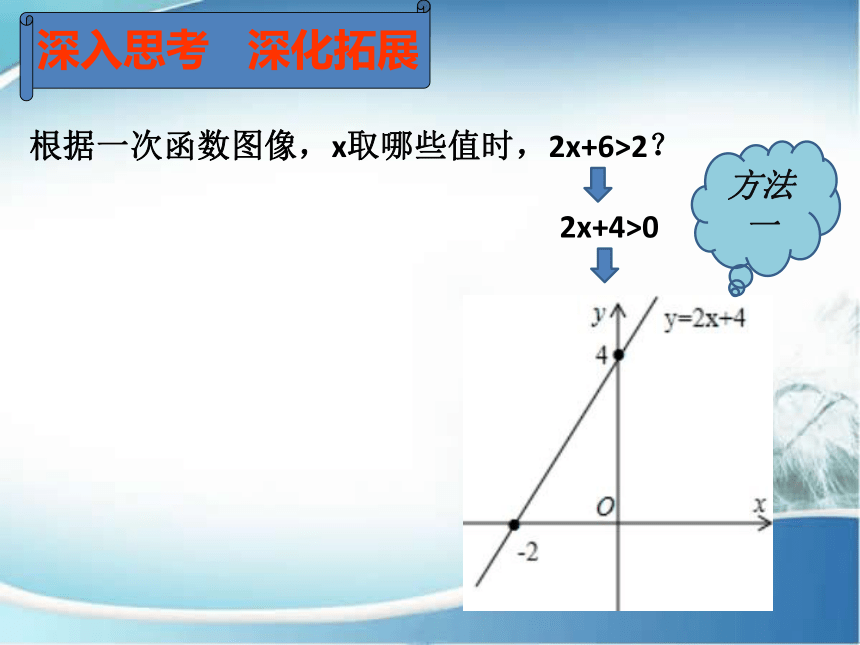
深入思考 深化拓展
根据一次函数图像,x取哪些值时,2x+6>2?
2x+4>0
方法一
深入思考 深化拓展
根据一次函数图像,x取哪些值时,2x+6>2?
方法二
例2 根据函数y=-3x+6的图像,解答下列问题:
求不等式-3x+6 >3的解集。
例题示范 学以致用
形成新知
因为任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0( ) 的形式,解这个一元一次不等式相当于求一次函数 y=ax+b 的函数值大于0或小于0时,自变量x的取值范围(从函数值角度考虑),也就是一次函数y=ax+b图像上x轴上方(或下方)对应的自变量x的取值范围(从函数图像的角度考虑)。
如图,根据一次函数y=-2x+4的图像观察,当函数值y>0时,x的取值范围为( )
基础训练 巩固应用
根据下列一次函数的图象,你能求出哪些不等式的解集?并直接说出相应不等式的解集.
y=-x+3
x
y
-2
0
y=3x+6
(1)
x
y
0
3
(2)
基础训练 巩固应用
(1)通过本节课的学习,你学到了什么知识?
(2)学完本堂课后,你最大的体验是什么?
归纳总结 反思提高
必做题:课本107页第5题,99页第13题
选做题:课本100页第15题
布置作业 反馈提高
如图,直线y=kx+b与x轴交于点A(-4,0),则当y>0时,x的取值范围是( )
A.x>-4 B.x>0
C.x<-4 D.x<0
拓展提升 发散思维
一次函数与一元一次不等式
问题 : 已知一次函数y=2x+6 (1)画出函数图象,并求它与x轴交点的坐标;
o
y
y=2x+6
x
B(-3,0)
A(0,6)
(3)观察图象,判断当x取什么值时,函数 值y=0
B(-3,0)
X= -3
温故知新
(2)函数的图象与x轴交点横坐标与一元一次方程2x+6=0的解有何关系
根据一次函数y=2x+6的图像, 你能说出x取何值时, y<0?
观察思考 探究新知
o
y
y=2x+6
x
B(-3,0)
A(0,6)
根据一次函数y=2x+6的图像,你能说出x取何值时,y>0吗?
进而你能说出一元一次不等式2x+6>0的解集吗?
进而你能说出一元一次不等式2x+6<0的解集吗?
特殊到一般 归纳发现
从函数值角度(数的角度),解2x+6>0或2x+6<0,就是 y=2x+6的函数值y>0或y<0时自变量x的取值范围。
从函数图象角度(形的角度), 解2x+6>0或2x+6<0,关键就是确定直线y=2x+6位于x轴上方或下方的部分对应x的取值范围。
y=2x+6的函数值y>0或y<0时自变量x的取值范围,就是直线y=2x+6位于x轴上方或下方的部分对应x的取值范围。
数形结合
特殊到一般 归纳发现
从函数值的角度(数)和函数图像(形)的角度考虑,你能说出一次函数y=ax+b与不等式ax+b>0,ax+b<0的关系吗?
从函数值角度考虑(数):解一元一次不等式ax+b>0或ax+b<0,相当于在一次函数 y=ax+b 的函数值y大于0或是小于0时,求自变量x 的取值范围。
从函数图像角度考虑(形):一元一次不等式ax+b>0或ax+b<0的解集,就是确定直线y=ax+b位于x轴上方或下方时对应的x的取值范围。
一次函数值大于(或小于)0时相应的自变量的取值范围,实质上是一次函数图像上x轴上方(或下方)对应的自变量的取值范围
数形结合
例1 根据函数y=-3x+6的图像,解答下列问题:
当x为何值时,y=0,
y>0,y<0?
你能直接说出
-3x+6 >0和-3x+6 < 0的解集吗?
例题示范 学以致用
深入思考 深化拓展
根据一次函数图像,x取哪些值时,2x+6>2?
2x+4>0
方法一
深入思考 深化拓展
根据一次函数图像,x取哪些值时,2x+6>2?
方法二
例2 根据函数y=-3x+6的图像,解答下列问题:
求不等式-3x+6 >3的解集。
例题示范 学以致用
形成新知
因为任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0( ) 的形式,解这个一元一次不等式相当于求一次函数 y=ax+b 的函数值大于0或小于0时,自变量x的取值范围(从函数值角度考虑),也就是一次函数y=ax+b图像上x轴上方(或下方)对应的自变量x的取值范围(从函数图像的角度考虑)。
如图,根据一次函数y=-2x+4的图像观察,当函数值y>0时,x的取值范围为( )
基础训练 巩固应用
根据下列一次函数的图象,你能求出哪些不等式的解集?并直接说出相应不等式的解集.
y=-x+3
x
y
-2
0
y=3x+6
(1)
x
y
0
3
(2)
基础训练 巩固应用
(1)通过本节课的学习,你学到了什么知识?
(2)学完本堂课后,你最大的体验是什么?
归纳总结 反思提高
必做题:课本107页第5题,99页第13题
选做题:课本100页第15题
布置作业 反馈提高
如图,直线y=kx+b与x轴交于点A(-4,0),则当y>0时,x的取值范围是( )
A.x>-4 B.x>0
C.x<-4 D.x<0
拓展提升 发散思维
