7.1.2 平面直角坐标系 课件(共19张PPT)
文档属性
| 名称 | 7.1.2 平面直角坐标系 课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-07 21:46:38 | ||
图片预览



文档简介
(共19张PPT)
第七章 平面直角坐标系
7.1 平面直角坐标系
7.1.2 平面直角坐标系
【问题2】如图,你能说出数轴上点A和点B的坐标吗?
【问题1】请你画出一条数轴.你能说出数轴的三要素吗?
【问题4】我们利用数轴可以确定直线上点的位置,能不能找到一种办法来确定平面内点的位置呢?
【问题3】已知数轴上点C的坐标是5,点D的坐标是-2,你能在数轴上画出点C和点D吗?
.
.
C
D
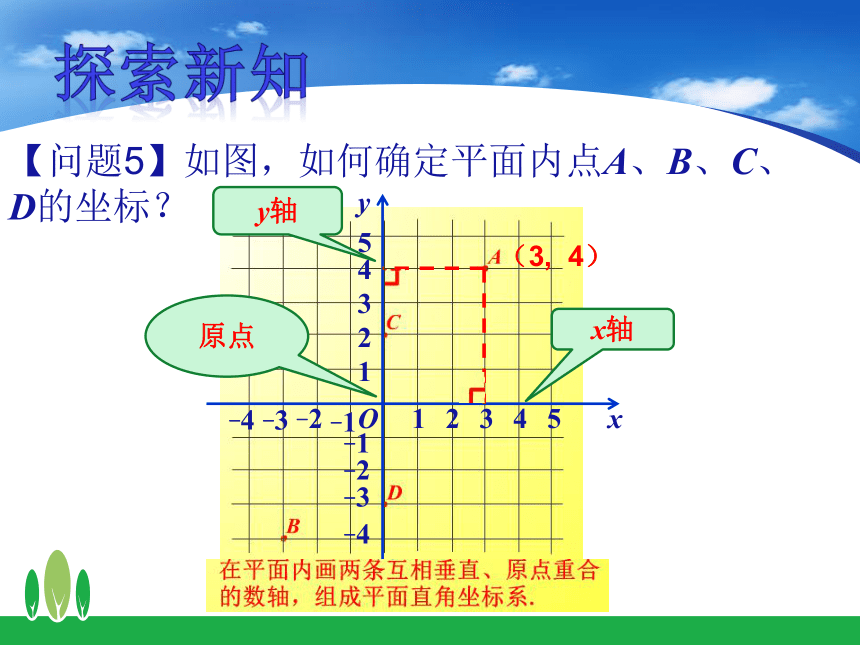
【问题5】如图,如何确定平面内点A、B、C、D的坐标?
O
2
4
-1
x
y
1
1
2
3
3
4
5
5
-4
-4
-3
-3
-2
-2
-1
x轴
y轴
原点
(3, 4)
O
2
4
-1
x
y
1
1
2
3
3
4
5
5
-4
-4
-3
-3
-2
-2
-1
x轴
y轴
原点
(3, 4)
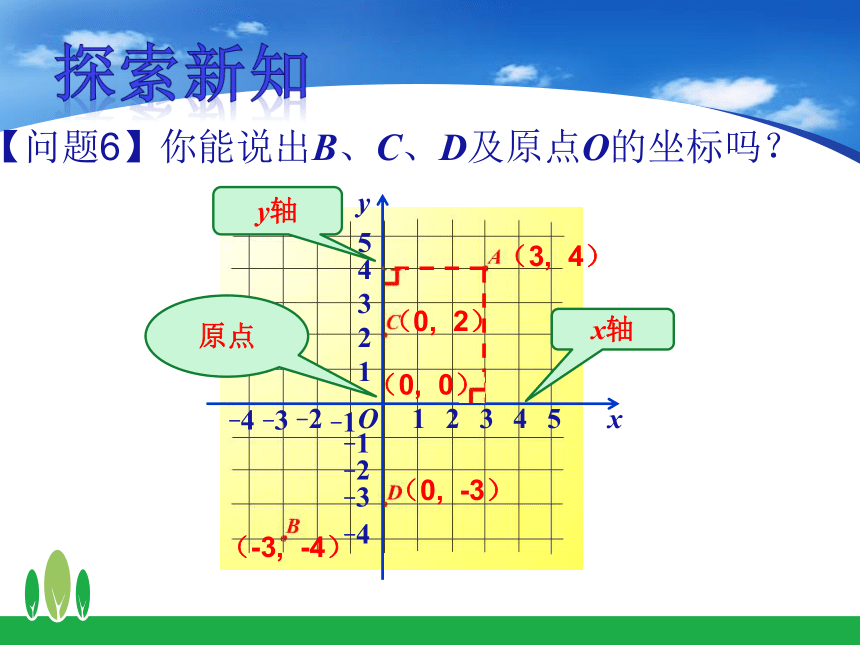
【问题6】你能说出B、C、D及原点O的坐标吗?
(-3, -4)
(0, -3)
(0, 2)
(0, 0)
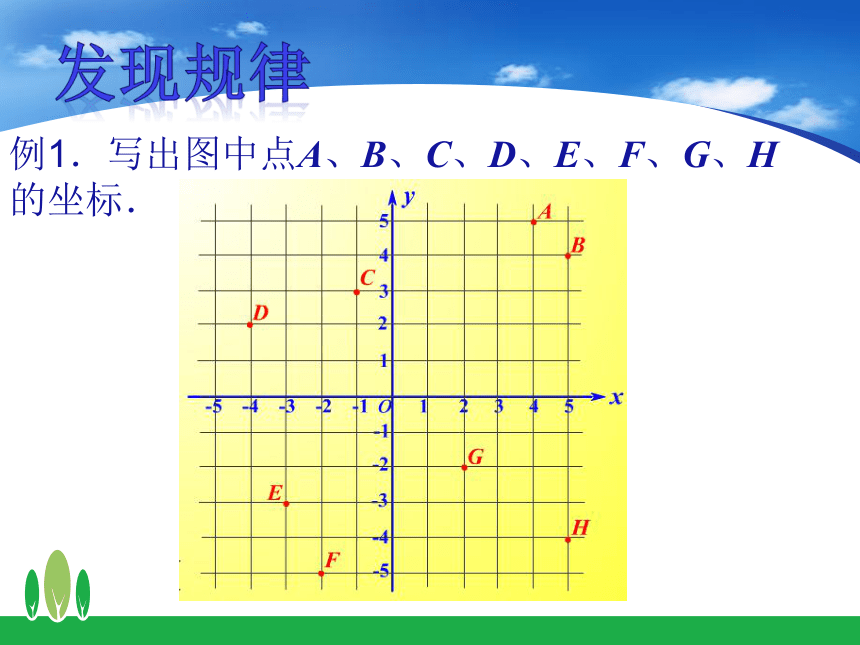
例1.写出图中点A、B、C、D、E、F、G、H的坐标.
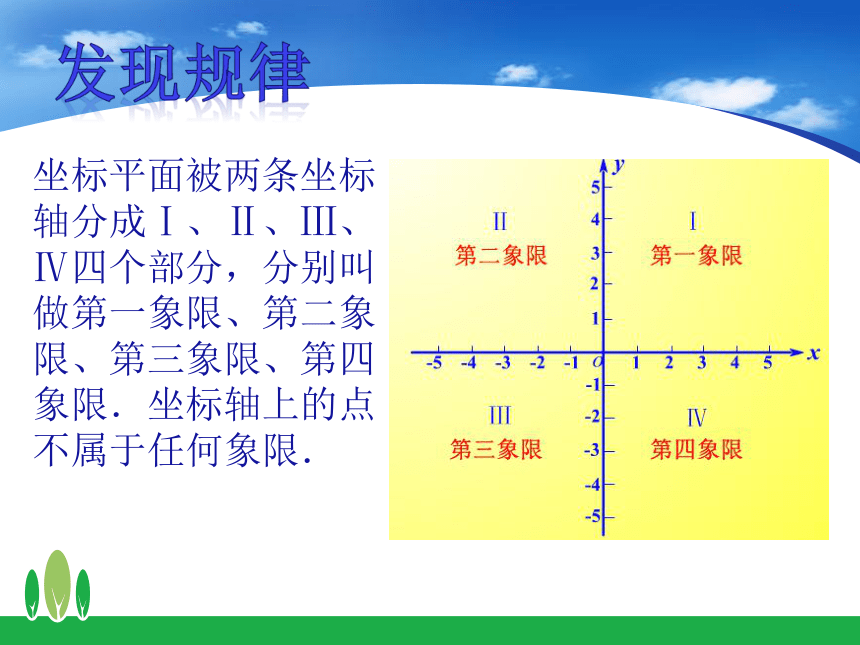
坐标平面被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做第一象限、第二象限、第三象限、第四象限.坐标轴上的点不属于任何象限.
【问题7】四个象限内点的坐标的符号有什么规律?
(+, +)
(-, +)
(-, -)
(+, -)
例2.在平面直角坐标系中描出下列各点:
M(1,0)、N(-3,0)、P(0,3)、Q(0,-4)、R(0,0).
【问题8】坐标轴上点的坐标有什么规律?
(4)原点既在x轴上,又在y轴上,是x轴和y轴的交点.
(3)坐标轴上的点不属于任何象限.
(2)y轴上点的横坐标为0,
y轴正半轴上点的纵坐标为“+”,
y轴负半轴上点的纵坐标为“-”.
(1)x轴上点的纵坐标为0,
x轴正半轴上点的横坐标为“+”,
x轴负半轴上点的横坐标为“-”.
根据点所在的位置,用“+”“-”或“0”填表.
点的位置 横坐标符号 纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上 在正半轴上
在负半轴上
在y轴上 在正半轴上
在负半轴上
原点
+
+
+
+
0
0
+
+
0
0
0
0
-
-
-
-
-
-
练习1.如图,正方形ABCD的边长为6,如果以点A为原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A,B,C,D的坐标.
y轴是AD所在的直线.
A(0,0)
B(6,0)
C(6,6)
D(0,6)
O
2
4
x
y
1
1
2
3
3
4
5
5
6
6
请另建立一个平面直角坐标系,这时正方形的顶点A,B,C,D的坐标又分别是多少?与同学交流一下.
练习2.填空:
(1)横坐标为正数的点在 象限;
(2)横坐标为负数的点在 象限;
(3)纵坐标为正数的点在 象限;
(4)纵坐标为负数的点在 象限;
(5)P(x,y)的坐标满足xy>0,则点P在 象限;
(6)P(x,y)的坐标满足xy<0,则点P在 象限.
第一或第四
第二或第三
第一或第二
第三或第四
第一或第三
第二或第四
练习3.填空:
(1)点A在y轴上,距离原点2个单位长度,点A的坐标是 ;
(2)点B在x轴上,距离原点6个单位长度,点B的坐标是 ;
(3)点C在y轴上,位于原点下方,距离原点1个单位长度,点C的坐标是 ;
(4)点D在x轴上方,y轴右侧,距离每条坐标轴都是3个单位长度,点D的坐标是 ;
(5)到x轴距离为5,到y轴距离为4的点的坐标为 .
(6,0)或(-6,0)
(0,2)或(0,-2)
(0,-1)
(3,3)
(4,5)或(4,-5)或(-4,5)或(-4,-5)
1.
x
y
O
2.
3.能建立适当的直角坐标系描述点的坐标.
4.数形结合的思想.
必做作业:
1.教材第68页练习第1、2题.
2.教材习题7.1第3、4、5、6题.
选做作业:
教材习题7.1综合运用第8、9题.
第七章 平面直角坐标系
7.1 平面直角坐标系
7.1.2 平面直角坐标系
【问题2】如图,你能说出数轴上点A和点B的坐标吗?
【问题1】请你画出一条数轴.你能说出数轴的三要素吗?
【问题4】我们利用数轴可以确定直线上点的位置,能不能找到一种办法来确定平面内点的位置呢?
【问题3】已知数轴上点C的坐标是5,点D的坐标是-2,你能在数轴上画出点C和点D吗?
.
.
C
D
【问题5】如图,如何确定平面内点A、B、C、D的坐标?
O
2
4
-1
x
y
1
1
2
3
3
4
5
5
-4
-4
-3
-3
-2
-2
-1
x轴
y轴
原点
(3, 4)
O
2
4
-1
x
y
1
1
2
3
3
4
5
5
-4
-4
-3
-3
-2
-2
-1
x轴
y轴
原点
(3, 4)
【问题6】你能说出B、C、D及原点O的坐标吗?
(-3, -4)
(0, -3)
(0, 2)
(0, 0)
例1.写出图中点A、B、C、D、E、F、G、H的坐标.
坐标平面被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做第一象限、第二象限、第三象限、第四象限.坐标轴上的点不属于任何象限.
【问题7】四个象限内点的坐标的符号有什么规律?
(+, +)
(-, +)
(-, -)
(+, -)
例2.在平面直角坐标系中描出下列各点:
M(1,0)、N(-3,0)、P(0,3)、Q(0,-4)、R(0,0).
【问题8】坐标轴上点的坐标有什么规律?
(4)原点既在x轴上,又在y轴上,是x轴和y轴的交点.
(3)坐标轴上的点不属于任何象限.
(2)y轴上点的横坐标为0,
y轴正半轴上点的纵坐标为“+”,
y轴负半轴上点的纵坐标为“-”.
(1)x轴上点的纵坐标为0,
x轴正半轴上点的横坐标为“+”,
x轴负半轴上点的横坐标为“-”.
根据点所在的位置,用“+”“-”或“0”填表.
点的位置 横坐标符号 纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上 在正半轴上
在负半轴上
在y轴上 在正半轴上
在负半轴上
原点
+
+
+
+
0
0
+
+
0
0
0
0
-
-
-
-
-
-
练习1.如图,正方形ABCD的边长为6,如果以点A为原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A,B,C,D的坐标.
y轴是AD所在的直线.
A(0,0)
B(6,0)
C(6,6)
D(0,6)
O
2
4
x
y
1
1
2
3
3
4
5
5
6
6
请另建立一个平面直角坐标系,这时正方形的顶点A,B,C,D的坐标又分别是多少?与同学交流一下.
练习2.填空:
(1)横坐标为正数的点在 象限;
(2)横坐标为负数的点在 象限;
(3)纵坐标为正数的点在 象限;
(4)纵坐标为负数的点在 象限;
(5)P(x,y)的坐标满足xy>0,则点P在 象限;
(6)P(x,y)的坐标满足xy<0,则点P在 象限.
第一或第四
第二或第三
第一或第二
第三或第四
第一或第三
第二或第四
练习3.填空:
(1)点A在y轴上,距离原点2个单位长度,点A的坐标是 ;
(2)点B在x轴上,距离原点6个单位长度,点B的坐标是 ;
(3)点C在y轴上,位于原点下方,距离原点1个单位长度,点C的坐标是 ;
(4)点D在x轴上方,y轴右侧,距离每条坐标轴都是3个单位长度,点D的坐标是 ;
(5)到x轴距离为5,到y轴距离为4的点的坐标为 .
(6,0)或(-6,0)
(0,2)或(0,-2)
(0,-1)
(3,3)
(4,5)或(4,-5)或(-4,5)或(-4,-5)
1.
x
y
O
2.
3.能建立适当的直角坐标系描述点的坐标.
4.数形结合的思想.
必做作业:
1.教材第68页练习第1、2题.
2.教材习题7.1第3、4、5、6题.
选做作业:
教材习题7.1综合运用第8、9题.
