青岛版七年级数学下册课件:三元一次方程组 (共29张PPT)
文档属性
| 名称 | 青岛版七年级数学下册课件:三元一次方程组 (共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 18:04:14 | ||
图片预览







文档简介
(共29张PPT)
基础课堂·精讲精练
提升拓展·考向导练
课堂小结·名师点金
三元一次方程组
精炼方法·教你一招
1
三元一次方程(组)的有关概念
基础课堂·精讲精练
精 讲
1.三元一次方程:含有_____未知数,并且含有未知数
的项的次数都是___,像这样的方程叫做三元一次方程.
必备条件:
(1)是_____方程;(2)含_____未知数;(3)含未知数的
项的次数都是____.
2.三元一次方程组:含有三个未知数,每个方程中含
未知数的项的次数都是1,并且一共有三个方程,
像这样的方程组叫做三元一次方程组.
三个
1
整式
三个
1
基础课堂·精讲精练
精 讲
必备条件:
(1)是整式方程;(2)含三个未知数;
(3)三个都是一次方程;(4)联立在一起.
3.易错警示:
(1)误认为三元一次方程组中每个方程必须是三元一
次方程,实际上只需方程组中共有三个未知数即可;
(2)把含有未知数的项的次数为1误认为未知数的次
数为1.
基础课堂·精讲精练
精 练
1
三元一次方程(组)的有关概念
1.下列方程是三元一次方程的是________.
(填序号)
①x+y-z=1 ②4xy+3z=7
③ +y-7z=0 ④6x+4y-3=0
①
基础课堂·精讲精练
精 练
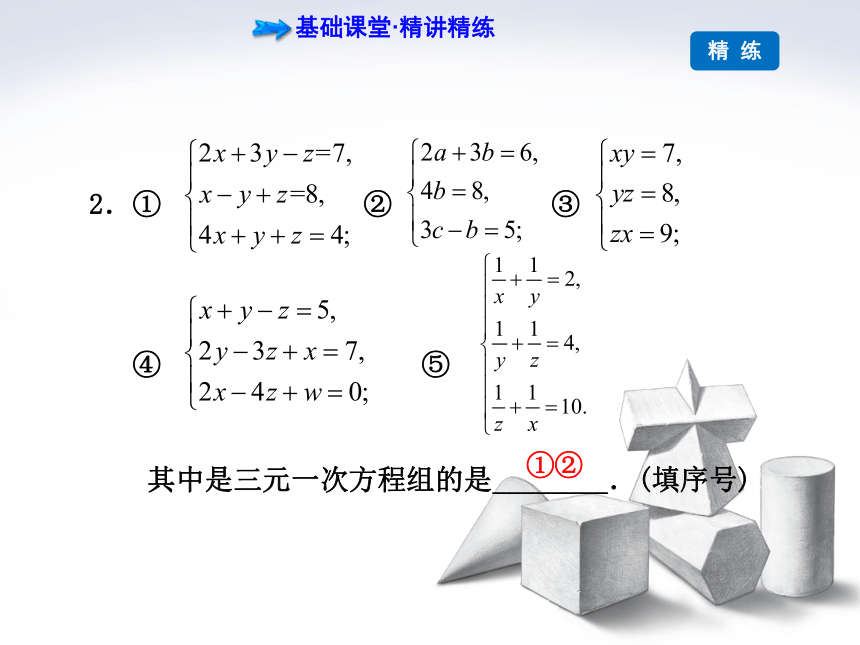
2.① ② ③
④ ⑤
其中是三元一次方程组的是________.(填序号)
①②
基础课堂·精讲精练
精 练
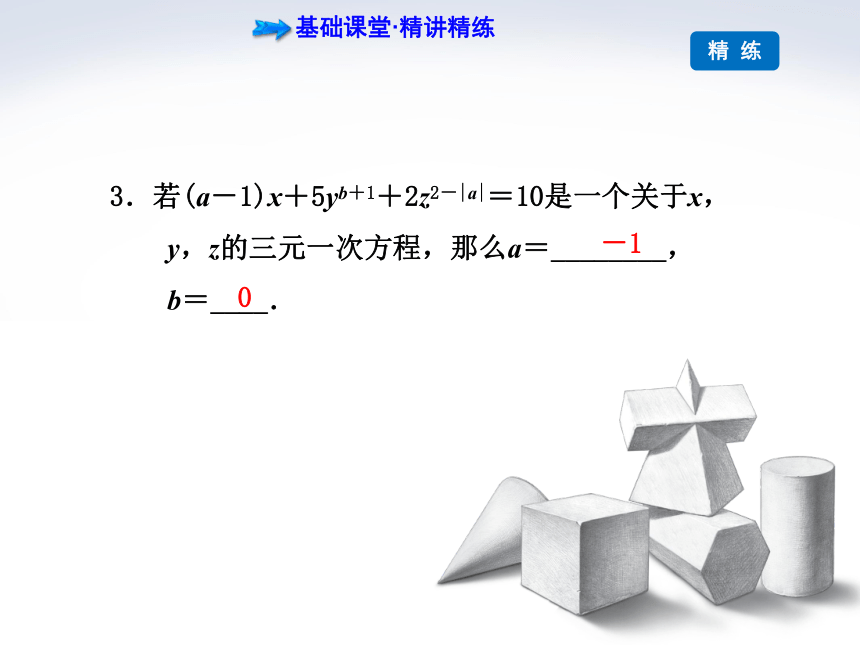
3.若(a-1)x+5yb+1+2z2-|a|=10是一个关于x,
y,z的三元一次方程,那么a=________,
b=____.
-1
0
2
三元一次方程组的解法
基础课堂·精讲精练
精 讲
1.解三元一次方程组的基本思路:通过“代入”或
“加减”进行消元,把“______”化为“_____”,
使三元一次方程组转化为二元一次方程组,进而
再转化为_________方程,用简图表示为:
三元一次方程组
二元一次方程组
一元一
次方程
消元
消元
三元
二元
一元一次
基础课堂·精讲精练
精 讲
2.求解方法:加减消元法和代入消元法.
3.解三元一次方程组的一般步骤:(1)利用代入法或
加减法消去三元一次方程组的一个未知数,得到
关于另外两个未知数的二元一次方程组;
(2)解这个二元一次方程组,求出两个未知数的值;
(3)将求得的两个未知数的值代入原方程组中的一个
系数比较简单的方程,得到一个一元一次方程;
(4)解这个一元一次方程,求出最后一个未知数的值;
(5)将求得的三个未知数的值用符号“{”合写在一
起.
基础课堂·精讲精练
精 练
2
三元一次方程组的解法
4.解三元一次方程组
先消去________,化为关于________、
_______ 的二元一次方程组较简便.
z
x
y
基础课堂·精讲精练
精 练
5.解方程组 若要使运算简便,消元
的方法应选( )
A.消去x B.消去y
C.消去z D.以上说法都不对
B
因为y的系数的绝对值都是1,所以消去y较简便.
基础课堂·精讲精练
精 练
6.已知三元一次方程组
经过步骤①-③和③×4+②消去未知数z后,得
到的二元一次方程组是( )
A. B.
C. D.
①
②
③
A
3
三元一次方程组的应用
基础课堂·精讲精练
精 讲
(1)弄清题意和题目中的数量关系,用字母(如
x,y,z)表示题目中的数量关系.
(2)找出能够表达应用题全部含义的三个相等关系.
(3)根据这些相等关系列出代数式,从而列出方程,
并组成方程组.
(4)解这个方程组求出未知数的值.
(5)写出答案,包括单位名称.
基础课堂·精讲精练
精 练
3
三元一次方程组的应用
7.(2015·滨州)某服装厂专门安排210名工人进行
手工衬衣的缝制,每件衬衣由2个衣袖、1个衣
身、1个衣领组成.如果每人每天能够缝制衣袖
10个,或衣身15个,或衣领12个,那么应该安
排________名工人缝制衣袖,才能使每天缝制
出的衣袖、衣身、衣领正好配套.
120
忽略集中消同一未知数导致不会解三元一次方程组
基础课堂·精讲精练
1
精 练
8.下面是小明解三元一次方程组的消元过程,当他
解到第三步时,发现还是无法求出方程组的解,
请帮小明分析解题的错因,并加以改正.
解方程组:
[错解]第一步:①-②,得(消y)x-z=-6④,第
二步:②-③,得(消z)y-x=3⑤,第三步:由④
⑤组成方程组,得 此方程组
无法求解.
①
②
③
基础课堂·精讲精练
精 练
错解原因是消元的目的不明确,消元时,应始终对同一个未知数进行,否则就达不到消元的目的.
正解:②-③,得y-x=3,④,
由①④组成方程组,得
解得 将x=12代入③,得z=18.
∴方程组的解为
加减消元时,易漏乘某项系数而出错
基础课堂·精讲精练
2
精 练
9.解方程组
①
②
③
由②+①×2,得4x+3x+6z+2z=4,
即7x+8z=4.④,
由③+②×2,得6x-4x+4z-z=4-1,
即2x+3z=3.⑤
基础课堂·精讲精练
精 练
由④⑤组成方程组,得
解得 把 代入①,得y=-2.
所以原方程组的解为
解三元一次方程组时,通常需在某些方程两边同乘以某常数,以便于消去同一未知数;在变形过程中,易漏乘常数项而出现方程①变形为4x+2y+6z=1的错误.
课堂小结·名师点金
名师点金
解三元一次方程组的基本思路仍是消元,是将复杂问题简单化的一种方法.其目的是利用代入法或加减法消去一个未知数,从而变三元为二元,然后解这个二元一次方程组,求出两个未知数,最后再求出另一个未知数.其基本过程为:
三元 二元 一元.
消元
消元
转化
转化
1
巧解较复杂的三元方程组(换元法)
提升拓展·考向导练
10.解方程组
①
②
③
分析
此方程组较为复杂,通过观察各个方程可以发现将 , , 分别看成一个整体,则方程可化为三元一次方程组,再通过三元一次方程组的解法可求解.
提升拓展·考向导练
设 =a, =b, =c,
则原方程组可化为
①+②,得2a+2c=1,④
②+③,得2a+4c=4.⑤
④与⑤组成方程组,得
解这个方程组,得
①
②
③
提升拓展·考向导练
把 代入①,得b=6.
因此,x=-1,y= ,z= .
即原方程组的解为
本题运用了换元法,将 , , 分别用a,b,c表示,将原方程组化为关于a,b,c的三元一次方程组,求出a,b,c的值后,进一步再求x,y,z的值,这种方法可使解题过程变简便.
2
巧解含比例的三元方程组(等比法)
提升拓展·考向导练
11.解方程组
①
②
设x=k,y=2k,z=3k,代入②得:
2k+2k-9k=15.解得k=-3.
∴原方程组的解为
像这种已知未知数之间数量比的问题,通常采用设参数的方法,将“多元”化为“一元”,使解题过程变简便.
3
巧解“每个方程中只有二元”的三元一次方程组(整体思想)
提升拓展·考向导练
12.解方程组:
①
②
③
①+②+③得:2x+2y+2z=12,
所以x+y+z=6,④
④-①,得z=3.④-②,得x=1.④-③,得y=2.
所以原方程组的解为
本题没有采用常规的消元方法求解,而是利用整体加减的方法求出未知数的值,给解题过程带来了简便.
4
代入法、加减法的综合运用(一题多解)
提升拓展·考向导练
13.用两种消元法解方程组:
①
②
③
方法一:代入法解方程组.
把②变形为:2y=3x-4z-8,④
将④代入①得:2x+2(3x-4z-8)-3z=9,整理得
8x-11z=25.⑤
将④代入③得:5x-3(3x-4z-8)-5z=7,整理得
4x-7z=17.⑥
由⑤⑥组成方程组,得 解得
提升拓展·考向导练
将 代入④,得 y= .
∴此方程组的解为
方法二:加减法解方程组
①+②×2得:8x-11z=25.④
①×3+③×2得:16x-19z=41.⑤
由④、⑤,得 解得
将 代入①,得 y= .
∴此方程组的解为
5
利用三元一次方程组求有关式子的待定系数
提升拓展·考向导练
14.当x=1,-1,3时,y=ax2+bx+c的值分别为1,
4,0,求当x=2时,y的值.
由题意得: 解得
∴y= x2- x+ .
当x=2时,y= ×22- ×2+
=1-3+
= .
6
利用方程组解实际应用问题
提升拓展·考向导练
15.有三块牧场,草长得一样密一样快,面积分别
为3 公顷,10公顷和24公顷,第一块12头牛可
吃4星期,第二块21头牛可吃9星期,第三块可供
多少头牛吃18个星期?
设牧场每公顷原有草 x t,每星期新生草 y t,每头牛每周吃草a t,
根据题意得
提升拓展·考向导练
化简得:
②-①得,50y=45a,∴y=0.9a,
将y=0.9a代入①得10x+40×0.9a=144a,
∴x=10.8a,
∴
∴
答:第三块牧场可供36头牛吃18个星期.
②
①
精炼方法·教你一招
教你一招
解三元一次方程组的消元技巧:
(1)先消去某个方程缺少的未知数;
(2)先消去系数最简单的未知数;
(3)先消去系数成整倍数关系的未知数.
另外,在“消元”的过程中必须保证每个方程至少用一次.
基础课堂·精讲精练
提升拓展·考向导练
课堂小结·名师点金
三元一次方程组
精炼方法·教你一招
1
三元一次方程(组)的有关概念
基础课堂·精讲精练
精 讲
1.三元一次方程:含有_____未知数,并且含有未知数
的项的次数都是___,像这样的方程叫做三元一次方程.
必备条件:
(1)是_____方程;(2)含_____未知数;(3)含未知数的
项的次数都是____.
2.三元一次方程组:含有三个未知数,每个方程中含
未知数的项的次数都是1,并且一共有三个方程,
像这样的方程组叫做三元一次方程组.
三个
1
整式
三个
1
基础课堂·精讲精练
精 讲
必备条件:
(1)是整式方程;(2)含三个未知数;
(3)三个都是一次方程;(4)联立在一起.
3.易错警示:
(1)误认为三元一次方程组中每个方程必须是三元一
次方程,实际上只需方程组中共有三个未知数即可;
(2)把含有未知数的项的次数为1误认为未知数的次
数为1.
基础课堂·精讲精练
精 练
1
三元一次方程(组)的有关概念
1.下列方程是三元一次方程的是________.
(填序号)
①x+y-z=1 ②4xy+3z=7
③ +y-7z=0 ④6x+4y-3=0
①
基础课堂·精讲精练
精 练
2.① ② ③
④ ⑤
其中是三元一次方程组的是________.(填序号)
①②
基础课堂·精讲精练
精 练
3.若(a-1)x+5yb+1+2z2-|a|=10是一个关于x,
y,z的三元一次方程,那么a=________,
b=____.
-1
0
2
三元一次方程组的解法
基础课堂·精讲精练
精 讲
1.解三元一次方程组的基本思路:通过“代入”或
“加减”进行消元,把“______”化为“_____”,
使三元一次方程组转化为二元一次方程组,进而
再转化为_________方程,用简图表示为:
三元一次方程组
二元一次方程组
一元一
次方程
消元
消元
三元
二元
一元一次
基础课堂·精讲精练
精 讲
2.求解方法:加减消元法和代入消元法.
3.解三元一次方程组的一般步骤:(1)利用代入法或
加减法消去三元一次方程组的一个未知数,得到
关于另外两个未知数的二元一次方程组;
(2)解这个二元一次方程组,求出两个未知数的值;
(3)将求得的两个未知数的值代入原方程组中的一个
系数比较简单的方程,得到一个一元一次方程;
(4)解这个一元一次方程,求出最后一个未知数的值;
(5)将求得的三个未知数的值用符号“{”合写在一
起.
基础课堂·精讲精练
精 练
2
三元一次方程组的解法
4.解三元一次方程组
先消去________,化为关于________、
_______ 的二元一次方程组较简便.
z
x
y
基础课堂·精讲精练
精 练
5.解方程组 若要使运算简便,消元
的方法应选( )
A.消去x B.消去y
C.消去z D.以上说法都不对
B
因为y的系数的绝对值都是1,所以消去y较简便.
基础课堂·精讲精练
精 练
6.已知三元一次方程组
经过步骤①-③和③×4+②消去未知数z后,得
到的二元一次方程组是( )
A. B.
C. D.
①
②
③
A
3
三元一次方程组的应用
基础课堂·精讲精练
精 讲
(1)弄清题意和题目中的数量关系,用字母(如
x,y,z)表示题目中的数量关系.
(2)找出能够表达应用题全部含义的三个相等关系.
(3)根据这些相等关系列出代数式,从而列出方程,
并组成方程组.
(4)解这个方程组求出未知数的值.
(5)写出答案,包括单位名称.
基础课堂·精讲精练
精 练
3
三元一次方程组的应用
7.(2015·滨州)某服装厂专门安排210名工人进行
手工衬衣的缝制,每件衬衣由2个衣袖、1个衣
身、1个衣领组成.如果每人每天能够缝制衣袖
10个,或衣身15个,或衣领12个,那么应该安
排________名工人缝制衣袖,才能使每天缝制
出的衣袖、衣身、衣领正好配套.
120
忽略集中消同一未知数导致不会解三元一次方程组
基础课堂·精讲精练
1
精 练
8.下面是小明解三元一次方程组的消元过程,当他
解到第三步时,发现还是无法求出方程组的解,
请帮小明分析解题的错因,并加以改正.
解方程组:
[错解]第一步:①-②,得(消y)x-z=-6④,第
二步:②-③,得(消z)y-x=3⑤,第三步:由④
⑤组成方程组,得 此方程组
无法求解.
①
②
③
基础课堂·精讲精练
精 练
错解原因是消元的目的不明确,消元时,应始终对同一个未知数进行,否则就达不到消元的目的.
正解:②-③,得y-x=3,④,
由①④组成方程组,得
解得 将x=12代入③,得z=18.
∴方程组的解为
加减消元时,易漏乘某项系数而出错
基础课堂·精讲精练
2
精 练
9.解方程组
①
②
③
由②+①×2,得4x+3x+6z+2z=4,
即7x+8z=4.④,
由③+②×2,得6x-4x+4z-z=4-1,
即2x+3z=3.⑤
基础课堂·精讲精练
精 练
由④⑤组成方程组,得
解得 把 代入①,得y=-2.
所以原方程组的解为
解三元一次方程组时,通常需在某些方程两边同乘以某常数,以便于消去同一未知数;在变形过程中,易漏乘常数项而出现方程①变形为4x+2y+6z=1的错误.
课堂小结·名师点金
名师点金
解三元一次方程组的基本思路仍是消元,是将复杂问题简单化的一种方法.其目的是利用代入法或加减法消去一个未知数,从而变三元为二元,然后解这个二元一次方程组,求出两个未知数,最后再求出另一个未知数.其基本过程为:
三元 二元 一元.
消元
消元
转化
转化
1
巧解较复杂的三元方程组(换元法)
提升拓展·考向导练
10.解方程组
①
②
③
分析
此方程组较为复杂,通过观察各个方程可以发现将 , , 分别看成一个整体,则方程可化为三元一次方程组,再通过三元一次方程组的解法可求解.
提升拓展·考向导练
设 =a, =b, =c,
则原方程组可化为
①+②,得2a+2c=1,④
②+③,得2a+4c=4.⑤
④与⑤组成方程组,得
解这个方程组,得
①
②
③
提升拓展·考向导练
把 代入①,得b=6.
因此,x=-1,y= ,z= .
即原方程组的解为
本题运用了换元法,将 , , 分别用a,b,c表示,将原方程组化为关于a,b,c的三元一次方程组,求出a,b,c的值后,进一步再求x,y,z的值,这种方法可使解题过程变简便.
2
巧解含比例的三元方程组(等比法)
提升拓展·考向导练
11.解方程组
①
②
设x=k,y=2k,z=3k,代入②得:
2k+2k-9k=15.解得k=-3.
∴原方程组的解为
像这种已知未知数之间数量比的问题,通常采用设参数的方法,将“多元”化为“一元”,使解题过程变简便.
3
巧解“每个方程中只有二元”的三元一次方程组(整体思想)
提升拓展·考向导练
12.解方程组:
①
②
③
①+②+③得:2x+2y+2z=12,
所以x+y+z=6,④
④-①,得z=3.④-②,得x=1.④-③,得y=2.
所以原方程组的解为
本题没有采用常规的消元方法求解,而是利用整体加减的方法求出未知数的值,给解题过程带来了简便.
4
代入法、加减法的综合运用(一题多解)
提升拓展·考向导练
13.用两种消元法解方程组:
①
②
③
方法一:代入法解方程组.
把②变形为:2y=3x-4z-8,④
将④代入①得:2x+2(3x-4z-8)-3z=9,整理得
8x-11z=25.⑤
将④代入③得:5x-3(3x-4z-8)-5z=7,整理得
4x-7z=17.⑥
由⑤⑥组成方程组,得 解得
提升拓展·考向导练
将 代入④,得 y= .
∴此方程组的解为
方法二:加减法解方程组
①+②×2得:8x-11z=25.④
①×3+③×2得:16x-19z=41.⑤
由④、⑤,得 解得
将 代入①,得 y= .
∴此方程组的解为
5
利用三元一次方程组求有关式子的待定系数
提升拓展·考向导练
14.当x=1,-1,3时,y=ax2+bx+c的值分别为1,
4,0,求当x=2时,y的值.
由题意得: 解得
∴y= x2- x+ .
当x=2时,y= ×22- ×2+
=1-3+
= .
6
利用方程组解实际应用问题
提升拓展·考向导练
15.有三块牧场,草长得一样密一样快,面积分别
为3 公顷,10公顷和24公顷,第一块12头牛可
吃4星期,第二块21头牛可吃9星期,第三块可供
多少头牛吃18个星期?
设牧场每公顷原有草 x t,每星期新生草 y t,每头牛每周吃草a t,
根据题意得
提升拓展·考向导练
化简得:
②-①得,50y=45a,∴y=0.9a,
将y=0.9a代入①得10x+40×0.9a=144a,
∴x=10.8a,
∴
∴
答:第三块牧场可供36头牛吃18个星期.
②
①
精炼方法·教你一招
教你一招
解三元一次方程组的消元技巧:
(1)先消去某个方程缺少的未知数;
(2)先消去系数最简单的未知数;
(3)先消去系数成整倍数关系的未知数.
另外,在“消元”的过程中必须保证每个方程至少用一次.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
