北师大版八年级数学下册1.1第2课时 等腰三角形 教学设计(表格式)
文档属性
| 名称 | 北师大版八年级数学下册1.1第2课时 等腰三角形 教学设计(表格式) | 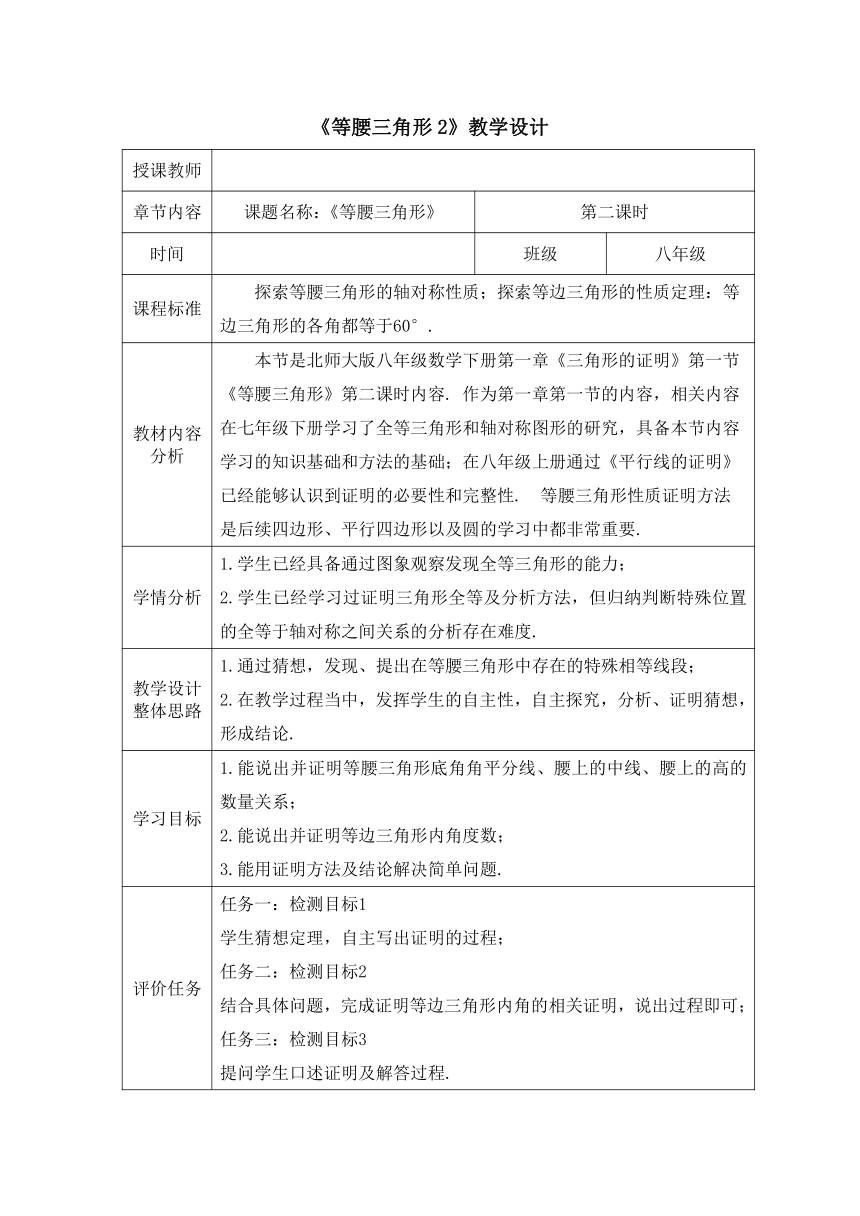 | |
| 格式 | docx | ||
| 文件大小 | 178.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 18:16:23 | ||
图片预览

文档简介
《等腰三角形2》教学设计
授课教师
章节内容 课题名称:《等腰三角形》 第二课时
时间 班级 八年级
课程标准 探索等腰三角形的轴对称性质;探索等边三角形的性质定理:等边三角形的各角都等于60°.
教材内容分析 本节是北师大版八年级数学下册第一章《三角形的证明》第一节《等腰三角形》第二课时内容. 作为第一章第一节的内容,相关内容在七年级下册学习了全等三角形和轴对称图形的研究,具备本节内容学习的知识基础和方法的基础;在八年级上册通过《平行线的证明》已经能够认识到证明的必要性和完整性. 等腰三角形性质证明方法是后续四边形、平行四边形以及圆的学习中都非常重要.
学情分析 1.学生已经具备通过图象观察发现全等三角形的能力; 2.学生已经学习过证明三角形全等及分析方法,但归纳判断特殊位置的全等于轴对称之间关系的分析存在难度.
教学设计整体思路 1.通过猜想,发现、提出在等腰三角形中存在的特殊相等线段; 2.在教学过程当中,发挥学生的自主性,自主探究,分析、证明猜想,形成结论.
学习目标 1.能说出并证明等腰三角形底角角平分线、腰上的中线、腰上的高的数量关系; 2.能说出并证明等边三角形内角度数; 3.能用证明方法及结论解决简单问题.
评价任务 任务一:检测目标1 学生猜想定理,自主写出证明的过程; 任务二:检测目标2 结合具体问题,完成证明等边三角形内角的相关证明,说出过程即可; 任务三:检测目标3 提问学生口述证明及解答过程.
教学环节 导入及教学过程
导入 问题导入: 我们研究等腰三角形(三角形)的问题时,一般围绕边、角、其它线段展开,尤其注重研究特殊的线段及其关系. 等腰三角形中,除了顶角的角平分线、底边上的高及底边中线外,还有哪些特殊的线段? 底角的角平分线、腰上的中线、腰上的高. 那么,这些线段之间是否具有特殊的关系呢? 对于等腰△ABC,AB=AC,你能在图中作出哪些相等的线段? 为什么这些线段是相等的呢?
活动1:指向目标1 证明:等腰三角形两底角的平分线相等. 已知:等腰△ABC,AB=AC,BD和CE是△ABC的角平分线. 求证:BD=CE. 证明:等腰三角形两腰上的中线相等. 已知:等腰△ABC,AB=AC,BD和CE是△ABC的中线. 求证:BD=CE. 证明:方法一:∵AD=AE,∠A=∠A,AB=AC. ∴△ABD≌△ACE. ∴BD=CE. 方法二:∵CD=BE,∠ABC=∠ACB,BC=CB. ∴△BCE≌△CBD. ∴BD=CE. 全等三角形是证明的基础方法. 证明:等腰三角形两腰上的高相等. 拓展:已知:等腰△ABC,AB=AC,点D和点E分别在边AB和AC上.若 那么:BD=CE是否相等? 若 那么BD=CE是否相等? 等腰三角形的这些特殊的线段相等与等腰三角形的轴对称性有何关系?
活动2:指向目标2 呈现评价任务: 证明:等边三角形三个内角相等,且每个角都等于60°. 已知:在△ABC中,AB=AC=BC. 求证:∠A=∠B=∠C=60°.
活动3:指向目标3 如图,在等边三角形ABC中,E、F分别在边AB、BC上,且AE=BF,AF与CE相交于点P. (1)求证:AF=CE;(2)求∠EPF的度数.
作业布置 A类作业:课本第6页随堂练习1-2题,课本第7页知识技能第1-2题. B类作业:课本第7页问题解决第4题.
授课教师
章节内容 课题名称:《等腰三角形》 第二课时
时间 班级 八年级
课程标准 探索等腰三角形的轴对称性质;探索等边三角形的性质定理:等边三角形的各角都等于60°.
教材内容分析 本节是北师大版八年级数学下册第一章《三角形的证明》第一节《等腰三角形》第二课时内容. 作为第一章第一节的内容,相关内容在七年级下册学习了全等三角形和轴对称图形的研究,具备本节内容学习的知识基础和方法的基础;在八年级上册通过《平行线的证明》已经能够认识到证明的必要性和完整性. 等腰三角形性质证明方法是后续四边形、平行四边形以及圆的学习中都非常重要.
学情分析 1.学生已经具备通过图象观察发现全等三角形的能力; 2.学生已经学习过证明三角形全等及分析方法,但归纳判断特殊位置的全等于轴对称之间关系的分析存在难度.
教学设计整体思路 1.通过猜想,发现、提出在等腰三角形中存在的特殊相等线段; 2.在教学过程当中,发挥学生的自主性,自主探究,分析、证明猜想,形成结论.
学习目标 1.能说出并证明等腰三角形底角角平分线、腰上的中线、腰上的高的数量关系; 2.能说出并证明等边三角形内角度数; 3.能用证明方法及结论解决简单问题.
评价任务 任务一:检测目标1 学生猜想定理,自主写出证明的过程; 任务二:检测目标2 结合具体问题,完成证明等边三角形内角的相关证明,说出过程即可; 任务三:检测目标3 提问学生口述证明及解答过程.
教学环节 导入及教学过程
导入 问题导入: 我们研究等腰三角形(三角形)的问题时,一般围绕边、角、其它线段展开,尤其注重研究特殊的线段及其关系. 等腰三角形中,除了顶角的角平分线、底边上的高及底边中线外,还有哪些特殊的线段? 底角的角平分线、腰上的中线、腰上的高. 那么,这些线段之间是否具有特殊的关系呢? 对于等腰△ABC,AB=AC,你能在图中作出哪些相等的线段? 为什么这些线段是相等的呢?
活动1:指向目标1 证明:等腰三角形两底角的平分线相等. 已知:等腰△ABC,AB=AC,BD和CE是△ABC的角平分线. 求证:BD=CE. 证明:等腰三角形两腰上的中线相等. 已知:等腰△ABC,AB=AC,BD和CE是△ABC的中线. 求证:BD=CE. 证明:方法一:∵AD=AE,∠A=∠A,AB=AC. ∴△ABD≌△ACE. ∴BD=CE. 方法二:∵CD=BE,∠ABC=∠ACB,BC=CB. ∴△BCE≌△CBD. ∴BD=CE. 全等三角形是证明的基础方法. 证明:等腰三角形两腰上的高相等. 拓展:已知:等腰△ABC,AB=AC,点D和点E分别在边AB和AC上.若 那么:BD=CE是否相等? 若 那么BD=CE是否相等? 等腰三角形的这些特殊的线段相等与等腰三角形的轴对称性有何关系?
活动2:指向目标2 呈现评价任务: 证明:等边三角形三个内角相等,且每个角都等于60°. 已知:在△ABC中,AB=AC=BC. 求证:∠A=∠B=∠C=60°.
活动3:指向目标3 如图,在等边三角形ABC中,E、F分别在边AB、BC上,且AE=BF,AF与CE相交于点P. (1)求证:AF=CE;(2)求∠EPF的度数.
作业布置 A类作业:课本第6页随堂练习1-2题,课本第7页知识技能第1-2题. B类作业:课本第7页问题解决第4题.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
