江苏省郑梁梅中学2012-2013学年高一上学期期末考试数学试题(带解析)
文档属性
| 名称 | 江苏省郑梁梅中学2012-2013学年高一上学期期末考试数学试题(带解析) |  | |
| 格式 | zip | ||
| 文件大小 | 176.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-31 17:11:39 | ||
图片预览




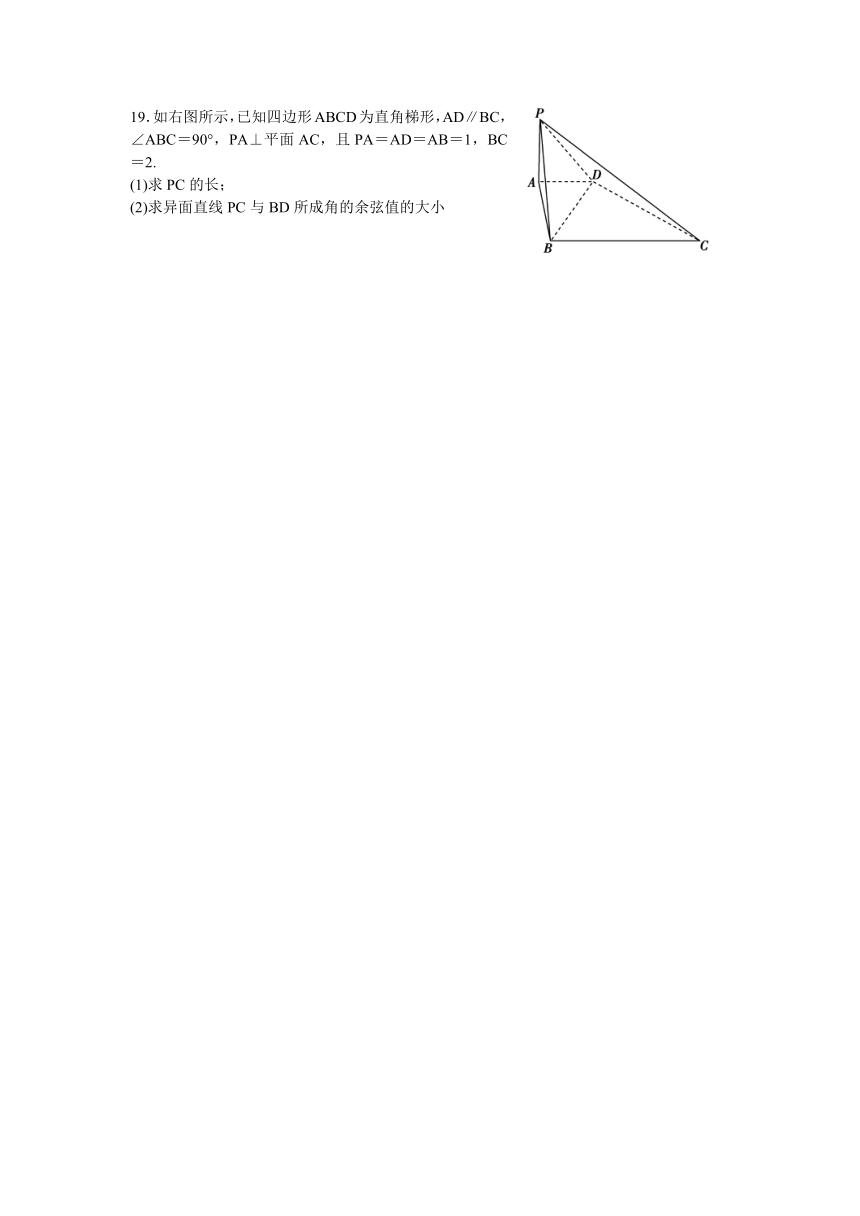
文档简介
郑梁梅中学2012-2013学年高一上学期期末考试数学试题
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、填空题
1.1.设集合,则=___ __.
2.不等式的解集是 .
3.用数字1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位上的数字之和为偶数的四位数共有 个(用数字作答)
4. 已知:若函数y=f(x)的定义域是[0,2],则函数g(x)=的定义域是_________.
5. 如图,在正方体ABCD-A1B1C1D1中,与面ABCD平行的面是____________.
6. 已知tan=则的值
7.小明的自行车用的是密码锁,密码锁的四位数密码由4个数字按一定顺序构成(数字不能重复),小明不小心忘记了密码中个数字的顺序,则随机输入由组成的一个四位数,不能打开锁的概率是_________.
8.在中,若,AB=5,AC=4,则的面积S=_________
9.随机变量服从正态分布"(0,1),若 P(<1) =0.8413 则P(-1<<0)=_____
10.在平面直角坐标系中,已知圆(为参数)和直线(为参数),则圆C的普通方程为 ,直线与圆C的位置关系是
11.设满足约束条件 ,若目标函数的最大值为8,则的最小值为
12.不等式的解集为_______________.
13.将4个相同的白球、5个相同的黑球、6个相同的红球放入4个不同盒子中的3个中,使得有1个空盒且其他3个盒子中球的颜色齐全的不同放法共有 种.(用数字作答)
14.设等差数列的前项和为,若对任意的等差数列及任意的正整
数都有不等式设等差数列的前项和为,若对任意的等差数列及任意的
正整数都有不等式成立,则实数的最大值成立,则实数的最大
值为
二、解答题
15.由经验得知,在某商场付款处排队等候付款的人数及概率如下表:
排队人数
0
1
2
3
4
5人以上
概率
0.1
0.16
0.3
0.3
0.1
0.04
(1)至多有2人排队的概率是多少? (2)至少有2人排队的概率是多少?
16.(12分)如图,在四棱椎中,底面是且边长为2的菱形,侧面为正三角形,其所在平面垂直于底面.
(1)若G为边的中点,求证:平面;
(2)求二面角的大小;
(3)若E为的中点,能否在棱上找一点F,使得平面平面,并证明你的结论.
17.若函数,
(1)当时,求函数的单调增区间;(2)函数是否存在极值.
18.(本题满分12分)
函数f (x)=x3+bx2+cx+d图象经过点(0,2),且在x=-1处的切线方程为6x - y+7=0.
(1)求函数f(x)解析式;
(2)求函数 f(x)的单调递减区间;
(3)求函数f(x)在[0,2]上的最大值和最小值.
19.如右图所示,已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2.
(1)求PC的长;
(2)求异面直线PC与BD所成角的余弦值的大小
20.(本题满分10分) 选修4—5:不等式选讲
(1)解关于x的不等式;
(2)若关于的不等式有解,求实数的取值范围.
参考答案
1.解:(1) 由得, 函数的定义域是
(2) 设, 则,
,
, ,
.
在上是减函数.
另解,为复合函数,设在为减函数,由于外层函数是增函数,所以在上是减函数.
(3) 当时, 有.
, 所以函数的值域是.
2.
3.324
4.
【解析】函数g(x)=的定义域需满足
5.面A1B1C1D1
6.3
7.
8.
9.0.3413
10.
11.4
【解析】
试题分析:画出可行域和目标函数,由图象可知,在处取到最大值,所以,所以
考点:本小题主要考查线性规划和基本不等式的综合应用,考查学生画图用图的能力.
点评:利用线性规划知识解题时,关键是准确画出可行域和目标函数.
12.
【解析】本试题主要是考查了绝对值不等式的求解。运用平方的思想得到一元二次不等式。
因为根据含有两个绝对值的不等式,可以移项,再平方,去掉绝对值符号得到
故不等式的解集为
解决该试题的关键是将原不等式两边平方,转换为一元二次不等式的解集。
13.720
【解析】
试题分析:本题可以分步来做:
第一步:首先从4个盒子中选取3个,共有4种取法;
第二步:假定选取了前三个盒子,则第四个为空,不予考虑。由于前三个盒子中的球必须同时包含黑白红三色,所以我们知道,每个盒子中至少有一个白球,一个黑球和一个红球。
第三步:①这样,白球还剩一个可以自由支配,它可以放在三个盒子中任意一个,共3种放法。②黑球还剩两个可以自由支配,这两个球可以分别放入三个盒子中的任意一个,这里有两种情况:一是两个球放入同一个盒子,有3种放法;二是两个球放入不同的两个盒子,有3种放法。综上,黑球共6种放法。③红球还剩三个可以自由支配,分三种情况:一是三个球放入同一个盒子,有3中放法。二是两个球放入同一个盒子,另外一个球放入另一个盒子,有6种放法。三是每个 盒子一个球,只有1种放法。综上,红球共10种放法。
所以总共有4×3×6×10=720种不同的放法。
考点:排列、组合;分布乘法原理;分类加法原理。
点评:本题考查排列、组合的运用,注意本题中同色的球是相同的。对于较难问题,我们可以采取分步来做。
14.
【解析】
试题分析:
因为,所以,令,则
而的最小值为,所以
考点:本小题主要考查等差数列的通项公式、前项和的计算和灵活应用,以及不等式
恒成立问题,考查学生转化问题的能力和运算求解能力.
点评:解决此题的关键在于将不等式转化为解答此类问题时要注意
灵活转化.
15.(1)0.56 (2)0.74
【解析】⑴设事件“有人排队”为,,“至多有2人排队”为事件B,“至少有2人排队”为事件C,则,,,,,,
⑵.
16.(1)同解析(2)二面角大小为,(3)同解析
【解析】(1),且是中点,所以
又为菱形,且,所以
所以
(2),
由三垂线定理得:为二面角的平面角,且
所以二面角大小为,
(3)连接相交于点,
在面中,过H点作交于F,
易证明面
17.(1)由题意,函数的定义域为 ………………1分
当时,, ……2分
令,即,得或 ………………4分
又因为,所以,函数的单调增区间为 ………………5分
(2) ……………6分
解法一:令,因为对称轴,所以只需考虑的正负,
当即时,在(0,+∞)上,
即在(0,+∞)单调递增,无极值 ………………8分
当即时,在(0,+∞)有解,所以函数存在极值.…10分
综上所述:当时,函数存在极值;当时,函数不存在极值.…12分
解法二:令即,记
当即时,, 在(0,+∞)单调递增,无极值 ………7分
当即时,解得:或
若则,列表如下:
(0,)
(,+∞)
—
0
+
↘
极小值
↗
由上表知:时函数取到极小值,即函数存在极小值。………9分
若,则,在(0,+∞)单调递减,不存在极值。……11分
综上所述,当时,函数存在极值,当时。函数不存在极值
18.(1)由f(0)=2得d=2.又切点(-1,1)在y=f(x)上 有-1+b-c+2=1,
又解得:b=-3,c=-3,d=2 …………5分
(2) ∵,
解 得函数的减区间为 …………9分
(3)由(2)知,函数在[0,2]上是减函数,
…………12分
19.(1)因为PA⊥平面AC,AB⊥BC,∴PB⊥BC,即∠PBC=90°,由勾股定理得PB==.
∴PC==.
(2)
如右图所示,过点C作CE∥BD交AD的延长线于E,连结PE,则∠PCE为异面直线PC与BD所成的角或它的补角.
∵CE=BD=,且PE==.
∴由余弦定理得cos∠PCE==-.
∴PC与BD所成角的余弦值为.
20.
解:设,则 …………4分
(1)2x(1≤3(x≤2,即x≥1时,不等式的解为1≤x≤2, …………6分
∴原不等式的解集为{x|x≤2}. …………7分
(2)由于x≥1时,函数y=2x(1是增函数,其最小值为f(1)=1,
当x<1时,,∴的最小值为1. …………9分
因为≤a有解,即≤a有解,所以a≥1. …………10分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、填空题
1.1.设集合,则=___ __.
2.不等式的解集是 .
3.用数字1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位上的数字之和为偶数的四位数共有 个(用数字作答)
4. 已知:若函数y=f(x)的定义域是[0,2],则函数g(x)=的定义域是_________.
5. 如图,在正方体ABCD-A1B1C1D1中,与面ABCD平行的面是____________.
6. 已知tan=则的值
7.小明的自行车用的是密码锁,密码锁的四位数密码由4个数字按一定顺序构成(数字不能重复),小明不小心忘记了密码中个数字的顺序,则随机输入由组成的一个四位数,不能打开锁的概率是_________.
8.在中,若,AB=5,AC=4,则的面积S=_________
9.随机变量服从正态分布"(0,1),若 P(<1) =0.8413 则P(-1<<0)=_____
10.在平面直角坐标系中,已知圆(为参数)和直线(为参数),则圆C的普通方程为 ,直线与圆C的位置关系是
11.设满足约束条件 ,若目标函数的最大值为8,则的最小值为
12.不等式的解集为_______________.
13.将4个相同的白球、5个相同的黑球、6个相同的红球放入4个不同盒子中的3个中,使得有1个空盒且其他3个盒子中球的颜色齐全的不同放法共有 种.(用数字作答)
14.设等差数列的前项和为,若对任意的等差数列及任意的正整
数都有不等式设等差数列的前项和为,若对任意的等差数列及任意的
正整数都有不等式成立,则实数的最大值成立,则实数的最大
值为
二、解答题
15.由经验得知,在某商场付款处排队等候付款的人数及概率如下表:
排队人数
0
1
2
3
4
5人以上
概率
0.1
0.16
0.3
0.3
0.1
0.04
(1)至多有2人排队的概率是多少? (2)至少有2人排队的概率是多少?
16.(12分)如图,在四棱椎中,底面是且边长为2的菱形,侧面为正三角形,其所在平面垂直于底面.
(1)若G为边的中点,求证:平面;
(2)求二面角的大小;
(3)若E为的中点,能否在棱上找一点F,使得平面平面,并证明你的结论.
17.若函数,
(1)当时,求函数的单调增区间;(2)函数是否存在极值.
18.(本题满分12分)
函数f (x)=x3+bx2+cx+d图象经过点(0,2),且在x=-1处的切线方程为6x - y+7=0.
(1)求函数f(x)解析式;
(2)求函数 f(x)的单调递减区间;
(3)求函数f(x)在[0,2]上的最大值和最小值.
19.如右图所示,已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2.
(1)求PC的长;
(2)求异面直线PC与BD所成角的余弦值的大小
20.(本题满分10分) 选修4—5:不等式选讲
(1)解关于x的不等式;
(2)若关于的不等式有解,求实数的取值范围.
参考答案
1.解:(1) 由得, 函数的定义域是
(2) 设, 则,
,
, ,
.
在上是减函数.
另解,为复合函数,设在为减函数,由于外层函数是增函数,所以在上是减函数.
(3) 当时, 有.
, 所以函数的值域是.
2.
3.324
4.
【解析】函数g(x)=的定义域需满足
5.面A1B1C1D1
6.3
7.
8.
9.0.3413
10.
11.4
【解析】
试题分析:画出可行域和目标函数,由图象可知,在处取到最大值,所以,所以
考点:本小题主要考查线性规划和基本不等式的综合应用,考查学生画图用图的能力.
点评:利用线性规划知识解题时,关键是准确画出可行域和目标函数.
12.
【解析】本试题主要是考查了绝对值不等式的求解。运用平方的思想得到一元二次不等式。
因为根据含有两个绝对值的不等式,可以移项,再平方,去掉绝对值符号得到
故不等式的解集为
解决该试题的关键是将原不等式两边平方,转换为一元二次不等式的解集。
13.720
【解析】
试题分析:本题可以分步来做:
第一步:首先从4个盒子中选取3个,共有4种取法;
第二步:假定选取了前三个盒子,则第四个为空,不予考虑。由于前三个盒子中的球必须同时包含黑白红三色,所以我们知道,每个盒子中至少有一个白球,一个黑球和一个红球。
第三步:①这样,白球还剩一个可以自由支配,它可以放在三个盒子中任意一个,共3种放法。②黑球还剩两个可以自由支配,这两个球可以分别放入三个盒子中的任意一个,这里有两种情况:一是两个球放入同一个盒子,有3种放法;二是两个球放入不同的两个盒子,有3种放法。综上,黑球共6种放法。③红球还剩三个可以自由支配,分三种情况:一是三个球放入同一个盒子,有3中放法。二是两个球放入同一个盒子,另外一个球放入另一个盒子,有6种放法。三是每个 盒子一个球,只有1种放法。综上,红球共10种放法。
所以总共有4×3×6×10=720种不同的放法。
考点:排列、组合;分布乘法原理;分类加法原理。
点评:本题考查排列、组合的运用,注意本题中同色的球是相同的。对于较难问题,我们可以采取分步来做。
14.
【解析】
试题分析:
因为,所以,令,则
而的最小值为,所以
考点:本小题主要考查等差数列的通项公式、前项和的计算和灵活应用,以及不等式
恒成立问题,考查学生转化问题的能力和运算求解能力.
点评:解决此题的关键在于将不等式转化为解答此类问题时要注意
灵活转化.
15.(1)0.56 (2)0.74
【解析】⑴设事件“有人排队”为,,“至多有2人排队”为事件B,“至少有2人排队”为事件C,则,,,,,,
⑵.
16.(1)同解析(2)二面角大小为,(3)同解析
【解析】(1),且是中点,所以
又为菱形,且,所以
所以
(2),
由三垂线定理得:为二面角的平面角,且
所以二面角大小为,
(3)连接相交于点,
在面中,过H点作交于F,
易证明面
17.(1)由题意,函数的定义域为 ………………1分
当时,, ……2分
令,即,得或 ………………4分
又因为,所以,函数的单调增区间为 ………………5分
(2) ……………6分
解法一:令,因为对称轴,所以只需考虑的正负,
当即时,在(0,+∞)上,
即在(0,+∞)单调递增,无极值 ………………8分
当即时,在(0,+∞)有解,所以函数存在极值.…10分
综上所述:当时,函数存在极值;当时,函数不存在极值.…12分
解法二:令即,记
当即时,, 在(0,+∞)单调递增,无极值 ………7分
当即时,解得:或
若则,列表如下:
(0,)
(,+∞)
—
0
+
↘
极小值
↗
由上表知:时函数取到极小值,即函数存在极小值。………9分
若,则,在(0,+∞)单调递减,不存在极值。……11分
综上所述,当时,函数存在极值,当时。函数不存在极值
18.(1)由f(0)=2得d=2.又切点(-1,1)在y=f(x)上 有-1+b-c+2=1,
又解得:b=-3,c=-3,d=2 …………5分
(2) ∵,
解 得函数的减区间为 …………9分
(3)由(2)知,函数在[0,2]上是减函数,
…………12分
19.(1)因为PA⊥平面AC,AB⊥BC,∴PB⊥BC,即∠PBC=90°,由勾股定理得PB==.
∴PC==.
(2)
如右图所示,过点C作CE∥BD交AD的延长线于E,连结PE,则∠PCE为异面直线PC与BD所成的角或它的补角.
∵CE=BD=,且PE==.
∴由余弦定理得cos∠PCE==-.
∴PC与BD所成角的余弦值为.
20.
解:设,则 …………4分
(1)2x(1≤3(x≤2,即x≥1时,不等式的解为1≤x≤2, …………6分
∴原不等式的解集为{x|x≤2}. …………7分
(2)由于x≥1时,函数y=2x(1是增函数,其最小值为f(1)=1,
当x<1时,,∴的最小值为1. …………9分
因为≤a有解,即≤a有解,所以a≥1. …………10分
同课章节目录
