北师大版八年级数学下册:第一章 三角形的证明1.2_第1课时_直角三角形 课件(共17张PPT)
文档属性
| 名称 | 北师大版八年级数学下册:第一章 三角形的证明1.2_第1课时_直角三角形 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 217.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 19:00:36 | ||
图片预览






文档简介
(共17张PPT)
2 直角三角形
第1课时
版 本:北京师范大学出版社
章 节:八年级下册第一章三角形的证明《直角三角形》(第1课时)
1.通过课本“想一想”会说出直角三角形的性质,并能解决相关问题.
2.通过例题证明,会说出直角三角形的判定方法,并能解决相关问题.
3.认识互逆命题、逆命题、互逆定理等概念,会说出一个命题的逆命题,并判断其真假.
学习目标
定理:有两个角互余的三角形是直角三角形.
定理:直角三角形的两个锐角互余.
(2)如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
(1)直角三角形的两个锐角又怎样的关系?为什么?
新知导入
算一算,猜一猜
已知在△ABC中,AB=c,BC=a,AC=b,
(1)填表:
a b c a2+b2与c2关系 三角形形状
3 4 5 ________ ______________
5 12 13 ________ ______________
8 15 17 ________ ______________
=
=
=
直角三角形
直角三角形
直角三角形
学习新知
图1 图2
(2)已知:如图1,在△ABC中,AB 2+AC 2=BC 2.
求证:△ABC是直角三角形.
学习新知
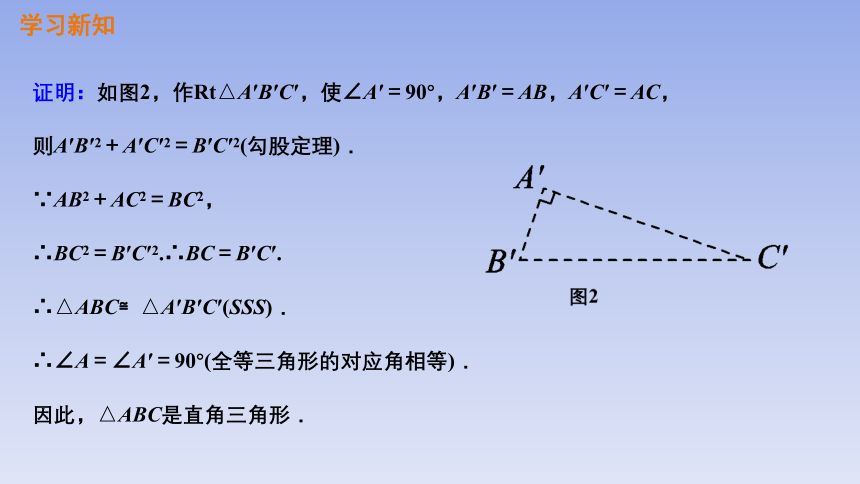
证明:如图2,作Rt△A′B′C′,使∠A′=90°,A′B′=AB,A′C′=AC,
则A′B′2+A′C′2=B′C′2(勾股定理).
∵AB2+AC2=BC2,
∴BC2=B′C′2.∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS).
∴∠A=∠A′=90°(全等三角形的对应角相等).
因此,△ABC是直角三角形.
学习新知
定理:
如果三角形两边的平方和等于第三边的平方,
那么这个三角形是________三角形.
直角
归纳总结
例1 如图所示,已知AB=4,BC=12,CD=13,DA=3,AB⊥AD,判断BC⊥BD是否成立,简述你的理由.
经典例题
解:BC⊥BD成立.理由如下:
在Rt△ABD中,∠BAD=90°,BD2=AB2+AD2=42+32=25.
又BD>0,
∴BD=5.
∵BD2+BC2=52+122=169=132=CD2,
∴∠DBC=90°,
∴BC⊥BD.
经典例题
勾股定理的逆定理 如果三角形两边的平方和等于第三边的平方,
那么这个三角形是直角三角形.
观察上面两个命题,它们的条件和结论之间有怎样的关系
在前面的学习中还有类似的命题吗
勾股定理的条件是第二个定理的结论,结论是第二个定理的条件..
勾股定理 在直角三角形中,两直角边的平方和等于斜边的平方.
想一想
1.如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角;
2.如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎;
3.一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等;
上面每组中两个命题的条件和结论也有类似的关系吗
与同伴交流.
想一想
在两个命题中,如果一个命题的条件和结论分别是另一个命题的________和________,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的__________.
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理.
阅读课本“议一议”,完成下面问题:
结论
条件
逆命题
归纳总结
例2. 说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形.
(2)两直线平行,同旁内角互补.
(3)如果ab=0,那么a=0,b=0.
经典例题
解:
(1)多边形是四边形.
原命题是真命题,而逆命题是假命题.
(2)同旁内角互补,两直线平行.
原命题与逆命题同为真命题.
(3)如果a=0,b=0,那么ab=0.
原命题是假命题,而逆命题是真命题.
经典例题
这节课我们学习了勾股定理及逆定理的证明方法,并结合数学和生活中的例子了解逆命题的概念,会识别两个互逆命题,知道,原命题成立,其逆命题不一定成立.
课堂小结
见《课堂达标卷》
课堂检测
课本17页 习题1.5 第1,3题
课后作业
2 直角三角形
第1课时
版 本:北京师范大学出版社
章 节:八年级下册第一章三角形的证明《直角三角形》(第1课时)
1.通过课本“想一想”会说出直角三角形的性质,并能解决相关问题.
2.通过例题证明,会说出直角三角形的判定方法,并能解决相关问题.
3.认识互逆命题、逆命题、互逆定理等概念,会说出一个命题的逆命题,并判断其真假.
学习目标
定理:有两个角互余的三角形是直角三角形.
定理:直角三角形的两个锐角互余.
(2)如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
(1)直角三角形的两个锐角又怎样的关系?为什么?
新知导入
算一算,猜一猜
已知在△ABC中,AB=c,BC=a,AC=b,
(1)填表:
a b c a2+b2与c2关系 三角形形状
3 4 5 ________ ______________
5 12 13 ________ ______________
8 15 17 ________ ______________
=
=
=
直角三角形
直角三角形
直角三角形
学习新知
图1 图2
(2)已知:如图1,在△ABC中,AB 2+AC 2=BC 2.
求证:△ABC是直角三角形.
学习新知
证明:如图2,作Rt△A′B′C′,使∠A′=90°,A′B′=AB,A′C′=AC,
则A′B′2+A′C′2=B′C′2(勾股定理).
∵AB2+AC2=BC2,
∴BC2=B′C′2.∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS).
∴∠A=∠A′=90°(全等三角形的对应角相等).
因此,△ABC是直角三角形.
学习新知
定理:
如果三角形两边的平方和等于第三边的平方,
那么这个三角形是________三角形.
直角
归纳总结
例1 如图所示,已知AB=4,BC=12,CD=13,DA=3,AB⊥AD,判断BC⊥BD是否成立,简述你的理由.
经典例题
解:BC⊥BD成立.理由如下:
在Rt△ABD中,∠BAD=90°,BD2=AB2+AD2=42+32=25.
又BD>0,
∴BD=5.
∵BD2+BC2=52+122=169=132=CD2,
∴∠DBC=90°,
∴BC⊥BD.
经典例题
勾股定理的逆定理 如果三角形两边的平方和等于第三边的平方,
那么这个三角形是直角三角形.
观察上面两个命题,它们的条件和结论之间有怎样的关系
在前面的学习中还有类似的命题吗
勾股定理的条件是第二个定理的结论,结论是第二个定理的条件..
勾股定理 在直角三角形中,两直角边的平方和等于斜边的平方.
想一想
1.如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角;
2.如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎;
3.一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等;
上面每组中两个命题的条件和结论也有类似的关系吗
与同伴交流.
想一想
在两个命题中,如果一个命题的条件和结论分别是另一个命题的________和________,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的__________.
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理.
阅读课本“议一议”,完成下面问题:
结论
条件
逆命题
归纳总结
例2. 说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形.
(2)两直线平行,同旁内角互补.
(3)如果ab=0,那么a=0,b=0.
经典例题
解:
(1)多边形是四边形.
原命题是真命题,而逆命题是假命题.
(2)同旁内角互补,两直线平行.
原命题与逆命题同为真命题.
(3)如果a=0,b=0,那么ab=0.
原命题是假命题,而逆命题是真命题.
经典例题
这节课我们学习了勾股定理及逆定理的证明方法,并结合数学和生活中的例子了解逆命题的概念,会识别两个互逆命题,知道,原命题成立,其逆命题不一定成立.
课堂小结
见《课堂达标卷》
课堂检测
课本17页 习题1.5 第1,3题
课后作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
