北师大版八年级数学下册 1.2直角三角形全等的判定 第2课时 课件(共21页)
文档属性
| 名称 | 北师大版八年级数学下册 1.2直角三角形全等的判定 第2课时 课件(共21页) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 20:34:58 | ||
图片预览




文档简介
(共21张PPT)
课程讲授
新知导入
随堂练习
课堂小结
第2课时 直角三角形全等的判定
第一章 三角形的证明
1.2 直角三角形
知识要点
1.直角三角形全等的判定
2.直角三角形全等的应用
新知导入
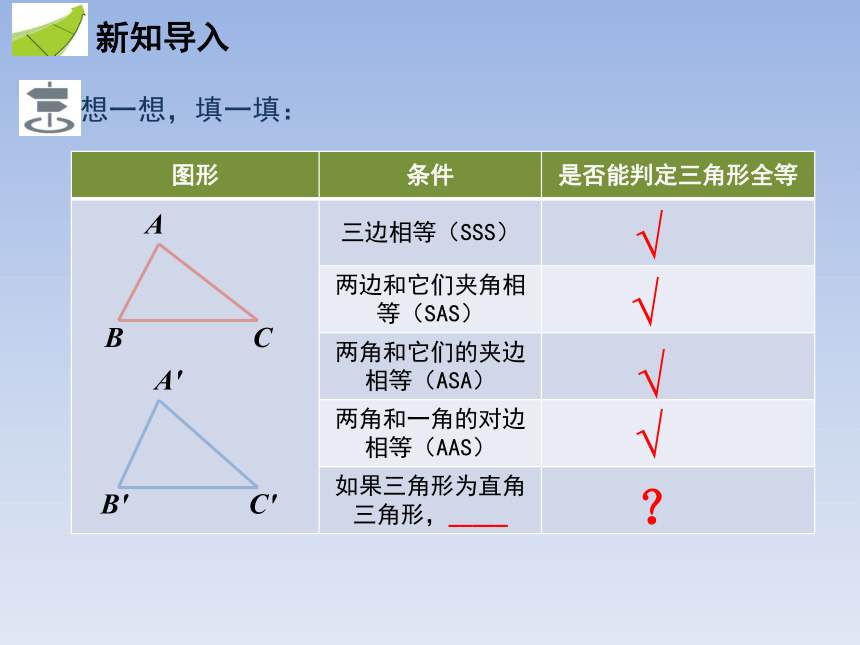
想一想,填一填:
图形 条件 是否能判定三角形全等
三边相等(SSS)
两边和它们夹角相等(SAS)
两角和它们的夹边相等(ASA)
两角和一角的对边相等(AAS)
如果三角形为直角三角形,_____
A
B
C
A'
B'
C'
√
√
?
√
√
课程讲授
1
直角三角形全等的判定
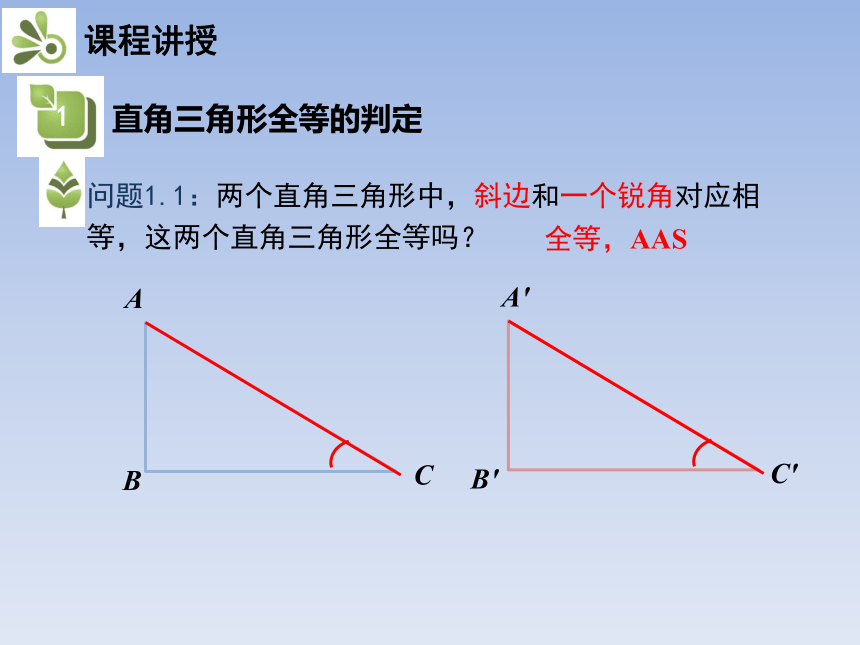
问题1.1:两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,AAS
课程讲授
1
直角三角形全等的判定
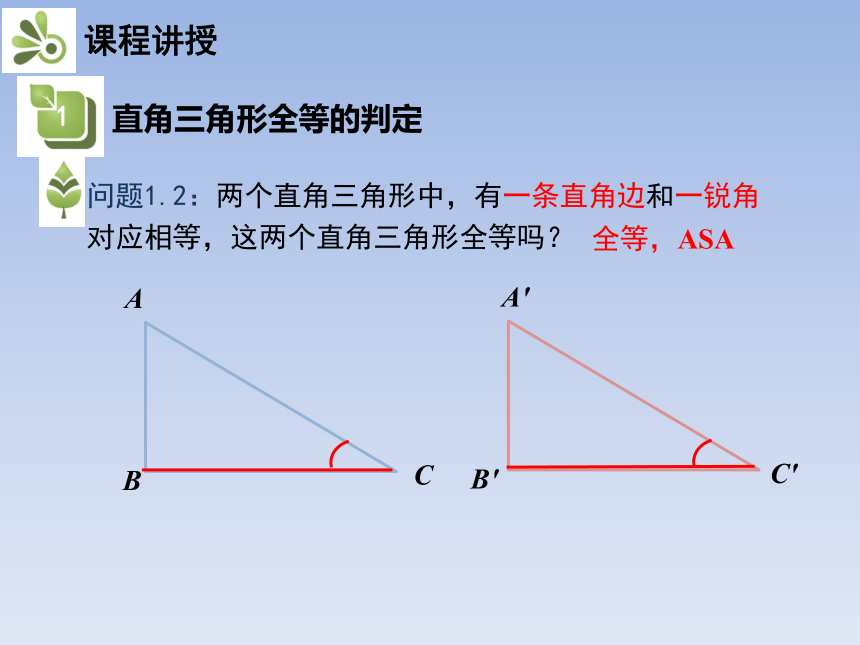
问题1.2:两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,ASA
课程讲授
1
直角三角形全等的判定
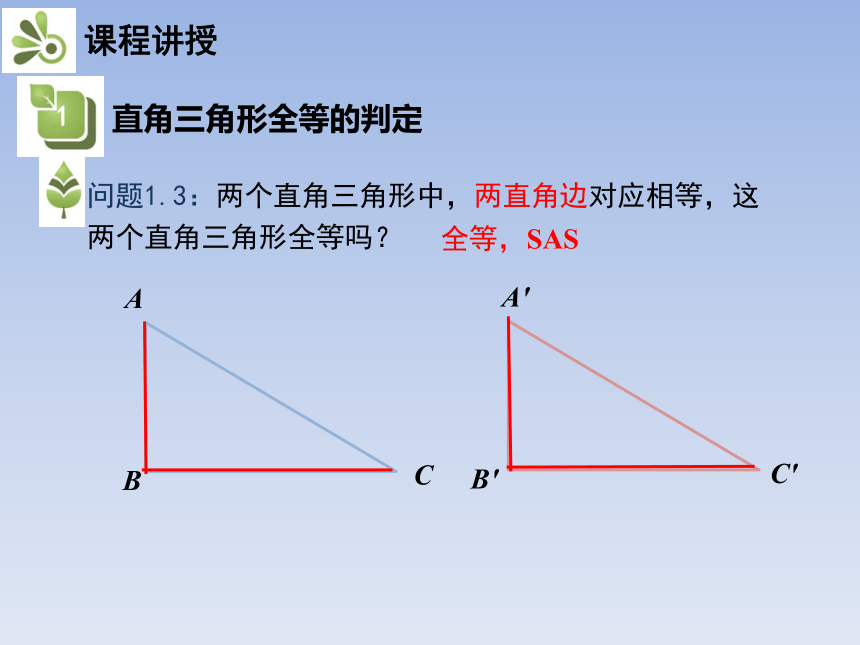
问题1.3:两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,SAS
课程讲授
1
直角三角形全等的判定
问题2:任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′,使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们能重合吗?
A
B
C
课程讲授
1
直角三角形全等的判定
A
B
C
作法:(1)先画∠MCN=90°,
(2)在射线C′M上截取B′C′=BC,
(3)以点B′为圆心,AB为半径画弧,交射线C′N于A′,
(4)连接A′B′.
C'
M
N
B'
A'
想一想:从中我们可以得到什么规律?
课程讲授
1
直角三角形全等的判定
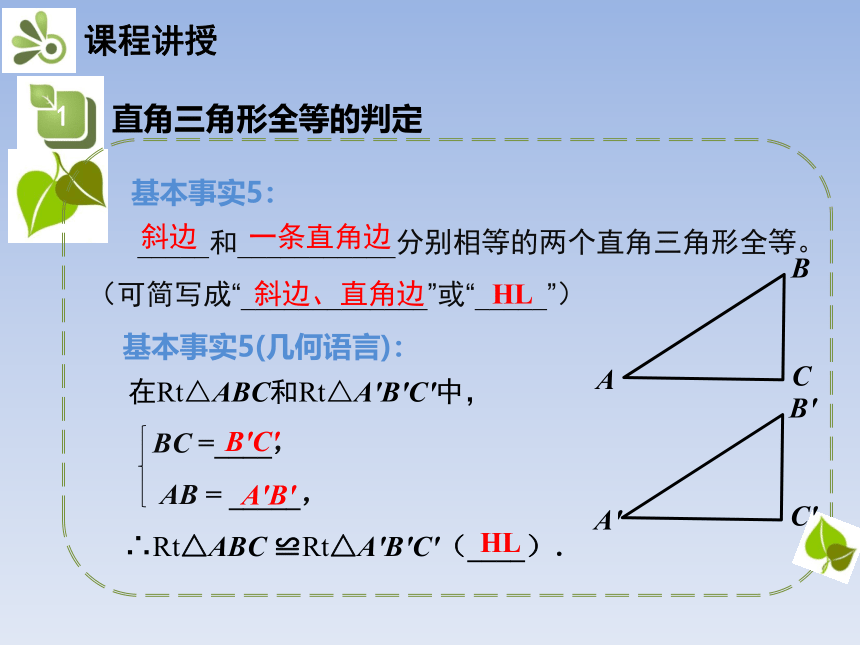
基本事实5:
_____和___________分别相等的两个直角三角形全等。(可简写成“_____________”或“_____”)
基本事实5(几何语言):
在Rt△ABC和Rt△A'B'C'中,
BC =____,
AB = _____,
∴Rt△ABC ≌Rt△A'B'C'(____).
A
B
C
A'
B'
C'
一条直角边
斜边
B'C'
A'B'
斜边、直角边
HL
HL
课程讲授
1
直角三角形全等的判定
例 如图,AC⊥BC, BD⊥AD,垂足分别为C,D , AC﹦BD,求证:BC﹦AD.
A
B
C
D
证明: ∵ AC⊥BC, BD⊥AD,
∴∠C与∠D都是直角.
在 Rt△ABC 和Rt△BAD 中,
AB=BA,
AC=BD .
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
课程讲授
1
直角三角形全等的判定
练一练:如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等,以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
课程讲授
2
直角三角形全等的应用
例 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
课程讲授
2
直角三角形全等的应用
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF ,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF
(全等三角形对应角相等).
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
课程讲授
2
直角三角形全等的应用
归纳:“HL”是判断两个直角三角形全等的简便方法,对于一般的三角形不成立,在使用时要注意其应用的范围.同时,利用“HL”还能说明两直线的位置关系,在实际解题过程中要结合实际灵活运用.
课程讲授
练一练:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么下列各条件中,不能使Rt△ABC和Rt△A′B′C′全等的是( )
A.AB=A′B′=5,BC=B′C′=3
B.AB=B′C′=5,∠A=∠B′=40°
C.AC=A′C′=5,BC=B′C′=3
D.AC=A′C′=5,∠A=∠A′=40°
B
2
直角三角形全等的应用
B
A
C
B'
A'
C'
随堂练习
1.下列条件:
①两条直角边对应相等;
②斜边和一锐角对应相等;
③斜边和一直角边对应相等;
④直角边和一锐角对应相等.
以上能判定两直角三角形全等的个数有( )
A.1个 B.2个
C.3个 D.4个
D
随堂练习
2.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点 E ,AD、CE交于点H,已知EH=EB=3,AE=4, 则 CH的长为( )
A.1 B.2 C.3 D.4
A
A
B
C
E
D
H
随堂练习
3.如图,在△ABC中,∠C=90°,DE⊥AB于点E,DE=DC,若AC=6,则AD+DE等于( )
A.7 B.6 C.5 D.4
B
随堂练习
4.如图,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,且OB=OC,有下列结论:
①∠1=∠2;
②△ADO≌△AEO;
③△BOD≌△COE;
④图中有四组三角形全等.
其中正确的个数有______个.
2
随堂练习
5.如图,在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.
求证:△EBC≌△DCB.
A
B
C
E
D
证明: ∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
CE=BD,
BC=CB .
∴Rt△EBC≌Rt△DCB (HL).
课堂小结
直角三角形全等的判定
内容
斜边和一条直角边分别相等的两个直角三角形全等.(简写成“斜边,直角边”或“HL”)
应用
1.使用的前提条件是在直角三角形中
2.遇到直角三角形全等问题,优先考虑“HL”
3.使用时只须找除直角外的两个条件即可(两个条件中至少有一个条件是一对对应边相等)
课程讲授
新知导入
随堂练习
课堂小结
第2课时 直角三角形全等的判定
第一章 三角形的证明
1.2 直角三角形
知识要点
1.直角三角形全等的判定
2.直角三角形全等的应用
新知导入
想一想,填一填:
图形 条件 是否能判定三角形全等
三边相等(SSS)
两边和它们夹角相等(SAS)
两角和它们的夹边相等(ASA)
两角和一角的对边相等(AAS)
如果三角形为直角三角形,_____
A
B
C
A'
B'
C'
√
√
?
√
√
课程讲授
1
直角三角形全等的判定
问题1.1:两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,AAS
课程讲授
1
直角三角形全等的判定
问题1.2:两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,ASA
课程讲授
1
直角三角形全等的判定
问题1.3:两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?
A
B
C
A'
B'
C'
全等,SAS
课程讲授
1
直角三角形全等的判定
问题2:任意画出一个Rt△ABC,使∠C=90°.再画一个Rt△A ′B ′C ′,使∠C′=90 °,B′C′=BC,A ′B ′=AB,把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们能重合吗?
A
B
C
课程讲授
1
直角三角形全等的判定
A
B
C
作法:(1)先画∠MCN=90°,
(2)在射线C′M上截取B′C′=BC,
(3)以点B′为圆心,AB为半径画弧,交射线C′N于A′,
(4)连接A′B′.
C'
M
N
B'
A'
想一想:从中我们可以得到什么规律?
课程讲授
1
直角三角形全等的判定
基本事实5:
_____和___________分别相等的两个直角三角形全等。(可简写成“_____________”或“_____”)
基本事实5(几何语言):
在Rt△ABC和Rt△A'B'C'中,
BC =____,
AB = _____,
∴Rt△ABC ≌Rt△A'B'C'(____).
A
B
C
A'
B'
C'
一条直角边
斜边
B'C'
A'B'
斜边、直角边
HL
HL
课程讲授
1
直角三角形全等的判定
例 如图,AC⊥BC, BD⊥AD,垂足分别为C,D , AC﹦BD,求证:BC﹦AD.
A
B
C
D
证明: ∵ AC⊥BC, BD⊥AD,
∴∠C与∠D都是直角.
在 Rt△ABC 和Rt△BAD 中,
AB=BA,
AC=BD .
∴ Rt△ABC≌Rt△BAD (HL).
∴ BC﹦AD.
课程讲授
1
直角三角形全等的判定
练一练:如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等,以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
课程讲授
2
直角三角形全等的应用
例 如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
课程讲授
2
直角三角形全等的应用
解:在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF ,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF
(全等三角形对应角相等).
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
课程讲授
2
直角三角形全等的应用
归纳:“HL”是判断两个直角三角形全等的简便方法,对于一般的三角形不成立,在使用时要注意其应用的范围.同时,利用“HL”还能说明两直线的位置关系,在实际解题过程中要结合实际灵活运用.
课程讲授
练一练:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,那么下列各条件中,不能使Rt△ABC和Rt△A′B′C′全等的是( )
A.AB=A′B′=5,BC=B′C′=3
B.AB=B′C′=5,∠A=∠B′=40°
C.AC=A′C′=5,BC=B′C′=3
D.AC=A′C′=5,∠A=∠A′=40°
B
2
直角三角形全等的应用
B
A
C
B'
A'
C'
随堂练习
1.下列条件:
①两条直角边对应相等;
②斜边和一锐角对应相等;
③斜边和一直角边对应相等;
④直角边和一锐角对应相等.
以上能判定两直角三角形全等的个数有( )
A.1个 B.2个
C.3个 D.4个
D
随堂练习
2.如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点 E ,AD、CE交于点H,已知EH=EB=3,AE=4, 则 CH的长为( )
A.1 B.2 C.3 D.4
A
A
B
C
E
D
H
随堂练习
3.如图,在△ABC中,∠C=90°,DE⊥AB于点E,DE=DC,若AC=6,则AD+DE等于( )
A.7 B.6 C.5 D.4
B
随堂练习
4.如图,CD⊥AB,BE⊥AC,垂足分别为点D,E,BE与CD相交于点O,且OB=OC,有下列结论:
①∠1=∠2;
②△ADO≌△AEO;
③△BOD≌△COE;
④图中有四组三角形全等.
其中正确的个数有______个.
2
随堂练习
5.如图,在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.
求证:△EBC≌△DCB.
A
B
C
E
D
证明: ∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
CE=BD,
BC=CB .
∴Rt△EBC≌Rt△DCB (HL).
课堂小结
直角三角形全等的判定
内容
斜边和一条直角边分别相等的两个直角三角形全等.(简写成“斜边,直角边”或“HL”)
应用
1.使用的前提条件是在直角三角形中
2.遇到直角三角形全等问题,优先考虑“HL”
3.使用时只须找除直角外的两个条件即可(两个条件中至少有一个条件是一对对应边相等)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
