八年级数学下册《9.2反比例函数的图象与性质(3)》课件 苏科版
文档属性
| 名称 | 八年级数学下册《9.2反比例函数的图象与性质(3)》课件 苏科版 |  | |
| 格式 | zip | ||
| 文件大小 | 330.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-31 17:20:00 | ||
图片预览




文档简介
课件11张PPT。初中数学八年级下册
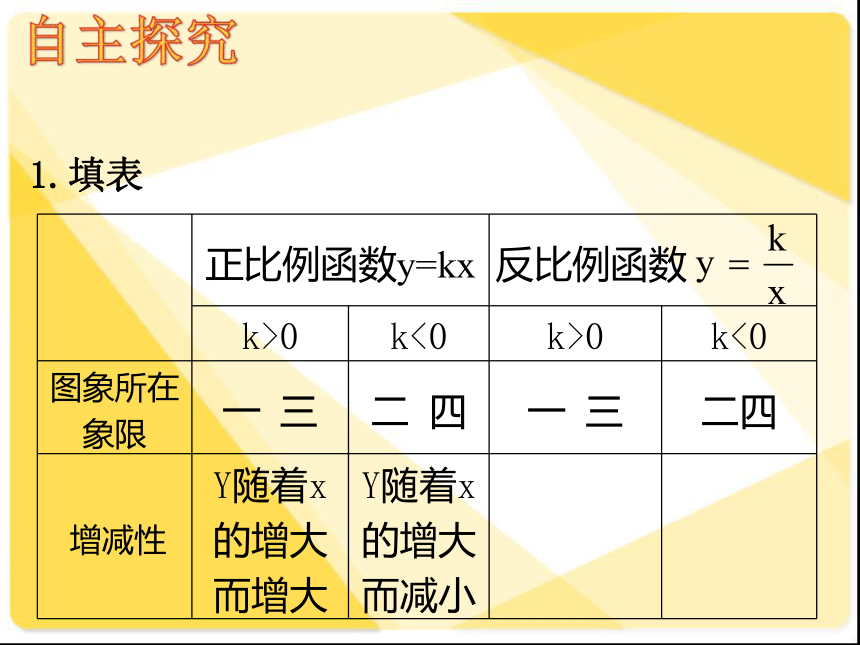
(苏科版)9.2 反比例函数的图象与性质(3)1.填表2.老师给出一个函数,甲、乙各指出这
个函数的一个性质:
甲:第一、三象限有它的图象;
乙:在每个象限内,y随x的增大而
减小.
请你写出一个满足上述性质的函数关系式
.3.点(-2,y1)(-1,y2)(1,y3)在反比例函数 的图象上,比较y1、y2、y3的大小.
思考:比较y1、y2、y3的大小有哪些方法?
代人法、图象法、增减性法例1:如图,是反比例函数 的图象的一支.
函数图象的另一支在第几象限?
求常数m的取值范围.
(3)点A(-3,y1)、B(-1,y2)、C(2,y3)都在这个反比例函数的图象上,比较y1、y2和y3的大小. 分析: 由于反比例函数图象的一支在第一象限,所以另一支在第三象限,显然2-m﹥0,由此得到m的取值范围,由于反比例函数的自变量x的取值范围是x≠0,所以其图象是分段的,不连续的,在讨论函数值的大小问题时,我们必须分象限来进行讨论.问题3的解决有如下几种方法:代人法,即代人到解析式中求解后进行比较;图象法,利用图象观察、比较得出;增减性法,利用反比例函数图象的增减性在每个分支上进行分析、解决.1.对于反比例函数y = x(k)(k>0),当x1 < 0< x2(1)求n的取值范围.
(2)点(2,a)、(-1,b)、(-2,c)都在这个反比例函数图象上,比较a、b、c的大小. 3.已知反比例函数 与一次函数y=mx+b的图象交于P(-2,1)和Q(1,n)两点.
(1) 求k、n的值;
(2) 求一次函数y=mx+b的解析式.
(3) 求△POQ的面积.4. 已知反比例函数y1 = 和一次函数 y2=kx+2的图象都过点P(a,2a).
(1) 求a与k的值;
(2) 在同一坐标系中画出这两个函数的图象;
(3) 若两函数图象的另一个交点是Q(0.5,4),利用图象指出:当x为何值时,有y1﹥y2? 再见 谢谢合作
(苏科版)9.2 反比例函数的图象与性质(3)1.填表2.老师给出一个函数,甲、乙各指出这
个函数的一个性质:
甲:第一、三象限有它的图象;
乙:在每个象限内,y随x的增大而
减小.
请你写出一个满足上述性质的函数关系式
.3.点(-2,y1)(-1,y2)(1,y3)在反比例函数 的图象上,比较y1、y2、y3的大小.
思考:比较y1、y2、y3的大小有哪些方法?
代人法、图象法、增减性法例1:如图,是反比例函数 的图象的一支.
函数图象的另一支在第几象限?
求常数m的取值范围.
(3)点A(-3,y1)、B(-1,y2)、C(2,y3)都在这个反比例函数的图象上,比较y1、y2和y3的大小. 分析: 由于反比例函数图象的一支在第一象限,所以另一支在第三象限,显然2-m﹥0,由此得到m的取值范围,由于反比例函数的自变量x的取值范围是x≠0,所以其图象是分段的,不连续的,在讨论函数值的大小问题时,我们必须分象限来进行讨论.问题3的解决有如下几种方法:代人法,即代人到解析式中求解后进行比较;图象法,利用图象观察、比较得出;增减性法,利用反比例函数图象的增减性在每个分支上进行分析、解决.1.对于反比例函数y = x(k)(k>0),当x1 < 0< x2
(2)点(2,a)、(-1,b)、(-2,c)都在这个反比例函数图象上,比较a、b、c的大小. 3.已知反比例函数 与一次函数y=mx+b的图象交于P(-2,1)和Q(1,n)两点.
(1) 求k、n的值;
(2) 求一次函数y=mx+b的解析式.
(3) 求△POQ的面积.4. 已知反比例函数y1 = 和一次函数 y2=kx+2的图象都过点P(a,2a).
(1) 求a与k的值;
(2) 在同一坐标系中画出这两个函数的图象;
(3) 若两函数图象的另一个交点是Q(0.5,4),利用图象指出:当x为何值时,有y1﹥y2? 再见 谢谢合作
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
