人教版八年级数学下册第18章《平行四边形》单元测试(word版含答案)
文档属性
| 名称 | 人教版八年级数学下册第18章《平行四边形》单元测试(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 637.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-08 22:25:07 | ||
图片预览



文档简介
2021-2022学年人教版八年级数学下册
第18章《平行四边形》单元测试
一、单选题(共30分)
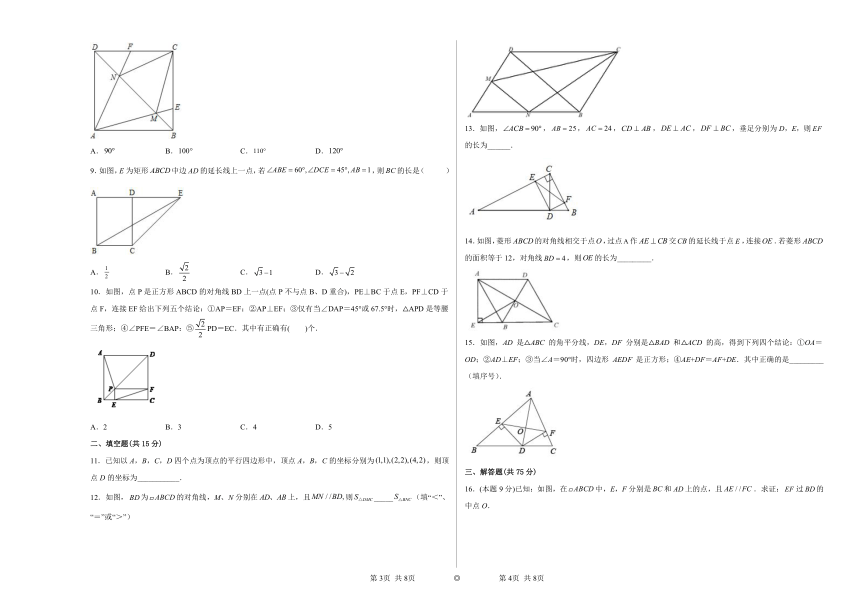
1.如图,中,点D、E、F分别为边的中点,则下列关于线段和之间关系的说法中正确的是( )
A. B.
C.和互相平分 D.以上答案都不对
2.如图,在平行四边形ABCD中,∠ODA=90°,AC=10,BD=6,则AD的长为( )
A.4 B.5 C.6 D.8
3.如图,AD和BE分别是△ABC的中线和角平分线,AD⊥BE,垂足为点F,且G、E为AC的三等分点,若BE=4,则BF的长为( )
A.2 B.3 C.4 D.5
4.如图,在平行四边形中,,为对角线,,边上的高为4,则图中阴影部分的面积为( )
A.3 B.6 C.12 D.24
5.如图,将一个边长分别为4,8的矩形纸片折叠,使点C与点A重合,则折痕的长是( ).
A. B. C. D.
6.如图,P是矩形的边上一个动点,矩形的两条边的长分别为3和4,那么点P到矩形的两条对角线和的距离之和是( )
A. B. C. D.无法确定
7.如图,把菱形ABCD向右平移至DCEF的位置,作EG⊥AB,垂足为G,EG与CD相交于点K,GD的延长线交EF于点H,连接DE,则下列结论:①BG=AB+HF;②DG=DE;③∠DHE=∠BAD;④∠B=∠DEF,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
8.如图,E、F分别为正方形中边上的点,且分别交对角线于点M、N,则的大小是( )
A. B. C. D.
9.如图,E为矩形中边的延长线上一点,若,则的长是( )
A. B. C. D.
10.如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤PD=EC.其中有正确有( )个.
A.2 B.3 C.4 D.5
二、填空题(共15分)
11.已知以A,B,C,D四个点为顶点的平行四边形中,顶点A,B,C的坐标分别为,则顶点D的坐标为___________.
12.如图,为的对角线,M、N分别在上,且则_____(填“<”、“=”或“>”)
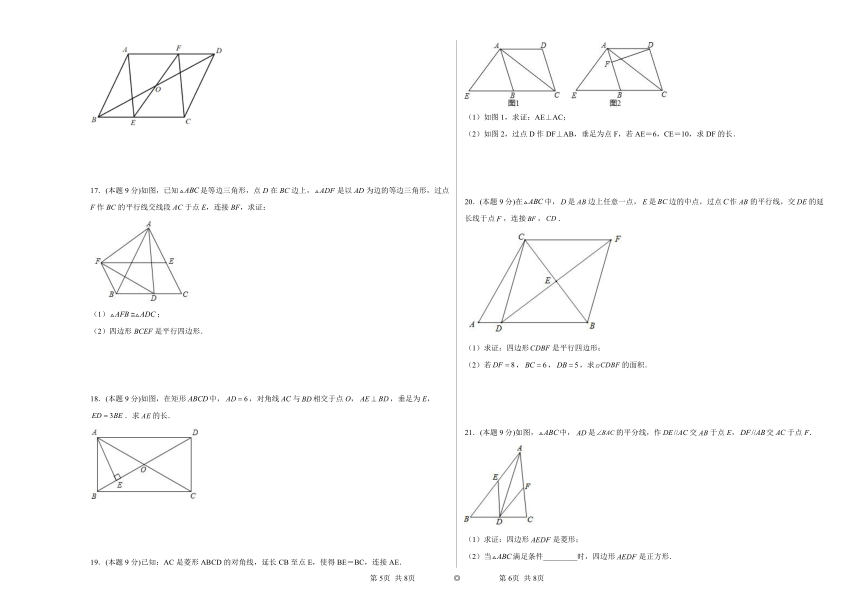
13.如图,,,,,,,垂足分别为D,E,则的长为______.
14.如图,菱形的对角线相交于点,过点作交的延长线于点,连接.若菱形的面积等于12,对角线,则的长为_________.
15.如图,AD 是△ABC 的角平分线,DE,DF 分别是△BAD 和△ACD 的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形 AEDF 是正方形;④AE+DF=AF+DE.其中正确的是_________(填序号).
三、解答题(共75分)
16.(本题9分)已知:如图,在中,E,F分别是和上的点,且.求证:过的中点O.
17.(本题9分)如图,已知是等边三角形,点D在BC边上,是以AD为边的等边三角形,过点F作BC的平行线交线段AC于点E,连接BF,求证:
(1);
(2)四边形BCEF是平行四边形.
18.(本题9分)如图,在矩形中,,对角线与相交于点O,,垂足为E,.求的长.
19.(本题9分)已知:AC是菱形ABCD的对角线,延长CB至点E,使得BE=BC,连接AE.
(1)如图1,求证:AE⊥AC;
(2)如图2,过点D作DF⊥AB,垂足为点F,若AE=6,CE=10,求DF的长.
20.(本题9分)在中,是边上任意一点,是边的中点,过点作的平行线,交的延长线于点,连接,.
(1)求证:四边形是平行四边形;
(2)若,,,求的面积.
21.(本题9分)如图,中,是的平分线,作交于点E,交于点F.
(1)求证:四边形是菱形;
(2)当满足条件_________时,四边形是正方形.
22.(本题10分)在矩形中,点F在延长线上,且,M为边上一点,N为的中点,点E在直线上(点E、C不重合).
(1)如图1,若,点M、A重合,E为的中点,试探究与的位置关系及的值,并证明你的结论;
(2)如图2,且若,点M、A不重合,,你在(1)中得到的两个结论是否成立,若成立,加以证明;若不成立,请说明理由;
(3)如图3,若点M、A不重合,,你在(1)中得到的结论两个是否成立,请直接写出你的结论.
23.(本题11分)四边形为正方形,点为线段上一点,连接,过点作,交射线于点,以、为邻边作矩形,连接.
(1)如图,求证:矩形是正方形;
(2)若,求的长度;
(3)当线段与正方形的某条边的夹角是30°时,直接写出的度数.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案
1.C
2.A
3.B
4.C
5.D
6.A
7.C
8.B
9.C
10.D
11.
12.=
13.
14.3
15.②③④.
16.
如图,连接
四边形是平行四边,
,,
,
四边形是平行四边形,
,
,
即,
四边形是平行四边形,
与互相平分,
是的中点,
过的中点.
17.
(1)∵和都是等边三角形,
∴,
,即,
在和中,,
∴;
(2)∵,
∴,
又∵,
∴,
∴,
又∵,
∴四边形BCEF是平行四边形.
18.
解:∵四边形是矩形,
∴OB=OD,OA=OC,AC=BD,.
∴,
∵,
∴.
又∵,
∴.
∴,
即是等边三角形.
∴.
∴.
在中,
∵,,
∴.
19.
(1)证明:连接BD,交AC于点O,
∵四边形ABCD是菱形
∴AO=CO,∠BOC=90°
∵AO=CO,BE=BC
∴OB=AE,BD∥AE,且∠BOC=90°
∴∠EAC=∠BOC=90°
∴AE⊥AC
(2)连接BD,
∵∠EAC=90°,AE=6,CE=10,
∴AC==8
∵AE=6,CE=10,BE=BC,AE=2BO
∴BO=3=DO,BC=5=AB
∵S菱形ABCD=DF×AB=AC×BD,
∴5DF=×6×8
∴DF=
20.
(1)是边的中点,
,
,
,
在和中,,
,
,
四边形的对角线互相平分,
四边形是平行四边形;
(2),,
,,
,
,
是直角三角形,
,
平行四边形是菱形,
的面积为.
21.
(1)证明:∵DEAC交AB于点E,DFAB交AC于点F,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∵AD是∠BAC的角平分线,
∴∠EAD=∠FAD,
∴∠ADF=∠FAD,
∴FA=FD,
∴四边形AEDF是菱形(有一组邻边相等的平行四边形是菱形);
(2)解:当△ABC是直角三角形,∠BAC=90°时,四边形AEDF是正方形,
理由:∵△ABC是直角三角形,∠BAC=90°,
由(1)知四边形AEDF是菱形,
∴四边形AEDF是正方形(有一个角是直角的菱形是正方形).
22.
解:(1)BN与NE的位置关系是BN⊥NE,=,
证明:如图,过点E作EG⊥AF于G,则∠EGN=90°,
∵矩形ABCD中,AB=BC,
∴矩形ABCD为正方形,
∴AB=AD=CD,∠A=∠ADC=∠DCB=90°,
∴EG∥CD,∠EGN=∠A,∠CDF=90°,
∵E为CF的中点,EG∥CD,
∴GF=DG=DF=CD,
∴GE=CD,
∵N为MD(AD)的中点,
∴AN=ND=AD=CD,
∴GE=AN,NG=ND+DG=ND+AN=AD=AB,
∴△NGE≌△BAN,
∴∠1=∠2,
∵∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠BNE=90°,
∴BN⊥NE,
∵∠CDF=90°,CD=DF,
可得∠F=∠FCD=45°,
,
于是.
(2)在(1)中得到的两个结论均成立.
证明:如图,延长BN交CD的延长线于点G,连接BE、GE,过E作EH⊥CE, 交CD于点H,
∵四边形ABCD是矩形,
∴AB∥CG,
∴∠MBN=∠DGN,∠BMN=∠GDN,
∵N为MD的中点,
∴MN=DN,
∴△BMN≌△GDN,
∴MB=DG,BN=GN,
∵BN=NE,
∴BN=NE=GN,
∴∠BEG=90°,
∵EH⊥CE,
∴∠CEH=90°,
∴∠BEG=∠CEH,
∴∠BEC=∠GEH,
由(1)得∠DCF=45°,
∴∠CHE=∠HCE=45°,
∴EC=EH,∠EHG=135°,
∵∠ECB=∠DCB+∠HCE=135°,
∴∠ECB=∠EHG,
∴△ECB≌△EHG,
∴EB=EG,CB=HG,
∵BN=NG,
∴BN⊥NE,
∵BM=DG=HG-HD=BC-HD=CD-HD=CH=CE,
∴ ;
(3)BN⊥NE,不一定等于,
证明:可以延长BN交CD的延长线于点G,连接BE、GE,过E作EH⊥CE,H在DC的延长线上, GE交AD于点Q,
同(2)可以证得:△BMN≌△GDN 则BN=NG=NE,
则△BEG是直角三角形,∠BEG=90°,
与(2)相同,可证:△ECB≌△HEG,
∴EB=EG,CB=CG,
∵BN=NG,
∴BN⊥NE,
同(2)可得:GQ=CE≠DG=BM,
故不一定等于(只有当Q与D重合时才相等).
23.
解:(1)证明:过作于点,于点,如图:
∵四边形为正方形
∴
∴
∵
∴
∵
∵
∴
∴在和
∴
∴
∴矩形是正方形.
(2)如图:
∵由(1)可知,在中,
∴
∵
∴
∴与重合
∵四边形是正方形
∴.
(3)①当与的夹角为时,如图:
∵,
∴
∴
∴;
②当与的夹角为时,如图:
∵,
∴
∴
∵
∴.
∴综上所述, 或
故答案是:(1)证明见解析(2)(3)当与的夹角为时,;当与的夹角为时,
答案第1页,共2页
答案第1页,共2页
第18章《平行四边形》单元测试
一、单选题(共30分)
1.如图,中,点D、E、F分别为边的中点,则下列关于线段和之间关系的说法中正确的是( )
A. B.
C.和互相平分 D.以上答案都不对
2.如图,在平行四边形ABCD中,∠ODA=90°,AC=10,BD=6,则AD的长为( )
A.4 B.5 C.6 D.8
3.如图,AD和BE分别是△ABC的中线和角平分线,AD⊥BE,垂足为点F,且G、E为AC的三等分点,若BE=4,则BF的长为( )
A.2 B.3 C.4 D.5
4.如图,在平行四边形中,,为对角线,,边上的高为4,则图中阴影部分的面积为( )
A.3 B.6 C.12 D.24
5.如图,将一个边长分别为4,8的矩形纸片折叠,使点C与点A重合,则折痕的长是( ).
A. B. C. D.
6.如图,P是矩形的边上一个动点,矩形的两条边的长分别为3和4,那么点P到矩形的两条对角线和的距离之和是( )
A. B. C. D.无法确定
7.如图,把菱形ABCD向右平移至DCEF的位置,作EG⊥AB,垂足为G,EG与CD相交于点K,GD的延长线交EF于点H,连接DE,则下列结论:①BG=AB+HF;②DG=DE;③∠DHE=∠BAD;④∠B=∠DEF,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
8.如图,E、F分别为正方形中边上的点,且分别交对角线于点M、N,则的大小是( )
A. B. C. D.
9.如图,E为矩形中边的延长线上一点,若,则的长是( )
A. B. C. D.
10.如图,点P是正方形ABCD的对角线BD上一点(点P不与点B、D重合),PE⊥BC于点E,PF⊥CD于点F,连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③仅有当∠DAP=45°或67.5°时,△APD是等腰三角形;④∠PFE=∠BAP:⑤PD=EC.其中有正确有( )个.
A.2 B.3 C.4 D.5
二、填空题(共15分)
11.已知以A,B,C,D四个点为顶点的平行四边形中,顶点A,B,C的坐标分别为,则顶点D的坐标为___________.
12.如图,为的对角线,M、N分别在上,且则_____(填“<”、“=”或“>”)
13.如图,,,,,,,垂足分别为D,E,则的长为______.
14.如图,菱形的对角线相交于点,过点作交的延长线于点,连接.若菱形的面积等于12,对角线,则的长为_________.
15.如图,AD 是△ABC 的角平分线,DE,DF 分别是△BAD 和△ACD 的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形 AEDF 是正方形;④AE+DF=AF+DE.其中正确的是_________(填序号).
三、解答题(共75分)
16.(本题9分)已知:如图,在中,E,F分别是和上的点,且.求证:过的中点O.
17.(本题9分)如图,已知是等边三角形,点D在BC边上,是以AD为边的等边三角形,过点F作BC的平行线交线段AC于点E,连接BF,求证:
(1);
(2)四边形BCEF是平行四边形.
18.(本题9分)如图,在矩形中,,对角线与相交于点O,,垂足为E,.求的长.
19.(本题9分)已知:AC是菱形ABCD的对角线,延长CB至点E,使得BE=BC,连接AE.
(1)如图1,求证:AE⊥AC;
(2)如图2,过点D作DF⊥AB,垂足为点F,若AE=6,CE=10,求DF的长.
20.(本题9分)在中,是边上任意一点,是边的中点,过点作的平行线,交的延长线于点,连接,.
(1)求证:四边形是平行四边形;
(2)若,,,求的面积.
21.(本题9分)如图,中,是的平分线,作交于点E,交于点F.
(1)求证:四边形是菱形;
(2)当满足条件_________时,四边形是正方形.
22.(本题10分)在矩形中,点F在延长线上,且,M为边上一点,N为的中点,点E在直线上(点E、C不重合).
(1)如图1,若,点M、A重合,E为的中点,试探究与的位置关系及的值,并证明你的结论;
(2)如图2,且若,点M、A不重合,,你在(1)中得到的两个结论是否成立,若成立,加以证明;若不成立,请说明理由;
(3)如图3,若点M、A不重合,,你在(1)中得到的结论两个是否成立,请直接写出你的结论.
23.(本题11分)四边形为正方形,点为线段上一点,连接,过点作,交射线于点,以、为邻边作矩形,连接.
(1)如图,求证:矩形是正方形;
(2)若,求的长度;
(3)当线段与正方形的某条边的夹角是30°时,直接写出的度数.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案
1.C
2.A
3.B
4.C
5.D
6.A
7.C
8.B
9.C
10.D
11.
12.=
13.
14.3
15.②③④.
16.
如图,连接
四边形是平行四边,
,,
,
四边形是平行四边形,
,
,
即,
四边形是平行四边形,
与互相平分,
是的中点,
过的中点.
17.
(1)∵和都是等边三角形,
∴,
,即,
在和中,,
∴;
(2)∵,
∴,
又∵,
∴,
∴,
又∵,
∴四边形BCEF是平行四边形.
18.
解:∵四边形是矩形,
∴OB=OD,OA=OC,AC=BD,.
∴,
∵,
∴.
又∵,
∴.
∴,
即是等边三角形.
∴.
∴.
在中,
∵,,
∴.
19.
(1)证明:连接BD,交AC于点O,
∵四边形ABCD是菱形
∴AO=CO,∠BOC=90°
∵AO=CO,BE=BC
∴OB=AE,BD∥AE,且∠BOC=90°
∴∠EAC=∠BOC=90°
∴AE⊥AC
(2)连接BD,
∵∠EAC=90°,AE=6,CE=10,
∴AC==8
∵AE=6,CE=10,BE=BC,AE=2BO
∴BO=3=DO,BC=5=AB
∵S菱形ABCD=DF×AB=AC×BD,
∴5DF=×6×8
∴DF=
20.
(1)是边的中点,
,
,
,
在和中,,
,
,
四边形的对角线互相平分,
四边形是平行四边形;
(2),,
,,
,
,
是直角三角形,
,
平行四边形是菱形,
的面积为.
21.
(1)证明:∵DEAC交AB于点E,DFAB交AC于点F,
∴四边形AEDF是平行四边形,∠EAD=∠ADF,
∵AD是∠BAC的角平分线,
∴∠EAD=∠FAD,
∴∠ADF=∠FAD,
∴FA=FD,
∴四边形AEDF是菱形(有一组邻边相等的平行四边形是菱形);
(2)解:当△ABC是直角三角形,∠BAC=90°时,四边形AEDF是正方形,
理由:∵△ABC是直角三角形,∠BAC=90°,
由(1)知四边形AEDF是菱形,
∴四边形AEDF是正方形(有一个角是直角的菱形是正方形).
22.
解:(1)BN与NE的位置关系是BN⊥NE,=,
证明:如图,过点E作EG⊥AF于G,则∠EGN=90°,
∵矩形ABCD中,AB=BC,
∴矩形ABCD为正方形,
∴AB=AD=CD,∠A=∠ADC=∠DCB=90°,
∴EG∥CD,∠EGN=∠A,∠CDF=90°,
∵E为CF的中点,EG∥CD,
∴GF=DG=DF=CD,
∴GE=CD,
∵N为MD(AD)的中点,
∴AN=ND=AD=CD,
∴GE=AN,NG=ND+DG=ND+AN=AD=AB,
∴△NGE≌△BAN,
∴∠1=∠2,
∵∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠BNE=90°,
∴BN⊥NE,
∵∠CDF=90°,CD=DF,
可得∠F=∠FCD=45°,
,
于是.
(2)在(1)中得到的两个结论均成立.
证明:如图,延长BN交CD的延长线于点G,连接BE、GE,过E作EH⊥CE, 交CD于点H,
∵四边形ABCD是矩形,
∴AB∥CG,
∴∠MBN=∠DGN,∠BMN=∠GDN,
∵N为MD的中点,
∴MN=DN,
∴△BMN≌△GDN,
∴MB=DG,BN=GN,
∵BN=NE,
∴BN=NE=GN,
∴∠BEG=90°,
∵EH⊥CE,
∴∠CEH=90°,
∴∠BEG=∠CEH,
∴∠BEC=∠GEH,
由(1)得∠DCF=45°,
∴∠CHE=∠HCE=45°,
∴EC=EH,∠EHG=135°,
∵∠ECB=∠DCB+∠HCE=135°,
∴∠ECB=∠EHG,
∴△ECB≌△EHG,
∴EB=EG,CB=HG,
∵BN=NG,
∴BN⊥NE,
∵BM=DG=HG-HD=BC-HD=CD-HD=CH=CE,
∴ ;
(3)BN⊥NE,不一定等于,
证明:可以延长BN交CD的延长线于点G,连接BE、GE,过E作EH⊥CE,H在DC的延长线上, GE交AD于点Q,
同(2)可以证得:△BMN≌△GDN 则BN=NG=NE,
则△BEG是直角三角形,∠BEG=90°,
与(2)相同,可证:△ECB≌△HEG,
∴EB=EG,CB=CG,
∵BN=NG,
∴BN⊥NE,
同(2)可得:GQ=CE≠DG=BM,
故不一定等于(只有当Q与D重合时才相等).
23.
解:(1)证明:过作于点,于点,如图:
∵四边形为正方形
∴
∴
∵
∴
∵
∵
∴
∴在和
∴
∴
∴矩形是正方形.
(2)如图:
∵由(1)可知,在中,
∴
∵
∴
∴与重合
∵四边形是正方形
∴.
(3)①当与的夹角为时,如图:
∵,
∴
∴
∴;
②当与的夹角为时,如图:
∵,
∴
∴
∵
∴.
∴综上所述, 或
故答案是:(1)证明见解析(2)(3)当与的夹角为时,;当与的夹角为时,
答案第1页,共2页
答案第1页,共2页
